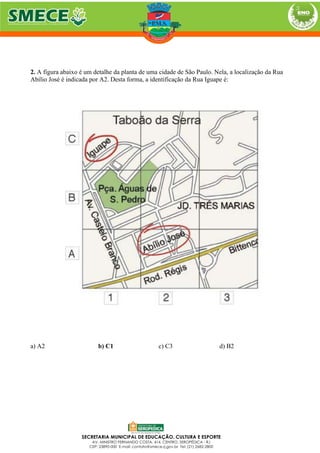
[1] O documento descreve os descritores de Matemática da Prova Brasil de 2013 para o 5o ano, incluindo habilidades de espaço e forma, grandezas e medidas, números e operações e tratamento da informação. [2] São fornecidos exemplos de questões para avaliar cada descritor. [3] Comentários discutem a importância de abordar a geometria em sala de aula para o desempenho nas provas.