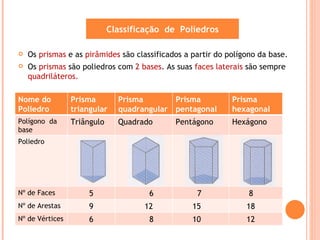
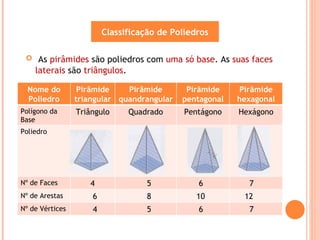
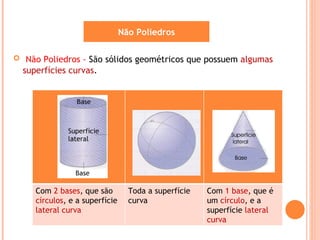
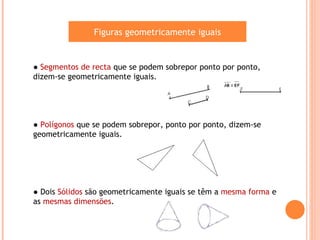
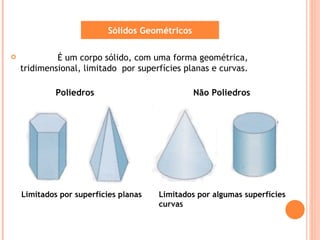
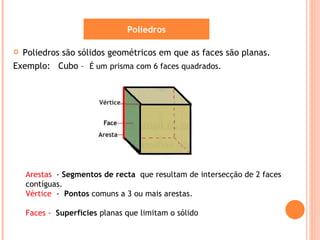
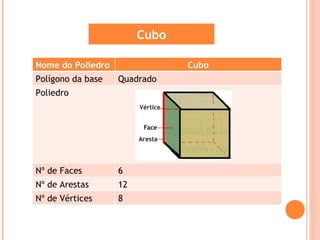
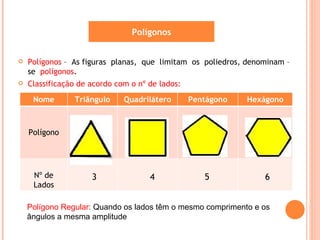
O documento descreve os principais tipos de sólidos geométricos, incluindo poliedros e não poliedros. Poliedros são sólidos com faces planas, como cubos e pirâmides, enquanto não poliedros têm algumas superfícies curvas. Vários sólidos são classificados e ilustrados com exemplos de suas faces, arestas e vértices.

1. SÓLIDOS GEOMÉTRICOS
Poliedros e não poliedros

2. As Formas existentes na Natureza e
os Sólidos Geométricos
 Todos os seres vivos e não vivos, que nos rodeiam, têm
formas geométricas próprias.
Sólidos Geométricos
Pirâmide
Cubo
Prisma
Podemos associar a forma do cristal de pirite ao cubo e a forma
do cristal de quartzo a um prisma hexagonal que termina em
pirâmide hexagonal.

3. Sólidos Geométricos
 É um corpo sólido, com uma forma geométrica,
tridimensional, limitado por superfícies planas e curvas.
Poliedros Não Poliedros
Limitados por superfícies planas Limitados por algumas superfícies
curvas

4. Poliedros
 Poliedros são sólidos geométricos em que as faces são planas.
Exemplo: Cubo – É um prisma com 6 faces quadrados.
Arestas - Segmentos de recta que resultam de intersecção de 2 faces
contíguas.
Vértice - Pontos comuns a 3 ou mais arestas.
Faces - Superfícies planas que limitam o sólido

5. Cubo
Nome do Poliedro Cubo
Polígono da base Quadrado
Poliedro
Nº de Faces 6
Nº de Arestas 12
Nº de Vértices 8

6. Polígonos
 Polígonos – As figuras planas, que limitam os poliedros, denominam –
se polígonos.
 Classificação de acordo com o nº de lados:
Nome Triângulo Quadrilátero Pentágono Hexágono
Polígono
Nº de 3 4 5 6
Lados
Polígono Regular: Quando os lados têm o mesmo comprimento e os
ângulos a mesma amplitude

7. Recta, Semi-recta, Segmento de Recta
O polígono da figura é o triângulo [ A B C]
● A, B, C, são vértices deste polígono
● [ AB], [ BC], [CA] são lados deste polígono,
segmentos de recta.
● Prolongando para ambos os lados, indefinidamente o lado [ AC], obtemos a
recta r ou recta AC.
● Prolongando para um dos lados, indefinidamente o lado [ AB], obtemos
a semi-recta AB. ou ● ( semi-recta com origem em A )
AB

8. Classificação de Poliedros
 Os prismas e as pirâmides são classificados a partir do polígono da base.
 Os prismas são poliedros com 2 bases. As suas faces laterais são sempre
quadriláteros.
Nome do Prisma Prisma Prisma Prisma
Poliedro triangular quadrangular pentagonal hexagonal
Polígono da Triângulo Quadrado Pentágono Hexágono
base
Poliedro
Nº de Faces 5 6 7 8
Nº de Arestas 9 12 15 18
Nº de Vértices 6 8 10 12

9. Classificação de Poliedros
 As pirâmides são poliedros com uma só base. As suas faces
laterais são triângulos.
Nome do Pirâmide Pirâmide Pirâmide Pirâmide
Poliedro triangular quandrangular pentagonal hexagonal
Polígono da Triângulo Quadrado Pentágono Hexágono
Base
Poliedro
Nº de Faces 4 5 6 7
Nº de Arestas 6 8 10 12
Nº de Vértices 4 5 6 7

10. Fórmula
Em qualquer poliedro:
Nº de Faces + Nº de Vértices = Nº de Arestas + 2

11. Poliedros com faces
geometricamente iguais
Tetraedro Cubo Octaedro Dodecaedro Icosaedro
( 4 faces ) ( 6 faces ) ( 8 faces ) ( 12 faces ) ( 20 faces )

12. Não Poliedros
 Não Poliedros - São sólidos geométricos que possuem algumas
superfícies curvas.
Com 2 bases, que são Toda a superfície Com 1 base, que é
círculos, e a superfície curva um círculo, e a
lateral curva superfície lateral
curva

13. Figuras geometricamente iguais
● Segmentos de recta que se podem sobrepor ponto por ponto,
dizem-se geometricamente iguais.
● Polígonos que se podem sobrepor, ponto por ponto, dizem-se
geometricamente iguais.
● Dois Sólidos são geometricamente iguais se têm a mesma forma e
as mesmas dimensões.