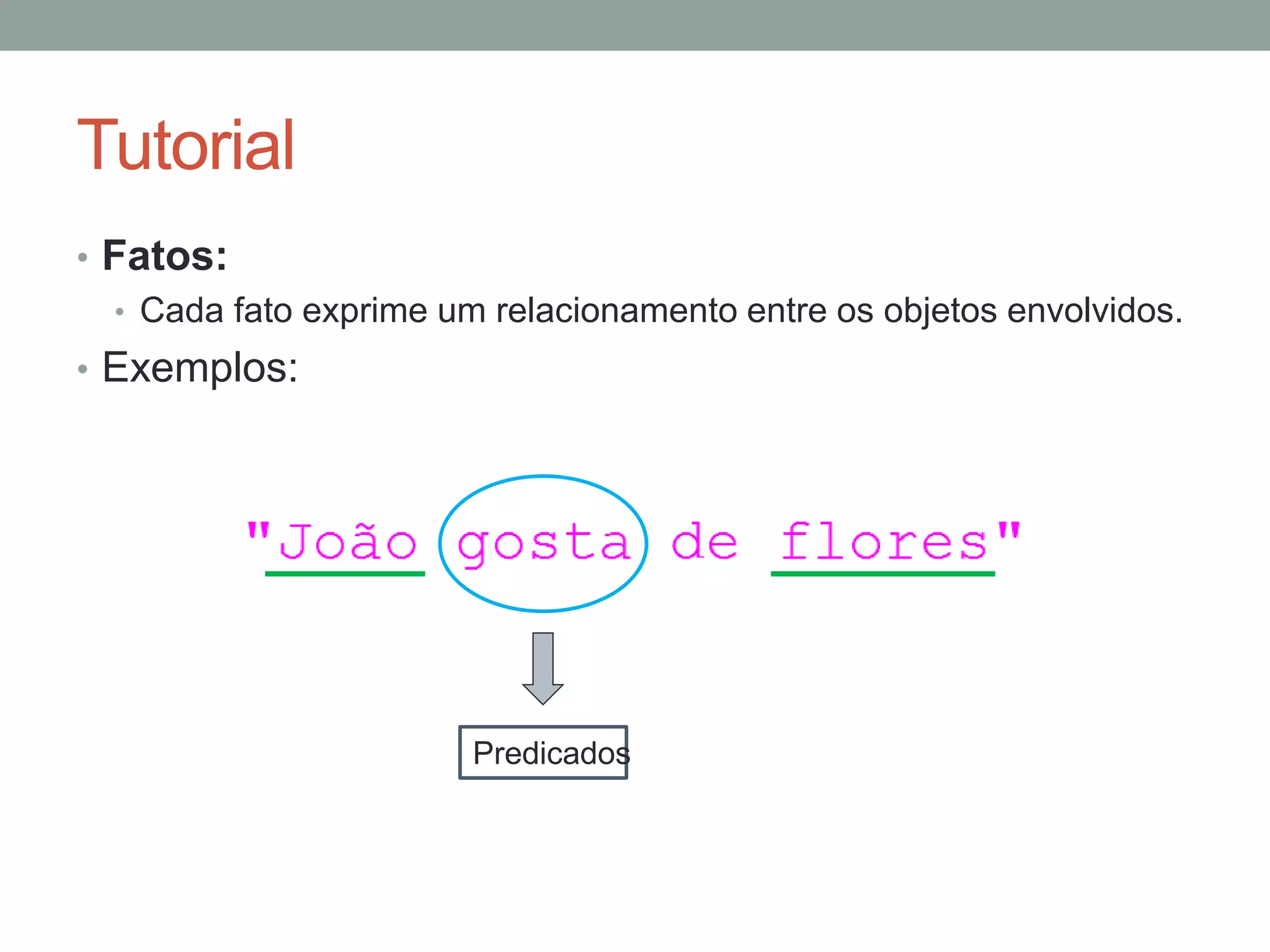
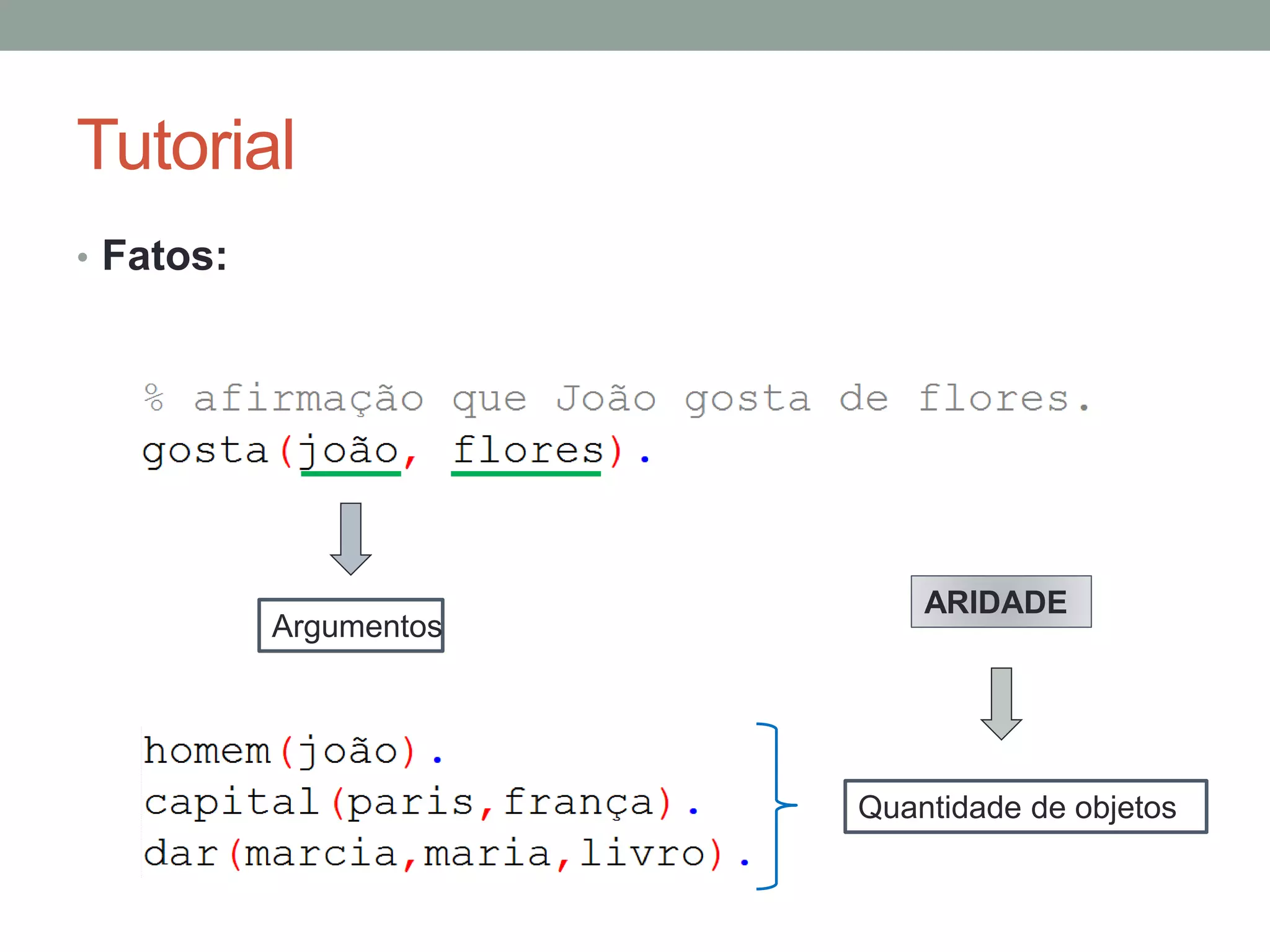
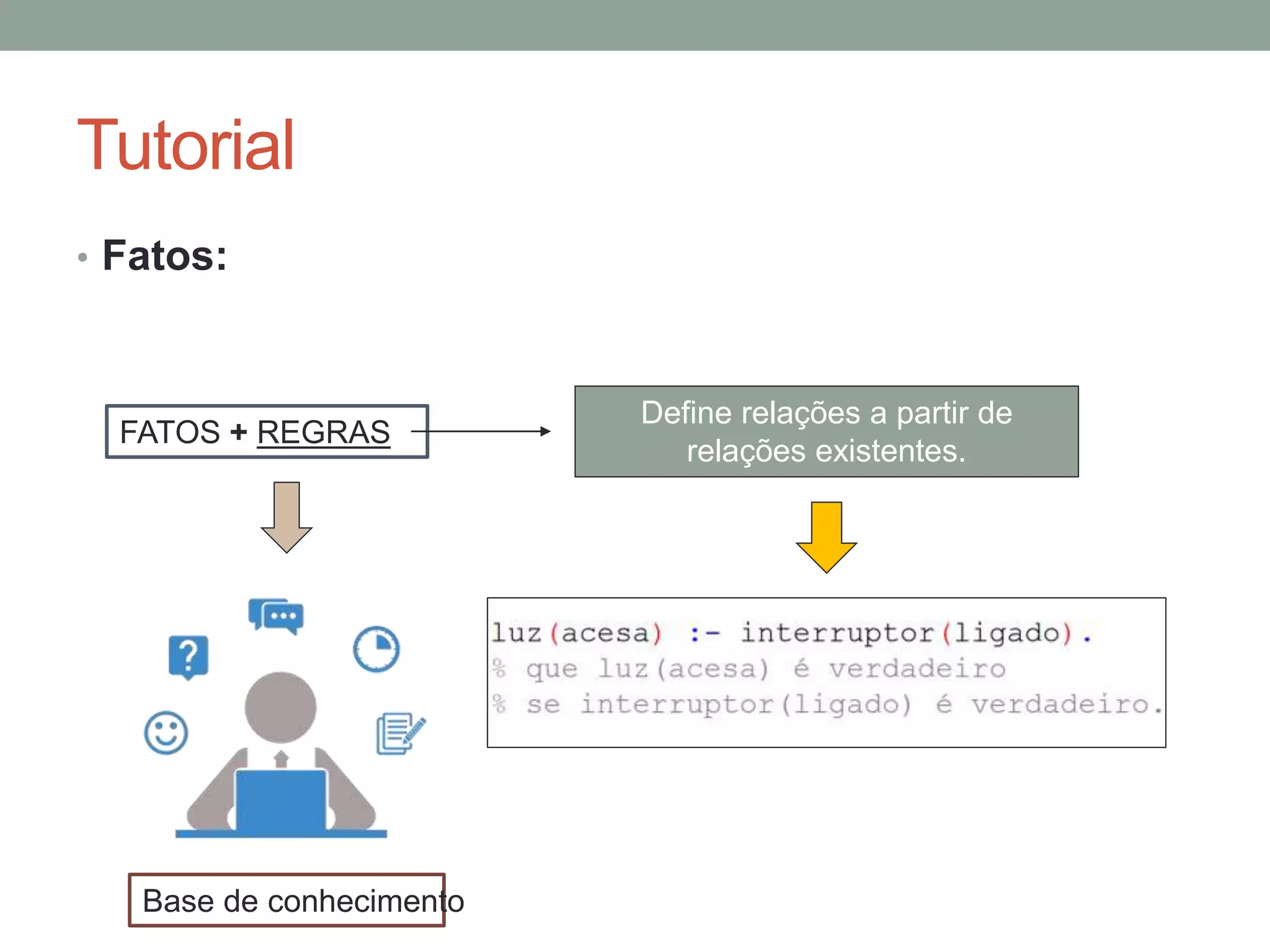
Prolog é uma linguagem de programação lógica baseada nos princípios da lógica declarativa. O documento introduz os principais conceitos de Prolog, incluindo: 1) Fatos representam afirmações sobre objetos do domínio. 2) Regras definem novas relações em termos de outras relações. 3) Consultas verificam se uma afirmação é verdadeira baseado nos fatos e regras.

1. INTRODUÇÃO AO
PROLOG
Prof. Sérgio Souza Costa

2. Roteiro
1. Introdução
2. Princípios
3. Tutorial

3. Introdução
• Um pequeno artigo fácil de ler e destaco os elementos
apresentados nesse seminário:
• http://www.ime.usp.br/~slago/IA-Prolog.pdf

4. Introdução
• Prolog:
• Linguagem declarativa baseado nos princípios da lógica;
• Utilizada na Inteligência Artificial;
• Focada na especificação do conhecimento;
• Desenvolvida em 1972 por Alain Colmerauer e Philippe Roussel.
ALAIN COLMERAUER
Computer scientist
About
Link: http://alain.colmerauer.free.fr/
The birth of Prolog
Link: Clique aqui.
Aspects of PROLOG History:
Logic Programming and Professional Dynamics
Link: Clique aqui.

5. Introdução
• Online: http://swish.swi-prolog.org
• Instalação:
• SWI-Prolog:
• É uma IDE para desenvolvimento (Free).
• Download:
• Link: http://www.swi-prolog.org/

6. Introdução
• Histórico:
• Ideia:
• Desenvolver uma linguagem de programação baseada em lógica.
• Início de aplicações industriais (1981);
• O primeiro compilador (1982);
• Em 1992, a definição de normas ISO para Prolog.

7. Introdução
• Aplicações:
• Tratamento de linguagem natural;
• Banco de dados;
• Automação de projetos;
• Sistemas especialistas;
• Entre outros.

8. Princípios
• Características:
• Especificação da solução em termos de relações entre entidades;
• Descreve o universo do problema;
• Lógica matemática;
• Um conjunto de afirmações.
NÃO é uma descrição da solução do problema
Problema
Um conjunto de perguntas sobre os
objetos do universo da aplicação

9. Princípios
Prolog é baseada em um subconjunto da linguagem do cálculo de
predicados, linguagem das cláusulas de Horn.

10. Princípios
• Sujeito apreende no intelecto o conceito de objeto (ex:
casa, branca).
• Os conceitos são ligados, e formam juízos (ex: a casa é
branca).
• Os conceitos são externalizados como termos, e os juizos
como proposições.

11. Princípios
• Sujeito apreende no intelecto o conceito de objeto (ex:
casa, branca).
• Os conceitos são ligados, e formam juízos (ex: a casa é
branca).
• Os conceitos são externalizados como termos, e os juizos
como proposições.
• Mas qual a estrutura geral da proposição ?

12. Princípios
• Estrutura geral da proposição, segundo Aristóteles:
A casa é branca.
Quantificador: Alguma
termo/sujeito: Casa
Cópula: é
termo/predicado: Branca

13. Princípios
• Estrutura geral da proposição, segundo Frege:
• Uma proposição é estrutura abstrata composta por função e
argumento (nota: conceito matemático)
• Deslocou a atenção da distinção sujeito-predicado para a distinção
função-argumento.

14. Princípios
• Uma função em matemática é uma generalização de uma
expressão, ou seja, é uma expressão que contêm um
espaço vazio.
• ... + 2
• A ... é branca
• A casa e …
• ... gosta …

15. Princípios
• Uma função em matemática é uma generalização de uma
expressão, ou seja, é uma expressão que contêm um
espaço vazio.
• ... + 2, X + 2
• A ... é branca, X é branca
• A casa e …, A casa é X
• ... gosta …, X gosta de Y

16. Princípios
• Uma função em matemática é uma generalização de uma
expressão, ou seja, é uma expressão que contêm um
espaço vazio.
• ... + 2, X + 2, f(x) = x + 2
• A ... é branca, X é branca, branca(X)
• A casa e …, A casa é X, casa(X).
• ... gosta …, X gosta de Y, gosta(X,Y)

17. Princípios
• Exemplo de implicações:
• Todos os homens são mortais.
• Todo A tem a propriedade B
• Qualquer que seja X, se X tem a propriedade A, então X tem a
propriedade B.
• Ou, ∨x (Ax -> Bx )

18. Introdução
• O motivo disso é simplesmente destacar a conclusão da
implicação.
• q é a cabeça e p é o corpo da implicação
• Em Prolog escrevemos uma implicação do tipo
q ← p, é escrita como q :- p.
• Todo programa em Prolog é só isso 
Em cláusula Horn, podemos escrever uma implicação
do tipo p → q de maneira inversa, ou seja,
q ← p.

19. Assertion and Clause
• A simple assertion has the form r(T1, . . . , Tm) where r is
an m-ary relation, and where T1, . . . , Tm are terms
(expressions), possibly containing variables.
• A clause (or just clause) has the form:
A0 if A1 and ... and An.
• Informally, this clause means that, if the assertions A1 , . .
. , An are all true, then we can infer that the assertion A0
is also true.
• A fact is a special case of a Horn clause where n = 0:
A0.
PROGRAMMING LANGUAGE. DESIGN CONCEPTS. David A. Watt,

20. Assertion and Clause
• A PROLOG clause is a Horn clause written in one of the
following forms:
A0.
A0 :- A1, ..., An.
• The first of these is a fact. The second is read as ‘‘A0
succeeds if A1 succeeds and . . . and An succeeds’’.
PROGRAMMING LANGUAGE. DESIGN CONCEPTS. David A. Watt,

21. Assertion and Clause
• A PROLOG clause may also contain the symbol ‘‘;’’, which
means ‘‘or’’. For example:
A0 :- A1; A2, A3.
• is read as ‘‘A0 succeeds if either A1 succeeds or A2
succeeds and A3 succeeds’’. This is just an abbreviation
for a pair of Horn clauses, ‘‘A0 :- A1.’’ and ‘‘A0 :- A2, A3.’’.
PROGRAMMING LANGUAGE. DESIGN CONCEPTS. David A. Watt,

22. Assertion and Clause
irmao(X,Y) :- filho(X, H,M) , filho(Y,H,M) , Y == X.
Cabeça, da
clausula
Pescoço,
equivale ao “if“
ou “se”.
Corpo da
clausula.
Uma virgula (,) equivale ao
operador “e” e um ponto e
virgula (;) ao operador “ou”.
Pé da
clausula(.)

23. Assertion and Clause
irmao(X,Y) :- filho(X, H,M) , filho(Y,H,M) , Y == X.
Cabeça, da
clausula
Pescoço,
equivale ao “if“
ou “se”.
Corpo da
clausula.
Uma virgula (,) equivale ao
operador “e” e um ponto e
virgula (;) ao operador “ou”.
Pé da
clausula(.)
ama(joao,maria).
Cabeça, da
clausula
Regras são clausulas com
corpo, e fatos são cláusulas
sem corpo.

24. Query
• Computation consists of testing a given query Q, which in
its simplest form is just an assertion. If we can infer from
the clauses of the program that Q is true, then we say that
the query succeeds. If we cannot infer that Q is true, then
we say that the query fails.

25. Resumo
• Fatos:
• Afirmações corretas sobre os objetos do universo da aplicação
(verdades incondicionais).
• Exemplo: A prova de lógica é fácil.
• Regras:
• Cláusulas com condicionais.
• Exemplo: A prova de lógica é fácil se a turma estudar.
• Consultas:
• Verificação de uma verdade.
• A prova de logica é fácil ?
• Qual prova é fácil?

26. Tutorial
• Acessem:
• http://swish.swi-prolog.org

27. Tutorial
• Fatos:
• Cada fato exprime um relacionamento entre os objetos envolvidos.
• Exemplos:
Predicados

28. Tutorial
• Fatos:
Argumentos
ARIDADE
Quantidade de objetos

29. Tutorial
• Fatos:
Em um mesmo programa podemos ter um mesmo predicado com
aridades diferentes.
EXEMPLOS

30. Tutorial
• Fatos:
FATOS + REGRAS
Base de conhecimento
Define relações a partir de
relações existentes.

31. Tutorial
• Consultas:
• É uma pergunta sobre os fatos da base de dados.
• Em Prolog, a pergunta é similar sintaticamente aos fatos.
• Exemplos:
Informativo
Algumas vezes será
possível encontrar:
:-
ao invés de:
?-

32. Tutorial
• Consultas:
• Realiza um pattern matching entre a pergunta e os fatos (base de
dados).
Objetivo - Prolog
V F
O F (false) deve
ser entendido
como:
Não é provável.

33. Tutorial
• Princípios da programação:
• Consultas:
• Como responder: “Quem gosta de flores?”.
• Uso de variáveis.
• Exemplo:
Procura (na base) todas as instâncias possíveis (os objetos) de X (True).
Letra maiúscula.

34. Tutorial
• Consultas:
• Exemplos:

35. Tutorial
• Consultas:
• Conjunção: combina objetivos na mesma pergunta.
• É preciso separar os objetivos por uma vírgula (,).
• Exemplos:
Quem são os ‘Maranhenses’ que gostam de ‘flores’?
(Tenta satisfazer todos os objetivos, em ordem).

36. Tutorial
• Regras:
• É uma generalização das afirmações sobre os objetos do universo
da aplicação.
• Permitem definir novas relações em termos de outras relações já
existentes.
• Exemplo com conjunção:
Estabelece que X é avô de Y se X tem um filho Z que é pai
de Y.

37. Tutorial
• Regras:
• Exemplo - Grafo de relacionamento:

38. Tutorial
• Regras:
• Exemplo - Grafo de relacionamento (irmão):

39. Tutorial
• Regras:
• Exemplo - (irmão):

40. Tutorial
• Regras:
• Exemplo com disjunção:
A disjunção pode ser expressa, dividindo-se a regra:

41. Todas as familias:
Atividade (game of thrones):
Escrever as regras no link
abaixo:
http://swish.swi-
prolog.org/p/WKPvOLZI.pl