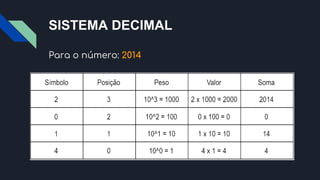
O documento aborda sistemas numéricos, explicando conceitos básicos como símbolos, valores e posições em diferentes sistemas (decimal, binário e hexadecimal). Ele destaca a importância de compreender como os números são representados e a função de cada sistema em computação e matemática. Ao final, sugere que os leitores compartilhem o conhecimento adquirido com outros.

1. SISTEMAS
NUMÉRICOS

2. SOBRE O CONTEÚDO
O conteúdo a seguir é de interesse para cursos como Análise e
Desenvolvimento de Sistemas, Ciência da Computação, Engenharia
da Computação e Matemática Pura. O objetivo do material é fazê-lo
entender como se define os valores de um número usando os
símbolos e o peso das posições determinadas para cada sistema de
numeração. O nível da abordagem do assunto é básico! No final
desse estudo, compartilhe essa fonte com outras pessoas para
ajudar na democratização do conhecimento.
Guilherme Donizetti - guilhermedonizettiads@gmail.com

3. O que é SISTEMA NUMÉRICO?
É um conjunto de símbolos e valores para a
representação de um número.
EXEMPLO: “Século XXI” tem o mesmo significado de
“Século 21”.
O exemplo acima mostra dois sistemas, onde
ambos representam com símbolos diferentes o
mesmo número “vinte e um”.

4. E SISTEMA NUMÉRICO POSICIONAL?
Também é um conjunto de símbolos e valores para
representação de um número, mas o valor será
definido pela posição em que se encontra o
símbolo.
EXEMPLO: em “27” o 2 vale vinte. em “72” o 2 vale dois.
O exemplo acima mostra que o mesmo símbolo
recebe valor diferente variando sua posição.

5. QUE FIQUE CLARO!!!
Símbolo: a representação para um número,
portanto os algarismos são símbolos. “4” é um
símbolo, assim como IV também é.
Valor: quantidade de vezes que o peso da posição
aconteceu.
Posição: na representação de um número, onde se
encontra cada símbolo. “23”, 3 está na primeira
posição e 2 está na segunda.

6. DECIMAL (BASE 10)
BINÁRIO (BASE 2)
HEXADECIMAL (BASE 16)

7. SISTEMA DECIMAL
O mais comum, por ser utilizado em nosso dia-a-
dia, é o que podemos também chamar de base 10.
Símbolos: 0 1 2 3 4 5 6 7 8 9
Para representar um valor, é necessário usar um
ou alguns dos símbolos acima.

8. SISTEMA DECIMAL
Em decimal, o valor é de acordo com a posição. Se
alguém disser que leu 58 páginas de um livro, está
querendo dizer que leu 50 + 8 páginas, contudo,
por que não representar isso com “508”?
AS POSIÇÕES…
Em 58, “8” é a primeira posição e “5” é a segunda!

9. SISTEMA DECIMAL
Cada posição possui um peso (medida de um valor).
Esse peso será definido por uma potência de 10 e o
expoente será a ordem da posição. A posição inicial
é 0 e sua continuidade é da direita para a
esquerda.

10. DEMONSTRAÇÃO DE VALOR EM
DECIMAL
O valor de um número é a somatória da
multiplicação do símbolo pelo peso.
Veja o exemplo a seguir...

11. SISTEMA DECIMAL
Para o número: 2014

12. SISTEMA BINÁRIO
Sistema básico para os computadores, também
chamado de base 2.
Símbolos: 0 1
Para representar um valor na base 2, usa-se
apenas esses dois símbolos em formato de octeto,
isto é, em oito posições, ex.: 10010111

13. SISTEMA BINÁRIO
O peso da posição em binário é definido por uma
potência de 2 e o expoente é a ordem da posição.

14. SISTEMA BINÁRIO
Para visualizar um número em binário é diferente: o
peso da posição onde o símbolo for 0 será
ignorado, e onde o símbolo for 1 será somado.
Podemos definir como:

15. SISTEMA BINÁRIO
Portanto, dado o número 00010011

16. SISTEMA BINÁRIO
A somatória de todos os valores não ignorados, ou
seja, valor da posição onde o símbolo é 1, será igual
a 19.
Assim, dizemos que 00010011 e 19 são os mesmos
números representados por símbolos diferentes,
ambos têm o mesmo valor: dezenove.

17. SISTEMA HEXADECIMAL
Muito utilizado para a compactação de números
binários, também chamado de base 16.
Símbolos: 0 1 2 3 4 5 6 7 8 9 A B C D E F
Para representar um valor na base 16 faz-se uso
desses símbolos, no formato de dupla, isto é, dois
elementos, ex.: D7

18. SISTEMA HEXADECIMAL
Por que hexadecimal serve para compactar o
formato binário? Cada elemento representa a
metade de um octeto binário:
hexadecimal: D7
octeto: 11010111
metades: D representa (1101), 7 representa (0111)

19. SISTEMA HEXADECIMAL
Problema:
Dado um número na base 2, como representá-lo na
base 16?
1. dividir octeto em duas partes (se não existir 8
posições, complete com 0 à esquerda);
2. conhecer o valor decimal de cada parte;

20. SISTEMA HEXADECIMAL
3. confira na tabela de relações como representar
em hexadecimal os dois números obtidos no passo
anterior.
HEX 0 1 2 3 4 5 6 7 8 9 A B C D E F
DEC 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

21. SISTEMA HEXADECIMAL
1) Exercício explicado:
Tínhamos o número 115 e o convertemos para
binário, ficando 1110011. Como deixar esse número
menor usando base 16?
Note que o binário não é um octeto, portanto não
possui oito posições ocupadas. Resolução...

22. SISTEMA HEXADECIMAL
1. Divida o octeto, nesse caso acrescente 0 à
esquerda: 01110011. SEPARADOS: (0111) e (0011);
2. Valor decimal das partes. Usando o
conhecimento sobre SISTEMA BINÁRIO,
descobrimos que: 0111 vale 7 e 0011 vale 3;
3. Consultando a tabela de relações vemos que 7
em Hex é representado por 7 e 3 representado
por 3.
115 (dec) = 01110011 (bin) = 73 (hex)

23. SISTEMA HEXADECIMAL
2) Exercício explicado:
Simplifique o binário 10100111 usando base 16.
Resolução...

24. SISTEMA HEXADECIMAL
1. Divida o octeto. SEPARADOS: (1010) e (0111);
2. Valor decimal das partes. Usando o
conhecimento sobre SISTEMA BINÁRIO,
descobrimos que: 1010 vale 10 e 0111 vale 7;
3. Consultando a tabela de relações vemos que 10
em Hex é representado por A e 7 representado
por 7.
144 (dec) = 10100111 (bin) = A7 (hex)

25. PRATIQUE!
Dado o número 10010010:
Sua representação decimal =
Sua representação hexadecimal =
Dado o número 1010010:
Sua representação decimal =
Sua representação hexadecimal =

26. Observa-se que esse conteúdo não ensinou
conversão de bases numéricas, porquanto o objetivo
é fazer entender o que é um sistema numérico com
algumas práticas para que o próximo passo não seja
automático, mas compreendido.
➢ Se você entendeu esse conteúdo, avance para o estudo
de conversões de bases numéricas.

27. GUILHERME DONIZETTI
Acadêmico em Análise e Desenvolvimento de Sistemas - Faculdade de
Tecnologia do Estado de São Paulo, Cruzeiro - São Paulo.
Técnico em Informática - Escola Técnica Estadual de São Paulo 077 -
Cruzeiro - São Paulo
Conteúdo (Web): Sistemas Numéricos
Disponível: guilhermedonizettiads@gmail.com
Data: Abril, 2020.