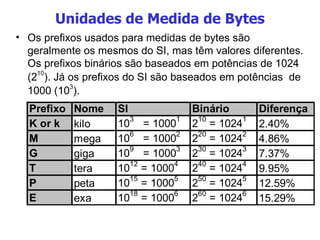
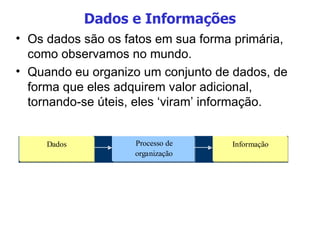
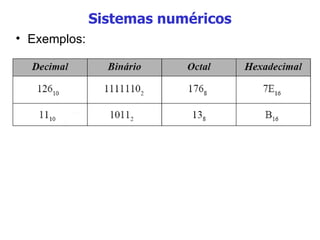
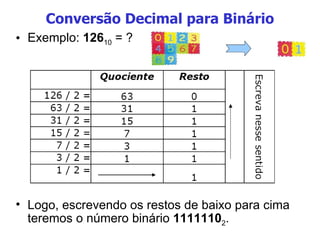
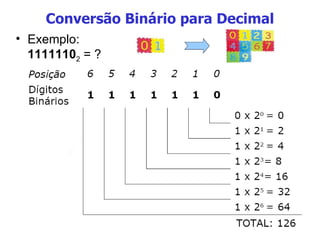
O documento discute sistemas numéricos, unidades de medida de bytes e a diferença entre dados e informações. Em particular, explica que (1) sistemas numéricos como binário, octal e hexadecimal são usados em computação, (2) bytes são conjuntos de 8 bits usados para medir armazenamento digital, e (3) dados se tornam informação quando organizados de forma significativa.

1. Bits, Bytes, Sistemas Numéricos e Conversões Regis Pires Magalhães [email_address] Última atualização em 20/04/2007

2. Sistema binário A ciência da computação não foi a primeira a usar o sistema binário. Os papuas, habitantes da Nova Guiné, são uma tribo tão primitiva que até hoje ainda não aprenderam a contar com os dedos. Há milênios, eles se utilizam de um rudimentar sistema binário. Há um símbolo para 1, outro para 2, e daí em diante, para qualquer quantidade, emprega-se um grunhido que significa imensamente mais .

3. Sistemas numéricos Estamos acostumados à prevalência métrica de base 10, mas muitas matemáticas foram construídas tendo como base o 60 - uma herança que recebemos os babilônios, há 40 séculos - e não o 10. O triunfo do 10, fruto da prosaica vitória de nossas mãos e pés de dez dedos, não impediu, no entanto, que a base 60 ainda seja amplamente usada - no contar das horas e dos graus, por exemplo - e que conviva com o atual reinado da base decimal.

4. Bit Abreviação de dígito binário ( bi nary digi t ). Unidade básica de armazenamento de informação. Embora os computadores tenham instruções para manipulação de bits, geralmente são idealizados para armazenar instruções em múltiplos de bits, chamados bytes.

5. Bytes Conjunto de 8 bits. O byte de 8 bits é, por vezes, também chamado de octeto . Originalmente o byte tinha tamanho variável. A metade de um byte, dá-se o nome de nibble ou semioctecto. Exprimem-se as quantidades de bytes em prefixo binário (e não no Sistema Internacional de Unidades). Têm o mesmo nome das unidades do SI, embora sejam múltiplos de 1024 (2 10 ) no lugar de 1000 (10 3 ).

6. Unidades de Medida de Bytes Os prefixos usados para medidas de bytes são geralmente os mesmos do SI, mas têm valores diferentes. Os prefixos binários são baseados em potências de 1024 (2 10 ). Já os prefixos do SI são baseados em potências de 1000 (10 3 ).

7. Medições Na transmissão de dados entre computadores, geralmente usa-se medições relacionadas a bits e não a bytes. Ex: 300 Kb (Kilobits) Quando a medição é feita em bytes, o B da sigla é maiúsculo (como em GB). Quando a medição é feita em bits, o b da sigla fica em minúsculo (como em Gb).

8. Dados e Informações Os dados são os fatos em sua forma primária, como observamos no mundo. Quando eu organizo um conjunto de dados, de forma que eles adquirem valor adicional, tornando-se úteis, eles ‘viram’ informação.

9. Dado e Informação Dado – fenômeno qualquer sem significado . Dados podem ser armazenados em um computador e processados por ele . No momento em que o dado é contextualizado passa a ser identificado como uma informação . Informação – dado com significado . Abstração informal (não pode ser formalizada através de uma teoria lógica ou matemática), que está na mente de alguém , representando algo significativo para essa pessoa. O que é armazenado na máquina não é a informação, mas a sua representação em forma de dados. Assim, não é possível processar informação diretamente em um computador. Computadores não possuem qualquer entendimento. Eles não podem pensar porque lhes falta a nossa semântica.

10. Sistemas numéricos Mais comuns: Decimal (base 10) É a usada normalmente Os dígitos válidos vão de 0 a 9 Exemplo: 126 10 (normalmente escreve-se somente 126) Binário (base 2) Os dígitos válidos são 0 e 1 Exemplo: 1111110 2 Octal (base 8) Os dígitos válidos vão de 0 a 7 Exemplo: 176 8 Hexadecimal (base 16) Os dígitos válidos vão de 0 a 9 e de A até F (ou do a até f) Exemplo: 7E 16

11. Sistemas numéricos Exemplos:

12. Conversão Decimal para Binário Dividir por 2 e obter o resto (que é ou 0 ou 1) Este dígito fará parte da forma binária do número a encontrar Obter o quociente e divida novamente por 2 Repetir o processo até que o quociente alcance 0 ou 1 Os restos do início ao fim representam o resultado em forma binária NOTA: O último dígito menor que o divisor (2) será o primeiro número do resultado

13. Conversão Decimal para Binário Exemplo: 126 10 = ? Logo, escrevendo os restos de baixo para cima teremos o número binário 1111110 2 .

14. Conversão Binário para Decimal Multiplicar os dígitos binários pela “potência de 2 na posição do número binário”. Somar todos os produtos para obter como resultado o número decimal.

15. Conversão Binário para Decimal Exemplo: 1111110 2 = ?

16. Referências Revista Odisséia Digital http://pt.wikipedia.org http://en.wikipedia.org Dado, Informação, Conhecimento e Competência - Valdemar W. Setzer http://www.ime.usp.br/~vwsetzer/dado-info.html Projeto JEDI – Introdução à Programação I – Slides Lição 1 – Introdução à programação de computadores.