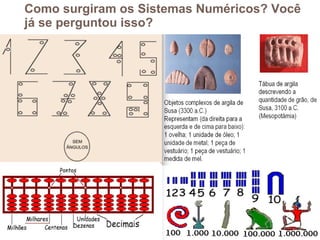
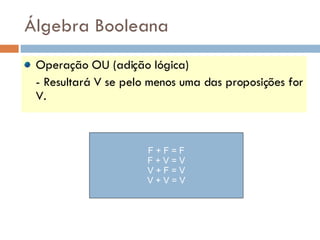
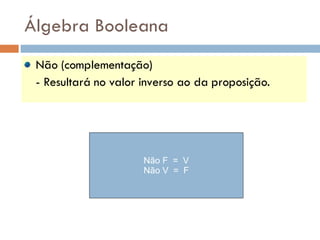
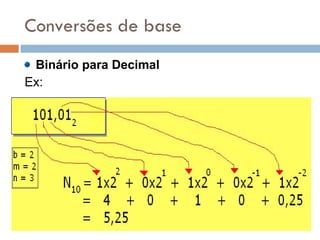
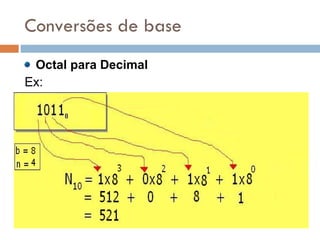
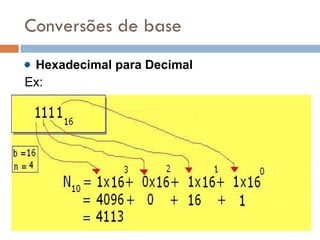
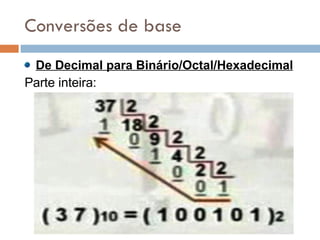
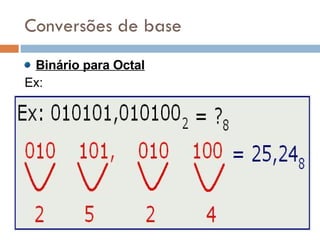
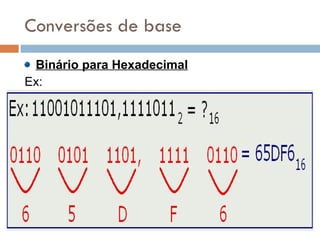
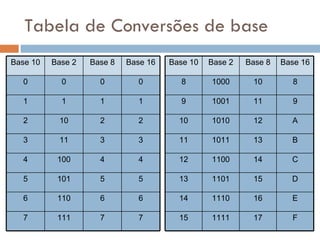
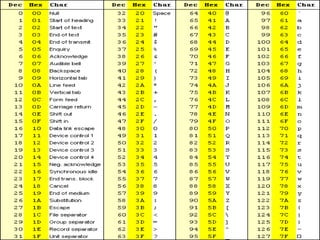
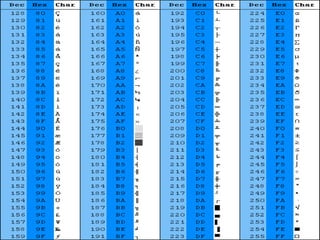
1) O documento discute sistemas de numeração, incluindo o binário, e como eles são usados para representar informações nos computadores. 2) Sistemas posicionais como o decimal, octal e hexadecimal são explicados, assim como conversões entre bases. 3) O sistema binário é particularmente importante porque é a base usada pelos computadores para representar dados.

1. Componentes do grupo Alexis Anne Carolline Plínio Eduardo Tâmara Taxman Victor Vinícius Apresentação

2. Representação da Informação Mas, afinal, o que é INFORMAÇÃO? Na verdade, toda e qualquer grandeza do mundo real, desde as cores e posições dos pontos que formam a imagem de Monalisa, os compassos, timbres e notas musicais que compõem a Quinta Sinfonia de Beethoven, o conjunto de caracteres que consubstanciam a Divina Comédia até a sucessão ordenada de aminoácidos que formam o DNA dos seres vivos. Em suma: toda e qualquer criação humana ou da natureza, seja ela qual for, pode ser codificada e representada (com maior ou menor precisão) sob forma de um conjunto de números. E estes números podem ser expressos no sistema binário.

3. Como surgiram os Sistemas Numéricos? Você já se perguntou isso?

4. Conceitos Iniciais de Sistemas de Numeração Objetivos P rover símbolos e convenções para representar quantidades, de forma a registrar a informação quantitativa e poder processá-la. A representação de quantidades se faz com os números . Sistema de Numeração Romano Como utiliza símbolos (letras), seria bastante complicado realizar operações. Experimente multiplicar CXXVIII por XCIV ! Posteriormente foram criados outros sistemas que resolveriam esse problema.

5. Sistemas de Numeração Posicionais Conceito Um exemplo de Sistema Posicional é o que usamos no nosso dia-a-dia, o Sistema Decimal. 125 = 1x102 + 2x101 + 5x100

6. Tipos de Sistemas Posicionais Sistema Decimal Possui base 10, utilizando os símbolos: 0,1,2,3,4,5,6,7,8,9. Sistema Octal Possui base 8, utilizando os símbolos: 0,1,2,3,4,5,6,7. Sistema Hexadecimal Possui base 16, utilizando os algarismos 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Sistema Binário Possui base 2, utilizando os algarismos 0,1.

7. Fórmula para Cálculo do valor Posicional V - Valor posicional do símbolo . S - Valor absoluto do símbolo. B - Base do sistema numérico. É a quantidade de símbolos que dispomos para escrever os números. P - É a posição em que o símbolo em questão se encontra no número. Esta posição é definida da direita para esquerda e inicia em zero. V = S * B ^ P

8. Facilita a representação dos estados da corrente elétrica Ligado/Desligado Por que utilizar o Sistema Binário? Ligado = 1 Desligado = 0

9. Álgebra Booleana Busca pela transposição do domínio verbal ao domínio matemático. domínio verbal  ambíguo X domínio matemático  preciso

10. Álgebra Booleana Em 1854, George Boole publica o ensaio ‘Uma Investigação das Leis do Pensamento’; Concepção de uma espécie de álgebra, Um sistema de símbolos e regras aplicável a qualquer coisa, desde números e letras, a objetos ou enunciados

11. Álgebra Booleana Através dessa álgebra, Boole pode codificar proposições em linguagem simbólica, e então manipulá-las quase da mesma maneira como se faz com os números ordinais. Ex: o Sol é verde < a Terra é um planeta 0 < 1

12. Álgebra Booleana Operações Básicas: OU E Não

13. Álgebra Booleana Operação OU (adição lógica) - Resultará V se pelo menos uma das proposições for V. F + F = F F + V = V V + F = V V + V = V

14. Álgebra Booleana Operação E (multiplicação lógica) - Resultará V apenas se todas as proposições forem V. F . F = F F . V = F V . F = F V . V = V

15. Álgebra Booleana Não (complementação) - Resultará no valor inverso ao da proposição. Não F = V Não V = F

16. Teorema Fundamental da Numeração Onde: N – número equivalente na base 10 d – dígito para conversão b – base do sistema ao qual será convertido i – índice do dígito ou expoente da base m – quantidade de dígitos à direita da vírgula n – quantidade de dígitos à esquerda da vírgula

17. Conversões de base Binário para Decimal Ex:

18. Conversões de base Octal para Decimal Ex:

19. Conversões de base Hexadecimal para Decimal Ex:

20. Conversões de base De Decimal para Binário/Octal/Hexadecimal Parte inteira:

21. Conversões de base De Decimal para Binário/Octal/Hexadecimal Parte fracionária

22. Conversões de base Binário para Octal Ex:

23. Conversões de base Binário para Hexadecimal Ex:

24. Tabela de Conversões de base 7 7 111 7 6 6 110 6 5 5 101 5 4 4 100 4 3 3 11 3 2 2 10 2 1 1 1 1 0 0 0 0 Base 16 Base 8 Base 2 Base 10 F 17 1111 15 E 16 1110 14 D 15 1101 13 C 14 1100 12 B 13 1011 11 A 12 1010 10 9 11 1001 9 8 10 1000 8 Base 16 Base 8 Base 2 Base 10

25. Tabelas de Representação Quais as formas para se representar a informação? Os computadores manipulam dados de sinais brutos para produzir informações. Os dados são convertidos em informações e estes em dados novamente. Assim são produzidas as informações. Uni código. UNICODE Código padrão americano para o intercâmbio de informações. ASCII Código ampliado de caracteres decimais codificados em binários para o intercâmbio de dados. EBCDIC Números decimais codificados em binários. BCD

26. Tabela ASCII ASCII (para American Standard Code for Information Interchange , que em português significa &quot; Código Padrão Americano para o Intercâmbio de Informação &quot;) . É um conjunto de códigos para o computador representar números, letras, pontuação e outros caracteres. Surgido em 1961, um dos seus inventores foi Robert W. Bemer. ASCII é uma padronização da indústria de computadores, onde cada carácter é manipulado na memória sob forma de código binário. O código ASCII é formado por todas as combinações possíveis de 8 bits.

29. Complemento de dois É o sistema mais usado para representação de números inteiros com sinal nos computadores modernos. O dígito mais significativo, à esquerda do número, é o que informa seu sinal. Se este dígito for zero (0) o número é positivo e se for um (1) é negativo . Pela definição, só existe uma representação para o zero e ela é 0000...0 Para obtermos o complemento de 2 de um número binário, precisamos inicialmente converter o número em seu complemento de 1,que obtém-se trocando cada bit pelo seu complemento (0  1 e 1  0). A seguir, soma-se 1 ao complemento de 1, obtendo assim o complemento de 2

30. Complemento de dois Vamos exemplificar obtendo os complementos de 2 dos números binários abaixo: binário compl de 1 compl de 2 10001001 01110110 01110111 00111100 11000011 11000100 Devemos observar que devido ao seu emprego em hardware os números binários são representados sempre com um número fixo de bits. A conversão inversa, ou seja, de um número em representação complemento de 2 para a notação binária original é feita obtendo-se novamente o seu complemento de 2.

31. Adição Binária A adição no sistema binário é realizada exatamente da mesma forma que uma adição no sistema decimal. Vamos verificar quais os possíveis casos que ocorrerão na soma por colunas: a)0 b)0 c)1 d)1 e)1 +0 +1 +0 +1 1 ---- ---- ---- ----- +1 0 1 1 10 ----- 11 Exemplo: 1101+1011, temos: 11000.

32. Subtração Binária Como o método também é análogo ao da subtração no sistema decimal, vamos ver quais os possíveis casos que ocorrerão na subtração por colunas. a) 0 b) 0 c)1 d)1 -0 -1 -0 -1 ---- ---- ---- ---- 0 1 1 0 Exemplo: 1110 – 1001, temos: 0101.

33. Multiplicação Binária Também análoga ao caso decimal. Agora os casos possíveis são: a) 0x0 = 0 b) 0x1 = 0 c) 1x0 = 0 d) 1x1 = 1 Exemplificando, efetuar 11110 x 11: 11110 x 11 ------------- 11110 11110 + ------------- 1011010