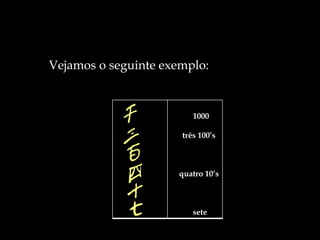
O documento descreve a evolução histórica dos sistemas de numeração ao longo dos séculos, desde as marcas feitas em pedras e ossos pelos povos antigos até o sistema de numeração arábico utilizado atualmente. Detalha os sistemas de numeração egípcio, babilônico, chinês-japonês, romano e maia, destacando suas particularidades. Explica também como o sistema de numeração indo-arábico, com seu caráter decimal e uso do zero, tornou-se o mais prático e se

1. Um pouco de História

2. Curso: Novas Tecnologias no Emnsino da
Matemática.
Disciplina: Informática Eucativa II (2010).
Aluna: Renata de Assumção Monteiro
Domingos.
Polo: Iguaba Grande

3. Desde a antiguidade, muitos povos utilizaram
diferentes formas de registrar contagens: marcas
ou riscos feitos em paredes, ossos ou madeira.
Uma dificuldade que as pessoas provavelmente
encontravam, há milhares de anos, era trabalhar
com grandes quantidades. Afinal, registrar essas
quantidades empilhando pedras ou fazendo
marcas na madeira era difícil e pouco prático.
Então, veio a idéia de agrupar, para visualizar
melhor as quantidades, criando símbolos especiais
para esses agrupamentos e regras para registrar
quantidades com esses símbolos. Surgiam, então,
os primeiros sistemas de numeração que serão
nosso objeto de estudo neste trabalho.

4. Os antigos egípcio contavam formando grupos
de dez. Neste sistema, um mesmo símbolo só podia ser
repetido nove vezes. Cada agrupamento de dez era
trocado por um novo símbolo. Vejamos a tabela a
seguir:

5. Vejamos alguns exemplos:
Para representar 332, os egípcios escreviam:
|| , ou seja, 100+100+100+10+10+10+1+1.
Para representar 4569, os egípcios escreviam:
|||||||||, ou seja,
1000+1000+1000+1000+100+100+100+100+100+10+10+
+10+10+10+10+1+1+1+1+1+1+1+1+1.
No entanto, este sistema de numeração pode
tornar-se muito trabalhoso em relação à
representação dos números.

6. As matemáticas mesopotâmicas atingiram
um nível mais elevado do que o obtido pelas
matemáticas egípcias. Na Mesopotâmia
podemos mesmo detectar um certo progresso
no decorrer dos séculos. Os textos mais antigos,
datados do terceiro milênio do último período
sumério, revelam já uma grande habilidade
para calcular. Estes textos contêm tábuas de
multiplicação nas quais um sistema
sexagesimal se sobrepõe a um sistema decimal.

7. Enquanto os egípcios indicavam cada
unidade mais elevada através de um novo
símbolo, os Babilônicos usavam o mesmo
símbolo, mas indicavam o seu valor pela sua
posição. Assim, 1 seguido por outro 1
significava 61 e 5 seguido por 6 e por 3 (5,06,03)
significava 5x602+6x60+3=18.363. Este sistema
de posição não diferia essencialmente do nosso
próprio sistema de escrita de números, em que
o símbolo 343 representa 3x102+4x10+3. Tal
sistema tinha vantagens enormes para o
cálculo.

8. Entre os sistemas de numeração mais
antigos encontram-se o utilizado pelos chineses
e adotado mais tarde pelos japoneses.
O sistema de numeração Chinês-Japonês
difere do sistema de numeração grego porque
utiliza múltiplos de 10, 100 e 1000.
Uma curiosidade deste sistema de
numeração é que ele utiliza uma escrita
vertical.

9. Vejamos o seguinte quadro que ilustra a
representação de cada número no sistema
Chinês-Japonês:

10. Vejamos o seguinte exemplo:
1000
três 100’s
quatro 10’s
sete

11. Os antigos romanos possuíam um sistema
de numeração formado por sete símbolos.
Símbolos Valores
I 1
V 5
X 10
L 50
C 100
D 500
M 1000

12. Repetindo cada símbolo duas ou três vezes
(nunca mais que três) o número fica duas ou três
vezes maior: Os símbolos V, L e D não se repetem.
As letras I, X ou C colocam-se à esquerda de
outras de maior valor para representar a diferença
deles, obedecendo às seguintes regras:
 I só se coloca à esquerda de V ou de X;
 X só se coloca à esquerda de L ou de C;
 C só se coloca à esquerda de D ou de M.
Se a um símbolo colocarmos à sua direita um
símbolo de menor valor, este último símbolo soma o
seu valor ao valor do outro.
Vejamos um quadro com exemplos desses
números

14. Durante mais de 1000 anos, o sistema de
numeração romano foi utilizado na Europa. Por
volta do século XIII, com a expansão do comércio e
das navegações, os símbolos romanos foram
substituídos pelos algarismos indo-arábicos.
Hoje a numeração romana ainda é utilizada em
algumas situações, como nos mostradores de
alguns relógios, na escrita dos números dos
séculos, na numeração de capítulos de livros e de
leis, na designação de reis e papas de mesmo nome
etc.

15. Os Maias tinham como base não a dezena,
mas a vintena e as potências de vinte. A razão,
como se sabe, é devida ao hábito que os seus
ancestrais tinham de contar não apenas com os
dez dedos, mas também com os seus pés.
A numeração do povo Maia fundou-se no
princípio da adição. Devia associar um círculo
ou um ponto à unidade (sinal comum a todos
os povos da América Central, originado do
grão de cacau, então empregado como "moeda
de troca").

17. Como vimos, muitas civilizações antigas
criaram seus próprios sistemas de numeração.
Um deles, criado na Índia, deu origem ao
sistema de numeração que hoje usamos. Depois
de aperfeiçoado, esse sistema apresentou
características que o tornaram mais prático que
os outros.
Vejamos tais características:

18.  As quantidades de 1 a 9 têm símbolos
diferentes para representá-las;
 O sistema é decimal ou de base 10, ou seja,
agrupamos de 10 em 10;
 Possui um símbolo (o zero) para representar
uma posição vazia no número, que pode ser a
ausência de unidade, dezenas, centenas etc;
 Com somente 10 símbolos (os algarismos) é
possível registrar todos os números, pois o
mesmo algarismo assume valor diferente de
acordo com sua posição na escrita do número.

19.  Os hindus trouxeram muitas contribuições
para a matemática. O sistema de numeração
decimal posicional é a mais conhecida delas.
 Veja como a grafia dos numerais indo-arábicos
foi se modificando com o passar do tempo:

20.  Os dez símbolos do nosso sistema de numeração são
chamados dígitos ou algarismos. Dizemos, por exemplo, que 507 é
um número de três dígitos ou três algarismos. A palavra dígito
vem da palavra latina "digitus", que significa dedo. É claro que
isto tem a ver com o uso dos dedos nas contagens. É curiosa a
origem da palavra algarismo. Durante o reinado do califa al-
Mamun, no século IX, viveu um matemático e astrônomo árabe,
que se tornou famoso. Chamava-se Mohammed ibm-Musa al-
Khowarizmi. Ele escreveu vários livros. Num deles, intitulado
"Sobre a arte hindu de calcular", ele explicava minuciosamente o
sistema de numeração hindu. Na Europa, este livro foi traduzido
para o latim e passou a ser muito consultado por aqueles que
queriam aprender a nova numeração. Apesar de al-Khowarizmi,
honestamente, explicar que a origem daquelas idéias era hindu, a
nova numeração tornou-se conhecida como a de al-Khowarizmi.
Com o tempo, o nome do matemático árabe foi modificado para
algorismi que, na língua portuguesa, acabou virando algarismo.

21. Os sistemas de numeração são de grade
importância para a humanidade. Conhecendo
cada um deles, percebemos que sua evolução
foi uma necessidade dos povos para melhor se
relacionarem, principalmente no comércio, o
que possibilita uma maior interação entre os
países.

22. ANDRINI, Álvaro Novo Praticando
Matemática. São Paulo, 2002. 1v. p. 9-13
STRVIK, Dirk J. História Concisa das
Matemáticas. Lisboa, Gradiva, 1997.
www.edu.fc.ul.pt (acesso em 17 de novembro
de 2010)
www.educart.se.usp.br/matematica