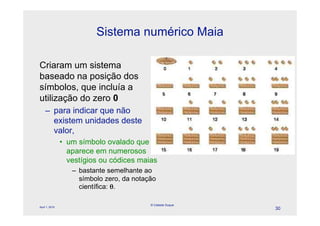
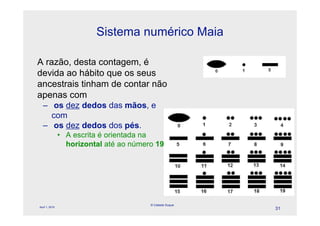
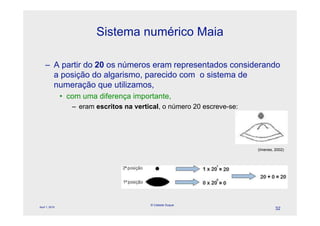
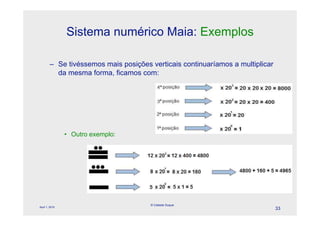
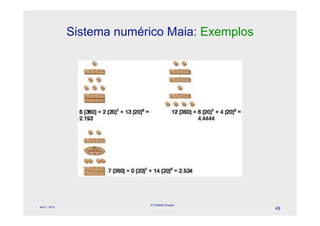
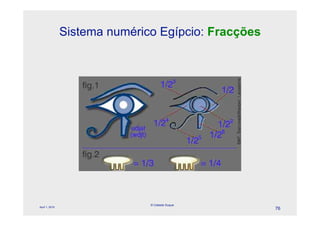
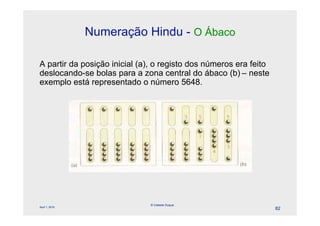
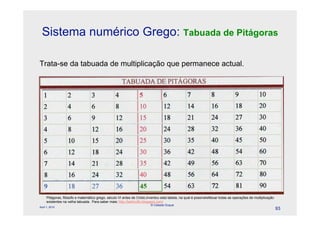
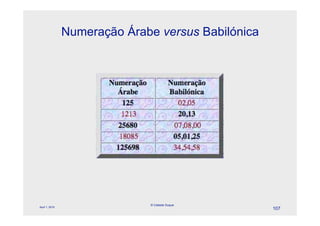
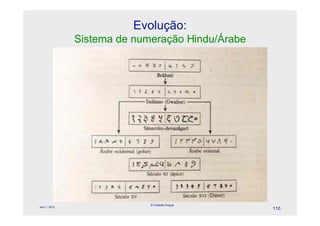
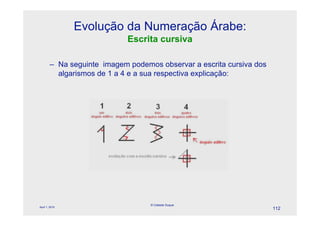
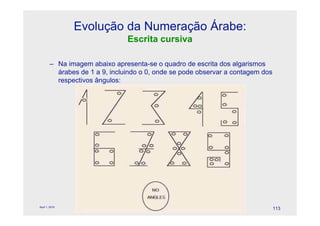
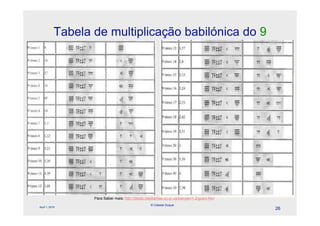
O documento descreve a evolução dos sistemas numéricos ao longo da história, começando pelas primeiras formas de contagem dos homens primitivos. Detalha os sistemas numéricos desenvolvidos por civilizações antigas como os egípcios, babilônicos e maias, mostrando como cada um desenvolveu símbolos e regras próprias para representar números.

























![Cálculo do quadrado de números
babilónicos > 59 e do cubo de números > 32
– Entre algumas das tábuas encontradas perto do rio Eufrades, datadas
de cerca de 2000 a.C., durante o período Hamurábico. Encontram-se as
que apresentavam o cálculo do quadrado de números maiores que 59. E
o Cubo de números maiores que 32.
82 = 1,4 [(1 x 601) + (4 x 600)] até chegar a
592 = 58,1 [(58 x 601) + (1 x 600)] (ver imagem).
The famous 'root (2)' tablet from the Yale
Babylonian Collection.
Para Saber mais:
http://depts.clackamas.cc.or.us/banyan/1.2/gra
nt.htm
© Celeste Duque
April 1, 2010
27](https://image.slidesharecdn.com/sistemas-numericosevolucao-120111180239-phpapp01/85/Sistemas-numericos-Evolucao-27-320.jpg)