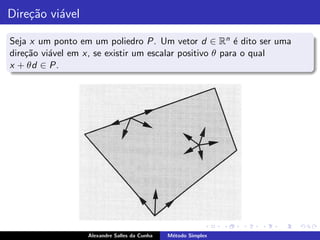
Este documento apresenta os conceitos fundamentais do método simplex para resolver problemas de programação linear. Ele explica que o método simplex se baseia no fato de que, se um problema linear possui uma solução ótima, então existe uma solução básica ótima viável. O documento também descreve como o método simplex move de uma solução básica viável para outra de menor custo, até encontrar a solução ótima.

1. M´todo Simplex
e
Alexandre Salles da Cunha
DCC-UFMG, Mar¸o 2010
c
Alexandre Salles da Cunha M´todo Simplex
e

2. Id´ias centrais do m´todo
e e
Se um PL na forma padr˜o possui uma solu¸˜o otima, ent˜o existe
a ca ´ a
uma solu¸˜o b´sica vi´vel ´tima para o problema.
ca a a o
O M´todo Simplex baseia-se neste fato. Iniciando em uma solu¸˜o
e ca
b´sica vi´vel, move-se para uma solu¸˜o b´sica vizinha de menor
a a ca a
custo.
Este processo continua at´ que uma dire¸˜o que permita reduzir a
e ca
fun¸˜o objetivo n˜o seja encontrada, comprovando a otimalidade da
ca a
solu¸˜o em m˜os.
ca a
Alexandre Salles da Cunha M´todo Simplex
e

3. O Problema a ser resolvido
min c ′x
s.t.: Ax = b
x ≥ 0
onde A ∈ Rm×n , b ∈ R
a j-´sima coluna de A ´ designada por Aj
e e
a i -´sima linha de A ´ designada por ai .
e e
Alexandre Salles da Cunha M´todo Simplex
e

4. Uma id´ia muito comum nos algoritmos de otimiza¸˜o
e ca
Dada uma solu¸˜o vi´vel, procure uma solu¸˜o vi´vel mais barata nas
ca a ca a
vizinhan¸as da solu¸˜o atual.
c ca
Esta procura de solu¸˜es vi´veis normalmente ´ feita tentando
co a e
movimentar sobre uma dire¸˜o vi´vel aprimorante.
ca a
Se uma dire¸˜o aprimorante n˜o existe, a solu¸˜o corrente ´ um
ca a ca e
o
´timo local para o problema (n˜o necess´riamente global).
a a
No caso do PL, todo ´timo local ´ global, uma vez que o PL ´ u
o e e
problema de otimiza¸˜o convexa (minimizar uma fun¸˜o conexa sobre
ca ca
um conjunto convexo).
O M´todo Simplex explora exatamente esta id´ia.
e e
Alexandre Salles da Cunha M´todo Simplex
e

5. Dire¸˜o vi´vel
ca a
Seja x um ponto em um poliedro P. Um vetor d ∈ Rn ´ dito ser uma
e
dire¸˜o vi´vel em x, se existir um escalar positivo θ para o qual
ca a
x + θd ∈ P.
Alexandre Salles da Cunha M´todo Simplex
e

6. Obtendo uma dire¸˜o vi´vel conveniente
ca a
Filosofia para escolha da dire¸˜o vi´vel
ca a
Vamos considerar a possibilidade de mover a partir de x para uma
solu¸˜o b´sica vizinha (adjacente).
ca a
Por defini¸˜o, uma solu¸˜o b´sica adjacente a x deve compartilhar
ca ca a
n − 1 restri¸˜es justas, cujos vetores de defini¸˜o s˜o l.i.
co ca a
Como as restri¸˜es ai′ x = bi , ∀i = 1, . . . m precisam ser satisfeitas em
co
qualquer solu¸˜o vi´vel, escolhemos uma dire¸˜o d para a qual
ca a ca
permitamos acrescer uma unica vari´vel n˜o b´sica.
´ a a a
Logo, para obter uma solu¸˜o b´sica adjacente a x precisarmos nos
ca a
movimentar ao longo de uma dire¸˜o vi´vel que permita que apenas
ca a
uma componente n˜o b´sica de x torne-se b´sica.
a a a
Alexandre Salles da Cunha M´todo Simplex
e

7. Dedu¸˜o alg´brica da dire¸˜o
ca e ca
Para os ´
ındices j ∈ {B(1), . . . , B(m)} das componentes n˜o b´sicas:
a a
◮ dj = 1 para uma ´nica vari´vel n˜o b´sica
u a a a
◮ dj = 0 para todas as demais vari´veis n˜o b´sicas.
a a a
◮ Vamos designar por j o ´
ındice da coluna n˜o b´sica liberado para se
a a
tornar b´sica.
a
Para os ´
ındices j ∈ {B(1), . . . , B(m)}
◮ Uma vez que A(x + θd) ∈ P para algum θ > 0, temos que
Ax + θAd = b e ent˜o Ad = 0.
a
◮ Ent˜o: 0 = Ad = n=1 Ai di = m AB(i ) di + Aj = Aj + BdB .
a i i =1
◮ Portanto dB = −B −1 Aj uma vez que B admite inversa.
Dire¸˜o b´sica
ca a
Vamos chamar a dire¸˜o b´sica constru´ acima como a j-´sima dire¸˜o
ca a ıda e ca
b´sica
a
Alexandre Salles da Cunha M´todo Simplex
e

8. E a garantia das restri¸˜es de n˜o negatividade
co a
Temos que garantir que xB + θdB ≥ 0:
Apenas uma vari´el n˜o b´sica, de ´
v a a ındice j, ser´ aumentada.
a
Logo temos que nos preocupar apenas com a varia¸˜o das vari´veis
ca a
b´sicas. Temos dois casos a considerar:
a
◮ Vamos supor que xB seja n˜o degenerada. Ent˜o xB > 0 e ent˜o existe
a a a
um θ > 0 suficientemente pequeno que garante a viabilidade.
◮ Se xB for degenerada, existe xB(i ) = 0 para algum
i ∈ {B(1), . . . , B(m)}. Neste caso, se para este ´ındice i tivermos
−Bi−1 d < 0, qualquer movimento no sentido de d faz com que a
restri¸˜o xB(i ) seja violada. Assim sendo, a dire¸˜o d neste caso n˜o ´
ca ca a e
vi´vel.
a
Alexandre Salles da Cunha M´todo Simplex
e

9. Exemplo no caso degenerado onde d n˜o ´ vi´vel
a e a
Em E (b´sica n˜o degenerada), temos como b´sicas: x2 , x4 , x5 e n´o b´sicas: x1 , x3 .
a a a a a
Dire¸ao vi´vel: segmento EF , que consiste em aumentar x1 , mantendo x3 em zero.
c˜ a
Em F (b´sica degenerada), vamos considerar que as vari´veis n˜o b´sicas sejam x3 , x5 .
a a a a
Observe que x4 ´ b´sica em 0. Dire¸ao b´sica: segmento FG , correpondendo a aumentar
e a c˜ a
x3 e manter x5 em zero, ´ n˜o ´ vi´vel.
e a e a
Alexandre Salles da Cunha M´todo Simplex
e

10. Qual o efeito na fun¸˜o objetivo de mover ao longo de d
ca
Sendo d a j-´sima dire¸˜o b´sica, ao mover no sentido positivo de d,
e ca a
a taxa de varia¸˜o da fun¸˜o objetivo ´ por n=1 ∂xi di = n=1 ci di .
ca ca e i
∂f
i
n
Uma vez que dB = −B −1 Aj temos que i =1 ci di = cj − cB B −1 Aj ,
onde cB = (cB(1) , . . . , cB(m) ).
◮ A parcela cj ´ a taxa unit´ria de varia¸˜o por permitir j aumentar.
e a ca
◮ A parcela −cB B −1 Aj ´ referente a compensa¸˜o das mudan¸as nas
e ca c
vari´veis b´sicas, necess´ria para garantir a viabilidade, Ax = b.
a a a
Defini¸˜o
ca
Seja x uma solu¸˜o b´sica, B a base associada a x e cB o vetor de custos
ca a
das vari´veis b´sicas. Para todo j = 1, . . . , n, definimos o custo reduzido
a a
c j da vari´vel xj por meio de :
a
c j = cj − cB B −1 Aj
′
Alexandre Salles da Cunha M´todo Simplex
e

11. Exemplo
Vamos considerar o seguinte exemplo:
min c1 x1 + c2 x2 + cc x3 + c4 x4
s.t.: x1 + x2 + x3 + x4 = 2
2x1 + 3x3 + 4x4 = 2
x ≥0
Fazendo B = [A1 A2 ], temos uma matriz cujas colunas s˜o l.i.
a
Fixando x3 = x4 = 0 e resolvendo o sistema, (x1 , x2 ) = (1, 1).
Assumindo que d seja a dire¸˜o b´sica associada a vari´vel n˜o b´sica
ca a a a a
x3 , temos: dB = −B −1 A3 = [− 3 2 ]′ .
2
1
c 3 = c3 − 3c1 /2 + c2 /2
Alexandre Salles da Cunha M´todo Simplex
e

12. Custo reduzido para as vari´veis b´sicas
a a
Aplicando a defini¸˜o: c B(i ) = cB(i ) − cB B −1 AB(i ) = cB(i ) − cB eB(i ) ,
ca ′ ′
onde eB(i ) ´ um vetor m dimensional com todas as entradas nulas,
e
exceto a B(i )-´sima entrada que ´ 1.
e e
′
Logo, c B(i ) = cB(i ) − cB eB(i ) = cB(i ) − cB(i ) = 0
Alexandre Salles da Cunha M´todo Simplex
e

13. Crit´rio de Otimalidade
e
Dada nossa interpreta¸˜o de custos reduzidos como a taxa de varia¸˜o da
ca ca
fun¸ao objetivo na medida em que movimentamos ao longo de uma
c˜
dire¸˜o, temos o seguinte resultado:
ca
Teorema
Considere uma solu¸˜o b´sica x associada a uma base B. Assuma que c
ca a
seja o correspondente vetor de custos reduzidos.
1 Se c ≥ 0, ent˜o x ´ uma solu¸˜o ´tima.
a e ca o
2 Se x ´ ´tima e n˜o degenerada, ent˜o c ≥ 0.
eo a a
Alexandre Salles da Cunha M´todo Simplex
e

14. Prova
Prova
(1):
Vamos assumir c ≥ 0 e que y denote uma solu¸˜o vi´vel qualquer
ca a
para o problema, para a qual determinamos uma dire¸˜o vi´vel
ca a
d = y − x (´ vi´vel por convexidade !).
e a
A viabilidade de x, y implica que Ax = Ay = b e ent˜o Ad = 0.
a
Ent˜o Ad = 0 = BdB + i ∈N Ai xi = 0 (N ´ o conj. dos ´
a e ındices das
vari´veis n˜o b´sicas em x).
a a a
Logo dB = − i ∈N B −1 Ai di
Ent˜o temos:
a
c ′ d = cB dB +
′
i ∈N ci di = i ∈N (ci − cB B −1 Ai )di =
′
i ∈N c i di .
Para qualquer i ∈ N, temos que xi = 0 e ent˜o di = yi − xi ≥ 0.
a
Logo c ′d =
i ∈N c i di ≥ 0
Alexandre Salles da Cunha M´todo Simplex
e

15. Prova
Prova
(2), por contradi¸˜o:
ca
Suponha que x seja uma solu¸˜o b´sica vi´vel ´tima, n˜o degenerada
ca a a o a
e que exista j : c j < 0.
Ent˜o j necessariamente deve ser ´
a ındice de uma vari´vel n˜o b´sica,
a a a
uma vez que c i = 0, ∀i ∈ {B(1), . . . , B(m)}.
Considere a dire¸˜o b´sica j, d. Esta dire¸˜o ´ necessariamente vi´vel
ca a ca e a
dado que x ´ n˜o degenerada.
e a
Ent˜o existe θ > 0 tal que x + θd ´ uma solu¸˜o vi´vel. Por outro
a e ca a
lado c ′ (x + θd) = c ′ x + θc ′ d < c ′ x, contrariando a hip´tese de que x
o
´ ’otima.
e
Alexandre Salles da Cunha M´todo Simplex
e

16. Observa¸˜es
co
Uma solu¸˜o ´tima x pode ser tal que o custo reduzido de alguma
ca o
vari´vel n˜o b´sica ´ negativo.
a a a e
De acordo com o teorema para decidir se uma solu¸˜o b´sica vi´vel
ca a a
n˜o degenerada x ´ ´tima, precisamos verificar os custos reduzidos de
a eo
suas n − m componentes n˜o b´sicas.
a a
No caso de uma solu¸˜o b´sica degenerada, um teste igualmente
ca a
simples n˜o ´ dispon´
a e ıvel.
Alexandre Salles da Cunha M´todo Simplex
e

17. Bases ´timas
o
Defini¸˜o
ca
Uma base B ´ ´tima se:
eo
1 B −1 b ≥ 0 e
2 c ′ = c ′ − cB B −1 B −1 A ≥ 0.
′
Observe que, diante desta defini¸˜o:
ca
Se uma base ´tima B ´ encontrada, a solu¸˜o b´sica associada ´
o e ca a e
vi´vel, satisfaz as condi¸˜es de otimalidade e portanto ´ ´tima.
a co eo
Por outro lado uma solu¸˜o b´sica vi´vel ´tima degenerada n˜o
ca a a o a
necessariamente garante custos reduzidos n˜o negativos.
a
Vale lembrar que mais de uma base podem ser associadas ` mesma
a
solu¸˜o b´sica (no caso degenerado).
ca a
Alexandre Salles da Cunha M´todo Simplex
e

18. Desenvolvimento do m´todo
e
De in´
ıcio, vamos assumir a hip´tese de que todos as solu¸˜es b´sicas
o co a
de P = {x ∈ Rn : Ax = b, x ≥ 0} s˜o n˜o degeneradas.
a a
Em seguida relaxaremos esta hip´tese.
o
Alexandre Salles da Cunha M´todo Simplex
e

19. Desenvolvimento do M´todo
e
Vamos supor que estejamos em um ponto x, solu¸˜o b´sica vi´vel
ca a a
n˜o degenerada de P e que tenhamos avaliado os custos reduzidos de
a
forma que c j ≥ 0 : ∀j ∈ {B(1), . . . , B(m)}. Ent˜o, pelo resultado
a
anterior, concluimos que x resolve o PL.
Caso contr´rio, existe j ∈ {B(1), . . . , B(m)} : c j < 0.
a
Ent˜o a j−´sima dire¸˜o b´sica d, obtida fazendo-se dB = −B −1 Aj ,
a e ca a
dj = 1 e dk = 0, ∀k ∈ {j, B(1), . . . , B(m)} ´ uma dire¸˜o vi´vel, de
e ca a
redu¸˜o de custo.
ca
Movendo ao longo de d, a partir de x, a componente xj torna-se
positiva, as componentes xk : k ∈ {j, B(1), . . . , B(m)} permanecem
em 0 e as vari´veis b´sicas s˜o alteradas.
a a a
Uma vez que d ´ uma dire¸˜o de aprimoramento de custos, ´
e ca e
desej´vel nos mover o quanto pudermos ao longo desta dire¸˜o.
a ca
Alexandre Salles da Cunha M´todo Simplex
e

20. Garantindo a satisfa¸˜o das restri¸˜es de n˜o negatividade
ca co a
x(θ) = x + θd, θ ≥ 0
O m´ximo que podemos andar na dire¸˜o d ´ dado por
a ca e
θ ∗ = max{θ ≥ 0 : x + θd ∈ P}.
Dado que Ad = 0, Ax(θ) = b e precisamos verificar apenas as
restri¸˜es de n˜o negatividade.
co a
Se d ≥ 0, x(θ) ≥ 0 e ent˜o θ ∗ = ∞.
a
Caso contr´rio, existe i ∈ {B(1), . . . , B(m)} : di < 0. Para garantir
a
x
xi + θdi ≥ 0 temos que θ ≤ − dii .
x
Ent˜o θ ∗ = min{− dii : dB(i ) < 0}
a
Observe que θ ∗ > 0 como consequˆncia da n˜o degenera¸˜o de x.
e a ca
Alexandre Salles da Cunha M´todo Simplex
e

21. O novo ponto obtido
Assumindo que θ ∗ ´ finito, y = x(θ ∗ ) = x + θ ∗ d.
e
Ent˜o:
a
x
yj = xj + θ ∗ = − dB(l ) , onde l ∈ {B(1), . . . , B(m)} denota o ´
B(l )
ındice da
vari´vel b´sica que definiu θ
a a ∗.
Todas as componentes b´sicas de x, pelo modo como θ ∗ ´ definido
a e
continuam n˜o negativas.
a
Em particular, para l temos:
xB(l)
yB(l) = xB(l) + θdB(l) = xB(l) − d =0
dB(l) B(l)
o que sugere que a coluna Aj substitua a coluna AB(l) na base, uma
vez que houve uma troca das restri¸˜es de n˜o negatividade que
co a
ficaram justas.
Alexandre Salles da Cunha M´todo Simplex
e

22. Exemplo - continua¸˜o
ca
Considerando a solu¸˜o b´sica x = (1, 1, 0, 0) e lembrando que
ca a
c2
c 3 = −3c1 + 2 + c3 .
Se c = (2, 0, 0, 0) temos que c 3 = −3. A correspondente dire¸˜o
ca
3 1
b´sica ´ (− 2 , 2 , 1, 0).
a e
Considerando pontos da forma x + θd, θ > 0, a unica componente de
´
x
x que cai ´ x1 (note que d1 < 0) e portanto θ ∗ = − d1 = 2 .
e 1 3
O novo ponto obtivo ´ y = x + 2 d = (0, 3 , 2 , 0).
e 3
4
3
Observe que as novas colunas associadas `s vari´veis b´sicas (x2 , x3 )
a a a
s˜o l.i..
a
Alexandre Salles da Cunha M´todo Simplex
e

23. A nova base
A nova base B ´ dada por:
e
B = [AB(1) , . . . , AB(l−1) , AB(j) , AB(l+1) , . . . , AB(m) ]
Equivalentemente, o novo conjunto de vari´veis b´sicas ´
a a e
{B(1), . . . , B(l − 1), B(j), B(l + 1), . . . , B(m)}
Mais formalmente:
Teorema
1 As colunas AB(i ) : i = l e Aj s˜o linearmente independentes e, assim,
a
B ´ uma matriz b´sica.
e a
2 O vetor y = x + θ ∗ d ´ a solu¸˜o b´sica associada a B.
e ca a
Alexandre Salles da Cunha M´todo Simplex
e

24. Prova
Prova
(1): por contradi¸˜o:
ca
Vamos supor que os vetores AB(i ) sejam l.d. Ent˜o, existem
a
coeficientes λ1 , . . . , λm , n˜o todos nulos, tais que m λi AB(i ) = 0.
a i =1
−1 temos m
Multiplicando por B i =1 λi B −1 AB(i ) = 0 e os vetores
B −1 AB(i ) tamb´m s˜o l.d. Vamos mostrar que este n˜o ´ o caso.
e a a e
Observe que B −1 B = I . Logo B −1 AB(i ) = ei , i = l (ei denota o vetor
de zeros, exceto na i´sima entrada, que ´ 1). Todos os vetores
e e
B −1 AB(i ) possuem um 0 na l −´sima entrada. Logo, B −1 AB(i ) , i = l
e
s˜o l.i..
a
Por outro lado B −1 AB(l) = B −1 Aj = −dB .
Por defini¸˜o, dB(l) < 0. Logo B −1 Aj e B −1 AB(i ) , i = l s˜o l.i..
ca a
Logo, B ´ uma base.
e
Alexandre Salles da Cunha M´todo Simplex
e

25. Prova
Prova
(2):
Temos que y ≥ 0, Ay = b.
Al´m disto yi = 0, ∀i ∈ {B(i ), . . . , B(i )}.
e
Acabamos de mostrar que AB(i ) , . . . , AB(i ) s˜o l.i..
a
Portanto, segue que y ´ uma solu¸˜o b´sica associada a B
e ca a
Alexandre Salles da Cunha M´todo Simplex
e

26. Observa¸˜es
co
Uma vez que θ ∗ > 0, segue que y ´ uma solu¸˜o b´sica distinta de x,
e ca a
uma vez que d ´ uma dire¸˜o de redu¸˜o de custos e ent˜o c ′ y < c ′ x.
e ca ca a
Em parte, cumprimos nosso prop´sito inicial de mover para uma
o
solu¸˜o b´sica adjacente, de menor custo.
ca a
Vamos enunciar uma itera¸˜o t´ ca ıpica do M´todo Simplex, definindo
e
um vetor u = (u1 , . . . , um ), de forma que u = −dB = B −1 Aj , onde Aj
´ a coluna que entra na base. Ou seja, ui = −dB(i ) : i = 1, . . . , m.
e
Alexandre Salles da Cunha M´todo Simplex
e

27. M´todo Simplex: Itera¸˜o T´
e ca ıpica
1 Inicie a itera¸˜o com as colunas b´sicas B(1), . . . , B(m) e a solu¸˜o
ca a ca
b´sica vi´vel associada x. Seja N o conjunto dos ´
a a ındices das vari´veis
a
n˜o b´sicas.
a a
2 Calcule os custos reduzidos c j = cj − cB B −1 Aj , ∀j ∈ N. Se c ≥ 0,
′
p´re, a solu¸˜o x ´ ´tima. Caso contr´rio, escolha j ∈ N : c j < 0.
a ca eo a
3 Calcule u = B −1 Aj . Se u ≤ 0, temos que θ ∗ = ∞ e o custo ´timo ´
o e
−∞. P´re, o problema ´ ilimitado.
a e
xB(i )
4 Se alguma componente de u ´ positiva, fa¸a θ ∗ = mini ∈1,...,m:ui >0
e c ui .
Seja l tal que θ ∗ = xB(l ) .
ul
5 Forme uma nova base substituindo AB(l) por Aj . Denote por y a nova
solu¸˜o b´sica vi´vel. Ent˜o yj = θ ∗ e yB(i ) = xB(i ) − θ ∗ ui , i l .
ca a a a
Alexandre Salles da Cunha M´todo Simplex
e

28. Na ausˆncia de degenera¸˜o, O M´todo Simplex converge
e ca e
Teorema
Assuma que o conjunto de solu¸˜es vi´veis do PL ´ n˜o vazio e que toda
co a e a
solu¸˜o b´sica ´ n˜o degenerada. Ent˜o, o M´todo Simplex termina ap´s
ca a e a a e o
um n´mero finito de itera¸˜es. Ao final, temos duas possibilidades:
u co
1 Dispomos de uma base ´tima B e a correspondente solu¸˜o b´sica
o ca a
o
´tima.
2 Encontramos um vetor d : Ad = 0, d ≥ 0 e c ′ d < 0. Portanto o custo
o
´timo ´ −∞.
e
Alexandre Salles da Cunha M´todo Simplex
e

29. Prova
Prova
Se o algoritmo termina no passo 2, as condi¸˜es de otimalidade
co
propostas previamente foram satisfeitas e B ´ uma base ´tima.
e o
Se o algoritmo termina no passo 3, estamos em uma solu¸˜o b´sica x
ca a
e descobrimos uma vari´vel n˜o b´sica xj tal que c j < 0. A j−´sima
a a a e
dire¸˜o b´sica j satisfaz Ad = 0, d ≥ 0. Em particular temos que
ca a
x + θd ∈ P para θ t˜o grande quanto queiramos. Uma vez que
a
c ′ d = c j , o custo pode ser feito t˜o negativo quanto queiramos.
a
Em cada itera¸˜o do algoritmo, nos movemos uma quantidade θ ∗ > 0
ca
ao longo de uma dire¸˜o b´sica d satisfazendo c ′ d < 0. Assim sendo,
ca a
a cada itera¸˜o o custo diminui e portanto n˜o visitamos a mesma
ca a
solu¸˜o b´sica mais de uma vez.
ca a
Como o n´mero de solu¸˜es b´sicas ´ finito, o algoritmo ent˜o
u co a e a
termina.
Alexandre Salles da Cunha M´todo Simplex
e

30. M´todo Simplex para problemas degenerados
e
Vamos considerar a partir de agora, como se comporta o algoritmo
descrito anteriormente, diante da degenera¸˜o:
ca
1 Se a solu¸˜o b´sica corrente x for degenerada, θ ∗ pode ser nulo, caso
ca a
xB(l) = 0 e dB(l) < 0. Por este motivo, a nova solu¸˜o obtida y ´
ca e
idˆntica a x. Ainda assim, podemos definir uma nova matriz B com a
e
entrada da coluna Aj e a sa´ de AB(l) de forma que B ser´ uma
ıda a
base.
2 Mesmo se θ ∗ > 0, pode acontecer de mais de uma vari´vel b´sica se
a a
tornar zero no novo ponto x + θ ∗ d. Uma vez que apenas uma destas
vari´veis b´sicas que se tornou nula sair´ da base para a entrada da
a a a
coluna Aj , a nova solu¸˜o encontrada y = x + θ ∗ d ser´ degenerada.
ca a
Alexandre Salles da Cunha M´todo Simplex
e

31. Efeito da degenera¸˜o
ca
As mudan¸as de base associadas ` mesma solu¸ao b´sica podem, em
c a c˜ a
alguns casos, n˜o ser in´teis, levando a descobrir uma dire¸˜o b´sica
a u ca a
de redu¸˜o de custo.
ca
Por outro lado, uma sequˆncia de mudan¸as de base associadas ao
e c
mesmo ponto x pode levar ` repeti¸˜o das colunas associadas `
a ca a
representa¸˜o da base, ocasionando a ciclagem.
ca
Para problemas altamente estruturados (fluxo em redes, etc) a
possibilidade n˜o ´ remota.
a e
A ciclagem pode ser evitada atrav´s do uso de regras adequadas de
e
quais vari´veis entrar˜o e/ou sair˜o da base.
a a a
Alexandre Salles da Cunha M´todo Simplex
e

32. Ilustra¸˜o dos dois casos em uma solu¸˜o degenerada
ca ca
Neste exemplo temos n − m = 2. Vale observar a solu¸˜o degenerada x.
ca
Alexandre Salles da Cunha M´todo Simplex
e

33. O M´todo Simplex pode n˜o terminar ?
e a
Quadro 1, B = {5, 6, 7}, entra x1 , sai x5
x5 = − 0.5x1 + 5.5x2 + 2.5x3 − 9x4
x6 = − 0.5x1 + 1.5x2 + 0.5x3 − x4
x7 = 1 − x1
z = + 10x1 − 57x2 − 9x3 − 24x4
Quadro 2, B = {1, 6, 7}, entra x2 , sai x6
x1 = + 11x2 + 5x3 − 18x4 − 2x5
x6 = − 4x2 − 2x3 + 8x4 + x5
x7 = 1 − 11x2 − 5x3 + 18x4 + 2x5
z = + 53x2 + 41x3 − 204x4 − 20x5
Alexandre Salles da Cunha M´todo Simplex
e

34. O M´todo Simplex pode n˜o terminar ?
e a
Quadro 3, B = {1, 2, 7}, entra x3 , sai x1
x2 = − 0.5x3 + 2x4 + 0.25x5 − 0.25x6
x1 = − 0.5x3 + 4x4 + 0.75x5 − 2.75x6
x7 = 1 + 0.5x3 − 4x4 − 0.75x5 − 13.25x6
z = + 14.5x3 − 98x4 − 6.75x5 − 13.25x6
Quadro 4, B = {2, 3, 7}, entra x4 , sai x2
x3 = + 8x4 + 1.5x5 − 5.5x6 − 2x1
x2 = − 2x4 − 0.5x5 + 2.5x6 + x1
x7 = 1 − x1
z = + 18x4 + 15x5 − 93x6 − 29x1
Alexandre Salles da Cunha M´todo Simplex
e

35. O M´todo Simplex pode n˜o terminar ?
e a
Quadro 5, B = {3, 4, 7}, entra x5 , sai x3
x4 = − 0.25x5 + 1.25x6 + 0.5x1 − 0.5x2
x3 = − 0.5x5 + 4.5x6 + 2x1 − 4x2
x7 = 1 − x1
z = + 10.5x5 − 70.5x6 − 20x1 − 9x2
Quadro 6, B = {4, 5, 7}, entra x6 , sai x4
x5 = + 9x6 + 4x1 − 8x2 − 2x3
x4 = − x6 − 0.5x1 + 1.5x2 + 0.5x3
x7 = 1 − x1
z = + 24x6 + 22x1 − 93x2 − 21x3
Alexandre Salles da Cunha M´todo Simplex
e

36. O M´todo Simplex pode n˜o terminar ? Sim, caso cicle.
e a
O pr´ximo quadro ´ igual ao quadro inicial !
o e
Quadro 7, B = {5, 6, 7}, entra x1 , sai x5
x6 = − 0.5x1 + 1.5x2 + 0.5x3 − x4
x5 = − 0.5x1 + 5.5x2 + 2.5x3 − 9x4
x7 = 1 − x1
z = + 10x1 − 57x2 − 9x3 − 24x4
Alexandre Salles da Cunha M´todo Simplex
e

37. Possibilidades para implementar o pivoteamento
At´ o momento, n˜o particularizamos regra alguma para escolher as
e a
regras de pivoteamento, isto ´, escolher qual vari´vel entra e sai da
e a
base. Em particular, na descri¸˜o que apresentamos do M´todo Simplex,
ca e
temos flexibilidade quanto ` escolha de:
a
1 Qual coluna n˜o b´sica com custo reduzido ´ negativo deve ser eleita
a a e
para entrar na base;
2 Diante de mais de uma vari´vel que definam θ ∗ , qual escolher para
a
deixar a base.
Alexandre Salles da Cunha M´todo Simplex
e

38. Algumas prov´veis candidatas a regras de pivotemento :
a
Escolher para entrar na base, a coluna n˜o b´sica Aj que possui o
a a
custo reduzido c j mais negativo.
Escoher para entrar na base, a coluna n˜o b´sica Aj que promova o
a a
maior redu¸˜o na fun¸˜o objetivo, isto ´ θ ∗c j . Esta regra pode
ca ca e
acelerar a queda da fun¸˜o objetivo, mais paga-se maior pre¸o
ca c
computacional, para se avaliar o θ ∗ associado a entrada de cada
coluna que possua c j . A experiˆncia computacional existe sugere que
e
o tempo global de cpu n˜o decresce com a ado¸˜o desta estrat´gia.
a ca e
Mesmo a primeira estrat´gia acima pode ser muito cara para
e
problemas de larga escala (requer que todas as colunas tenham seus
custos reduzidos avaliados). Assim sendo, uma regra simples consiste
na regra de escolher a coluna com custo reduzido negativo, de menor
´
ındice.
Alexandre Salles da Cunha M´todo Simplex
e

39. Implementa¸˜es do Simplex
co
Os vetores B −1 Aj s˜o de fundamental importˆncia no algoritmo, uma
a a
vez que com estas informa¸˜es podemos obter:
co
◮ Custos reduzidos c j = cj − cB B −1 Aj
′
◮ A dire¸˜o de busca d
ca
◮ O valor de θ∗
Por este motivo, a diferen¸a entre as implementa¸˜es alternativas do
c co
M´todo Simplex residem em como esta informa¸˜o ´ calculada e
e ca e
quais informa¸˜es s˜o preservadas de itera¸˜o para itera¸˜o.
co a ca ca
Dado que B ´ uma matriz m × m temos:
e
◮ Custo de resolver Bx = b: O(m3 )
◮ Custo de efetuar a mutiplica¸˜o Bb: O(m2 )
ca
◮ Custo de calcular o produto interno de dois vetores m dimensionais:
O(m).
Alexandre Salles da Cunha M´todo Simplex
e

40. Implmenta¸˜o Inocente
ca
1 Nenhuma informa¸˜o adicional ser´ transportada de itera¸˜o para
ca a ca
itera¸˜o no m´todo.
ca e
2 Em cada itera¸˜o t´
ca ıpica, conhecemos os ´
ındices B(1), . . . , B(m) das
vari´veis b´sicas.
a a
3 Montamos a matriz B e resolvemos o sistema linear p ′ B = cB .
′
4 O custo reduzido para qualquer coluna j ´ obtido via c j = cj − p ′ Aj .
e
5 Dependendo da regra de pivoteamento adotado, podemos evitar
calcular todos os custos reduzidos.
6 Uma vez que escolhemos a coluna Aj para entrar na base, resolvemos
Bu = Aj (ou u = B −1 Aj ).
7 A partir de ent˜o, podemos calcular θ ∗ e definir qual vari´vel sair´ da
a a a
base.
Alexandre Salles da Cunha M´todo Simplex
e

41. Implementa¸˜o inocente - complexidade computacional
ca
Resolver os sistemas lineares (p ′ B = cB e u = B −1 Aj ): O(m3 ).
′
Dependendo da estrutura da matriz B, este custo pode ser reduzido
sensivelmente (exemplo: Problemas de Fluxo em Redes)
C´lculo do custo reduzido para todas as colunas: O(mn)
a
Custo total por itera¸˜o: O(nm + m3 ).
ca
Veremos como fazer a itera¸˜o a um custo de O(m2 + mn)
ca
Alexandre Salles da Cunha M´todo Simplex
e

42. Simplex Revisado
Boa parte do custo computacional por itera¸˜o ´ relacionado `
ca e a
resolu¸˜o de dois sistemas lineares.
ca
Neste m´todo, a matriz B −1 ´ explicitamente mantida em cada
e e
itera¸˜o e os vetores cB B −1 e B −1 Aj s˜ determinados via
ca ′ a
multiplica¸˜o matricial.
ca
Para ser eficiente, o m´todo requer um esquema eficiente de
e
atualiza¸˜o de B
ca −1 quando implementarmos uma opera¸˜o de
ca
pivoteamento.
Alexandre Salles da Cunha M´todo Simplex
e

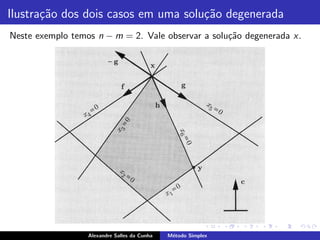
43. Simplex Revisado
Base no in´ da itera¸˜o: B = [AB(1) , . . . , AB(m) ]
ıcio ca
Base ao fim da itera¸˜o: ca
B = [AB(1) , . . . , AB(l−1) , AB(j) , AB(l+1) , . . . , AB(m) ]
Todas, exceto uma coluna de B e B s˜o compartilhadas.
a
Em fun¸˜o disto, ´ razo´vel esperar que B −1 contenha informa¸˜o
ca e a ca
−1
que possa ser usada na determina¸˜o de B .
ca
Alexandre Salles da Cunha M´todo Simplex
e

44. −1
Como aproveitar informa¸˜es de B −1 para avaliar B
co
Defini¸˜o
ca
Dada uma matriz, n˜o necessariamente quadrada, a opera¸ao de adicionar
a c˜
um m´ltiplo de uma linha ` mesma linha ou a outra linha da matriz ´
u a e
chamada de opera¸˜o linha elementar (n˜o muda as informa¸˜es dos
ca a co
sistemas lineares representados pela matriz).
Exemplo
Digamos que queiramos multiplicar a terceira linha da matriz C abaixo por
2 para somar ` primeira linha da matriz. Isto equivale a multiplicar C pela
a
matriz Q dada abaixo.
     
1 2 1 0 2 11 14
C =  3 4  Q =  0 1 0  QC =  3 4 
5 6 0 0 1 5 6
Alexandre Salles da Cunha M´todo Simplex
e

45. Generalizando este exemplo
Multiplicar a j−´sima linha de uma matriz por β e adicionar este
e
produto ` i −´sima linha da matriz, equivale a pr´ mutiplicar a matriz
a e e
por Q = I + Dij , onde Dij ´ uma matriz de zeros, exceto em sua
e
entrada na i −´sima linha e j−´sima coluna que ´ β.
e e e
Observe que a matriz Q possui determinante 1 e ent˜o admite inversa.
a
Suponha que queiramos fazer uma sequˆncia de K opera¸˜es linha
e co
elementares, cada qual correspondento a pr´-multiplica¸˜o por uma
e ca
matriz Qk correspondente. Esta sequˆncia de opera¸˜es consiste em
e co
pr´ multiplicar a matriz sobre a qual s˜o feitas as opera¸˜es por:
e a co
QK QK −1 . . . Q2 Q1 .
Alexandre Salles da Cunha M´todo Simplex
e

46. Aplicando esta id´ia no M´todo Simplex
e e
Uma vez que B −1 B = I , temos que B −1 AB(i ) = ei , onde ei ´ um
e
vetor de zeros exceto pela i −´sima entrada que ´ 1.
e e
 
1 u1
.. .
. .
 

 . 

Usando esta observa¸˜o temos B
ca −1 B =  ul 
. ..
 

 .
. .


um 1
Para transformar a matriz acima na identidade:
◮ Para cada i = l, adicionamos o produto da l− ´sima linha (linha pivot)
e
por −ui e somamos ` i− ´sima linha. Observe que ul = 0 e ent˜o esta
ul a e a
opera¸˜o substitui ui por 0 na correspondente i−´sima linha.
ca e
◮ Dividimos a l− ´sima linha por ul .
e
Seja Q o produto destas m opera¸˜es linha elementares. Temos ent˜o
co a
que QB −1 B = I , logo B −1 = QB −1 .
Alexandre Salles da Cunha M´todo Simplex
e

47. Exemplo
Vamos considerar l = 3 (a terceira coluna de B ser´ alterada para
a
compor B) e
   
1 2 3 −4
−1
B =  −2 3 1 u =  2 
4 −3 −2 2
   
1 0 2 9 −4 −1
−1
Ent˜o temos: Q =  0 1 −1  B =  −6
a 6 3 
1
0 0 2 2 −1.5 −1
Alexandre Salles da Cunha M´todo Simplex
e

48. M´todo Simplex Revisado
e
Vamos adicionar o seguinte passo ao final da quinta opera¸˜o na itera¸˜o
ca ca
t´
ıpica:
Forme a matriz m × (m + 1) dada por: [B −1 | u].
Fa¸a as opera¸˜es linha elementares necess´rias para transformar a
c co a
ultima coluna desta matriz no vetor unit´rio el .
´ a
−1
As primeiras m colunas da matriz resultante fornece B .
Observe que recalcular a inversa da base agora custa O(m2 ). Desta forma,
apenas na primeira invers˜o da base, pagamos o O(m3 ). Desta forma,
a
reduzimos o custo de cada itera¸˜o para O(nm + m2 )
ca
Alexandre Salles da Cunha M´todo Simplex
e

49. Regras anti-ciclagem
Regra lexicogr´fica, adequada ` implementa¸˜o da vers˜o Full table
a a ca a
implementation que, por ter o comportamento assint´tico pior que a
o
vers˜o do Simplex Revisado, n˜o ser´ discutida.
a a a
Regra de Bland - compat´ com a implementa¸˜o do Simplex
ıvel ca
Revisado.
Alexandre Salles da Cunha M´todo Simplex
e

50. Regra de Bland
Pivoteamento de Bland
1 Encontre o menor ´
ındice j para o qual o custo reduzido c j ´ negativo.
e
2 Dentre as vari´veis b´sicas xi que se anularem primeiro com o
a a
incremento da vari´vel xj (para as quais houver empate na
a
determina¸˜o de θ ∗ ), escolha aquela com o menor ´
ca ındice i .
Observa¸˜es:
co
Esta regra n˜o nos obriga a calcular todos os custos reduzidos.
a
´
E compat´el com a implementa¸˜o do Simplex Revisado, na qual os
v ca
custos reduzidos s˜o calculados na ordem natural das vari´veis.
a a
Diante desta regra ´ provado que n˜o pode haver ciclagem e o
e a
M´todo Simplex converge ap´s um n´merol finito de mudan¸as de
e o u c
base.
Alexandre Salles da Cunha M´todo Simplex
e

51. Encontrando uma base inicial vi´vel
a
No M´todo Simplex, assumimos dispor de uma solu¸˜o b´sica vi´vel
e ca a a
inicial. N˜o descrevemos ainda como obter esta solu¸ao.
a c˜
Em alguns casos, encontrar esta solu¸˜o ´ trivial. Exemplo:
ca e
P ′ = {x ∈ Rn : Ax ≤ b} e o vetor b ≥ 0. Neste caso, introduzindo as
+
n m
vari´veis de folga temos P = {(x, s) ∈ (R+ , R+ ) : Ax + Is = b} e o
a
vetor (x, s) = (0, b) ´ uma solu¸˜o b´sica vi´vel.
e ca a a
De um modo geral, encontrar esta solu¸˜o n˜o ´ t˜o trivial,
ca a e a
requerendo a solu¸˜o de um problema linear auxiliar (Fase 1).
ca
Alexandre Salles da Cunha M´todo Simplex
e

52. Constru¸˜o de um problema auxiliar
ca
Problema Original
min c ′x
Ax = b
x ≥0
Assumimos sem perda de generalidade que b ≥ 0 (caso contr´rio,
a
multiplicamos alguma linha do sistema linear por −1)
Alexandre Salles da Cunha M´todo Simplex
e

53. Constru¸˜o de um problema auxiliar - Fase 1
ca
Problema Auxiliar (PA)
m
min yi
i =1
Ax + y = b
x ≥0
y ≥0
Introduzimos as vari´veis artificiais y ∈ Rm +.
a
Uma solu¸˜o b´sica inicial para o Prob. Auxiliar ´ dada por
ca a e
(x, y ) = (0, b).
Resolvemos PA. Se a fun¸˜o objetivo ´tima for 0 sabemos que h´
ca o a
solu¸˜o vi´vel para o problem original. Caso contr´rio, o problema
ca a a
original ´ invi´vel.
e a
Como obter a solu¸˜o b´sica inicial para o problema original ?
ca a
Alexandre Salles da Cunha M´todo Simplex
e

54. Obtendo uma solu¸˜o vi´vel inicial a partir de PA
ca a
Para iniciar o M´todo Simplex, necessitamos de uma solu¸˜o b´sica inicial
e ca a
e a matriz b´sica associada. Vamos assumir que no ´timo de PA tenhamos
a o
m
j=1 yj = 0 (prob. original ´ vi´vel).
e a
Analisando a solu¸˜o do PA:
ca
1 Se ao final da resolu¸˜o de PA as colunas b´sicas na solu¸ao ´tima
ca a c˜ o
forem exclusivamente as vari´veis x, basta tomarmos esta solu¸˜o
a ca
como uma sol. b´sica vi´vel inicial (e as correspondentes colunas
a a
compondo a base) para iniciar o problema original.
2 Se existirem vari´veis yj b´sicas (necessariamente degeneradas) na
a a
solu¸˜o ´tima de PA, devemos fazer opera¸˜es de pivoteamento
ca o co
for¸ado para removˆ-las da base.
c e
Alexandre Salles da Cunha M´todo Simplex
e

55. Eliminando as vari´veis y para fora da base
a
Vamos supor (como de costume) que posto(A) = m.
Vamos assumir que k < m colunas de A aparecem na base ´tima de o
PA. Os ´ ındices das vari´veis b´sicas associadas a estas colunas s˜o
a a a
B1 , . . . , Bk
Vale observar que as colunas AB(1) , . . . , AB(k) s˜o linearmente
a
independentes, uma vez que est˜o na base.
a
Como a matriz A ∈ Rm×n possui posto m, suas colunas geram o
espa¸o Rm . Logo, ´ poss´ escolher outras m − k colunas de A, que
c e ıvel
sejam linearmente independentes a AB(1) , . . . , AB(k) .
Vamos identificar estas colunas, eliminando as colunas associadas a y
da base.
Alexandre Salles da Cunha M´todo Simplex
e

56. Eliminando as vari´veis artificiais
a
Vamos supor que a l −´sima (l > k) vari´vel b´sica seja artificial.
e a a
Dentre as vari´veis xj : j ∈ {B(1), . . . , B(m)}, procuramos uma
a
coluna j tal que B −1 Aj = 0.
Claramente Aj ´ l.i. com AB(1) , . . . , AB(k) (por quˆ ?)
e e
Ent˜o fazemos um pivoteamento for¸ado, no qual trazemos a coluna
a c
Aj para a base e eliminados a coluna da vari´vel artificial da base.
a
Repetimos o processo enquanto houver colunas b´sicas associadas a
a
vari´veis artificiais.
a
Alexandre Salles da Cunha M´todo Simplex
e

57. Complexidade computacional do m´todo simplex
e
A complexidade do m´todo Simplex depende:
e
1 da complexidade computacional em cada itera¸˜o (O(nm), por
ca
exemplo, no caso do Simplex Revisado)
2 do n´mero de itera¸˜es, ou opera¸˜es de pivoteamento.
u co co
Na pr´tica: ao longo dos anos observou-se que o m´todo
a e
normalmente executa O(m) opera¸˜es de pivoteamento na m´dia.
co e
Pior caso: esta observa¸˜o que ocorre na pr´tica n˜o ´ verdadeira
ca a a e
para qualquer Programa Linear e qualquer regra de pivoteamento. H´a
exemplos de problemas n˜o degenerados nos quais o m´todo percorre
a e
todos os v´rtices do poliedro at´ encontrar a solu¸˜o ´tima.
e e ca o
Alexandre Salles da Cunha M´todo Simplex
e

58. Complexidade no pior caso
Vamos considerar o problema de minimizar −xn sobre o cubo
P = {x ∈ Rn : 0 ≤ xi ≤ 1, i = 1 dots, n}. Estes cubo possui 2n
v´rtices, metade dos quais possuem custo 0 e a outra metade custo
e
−1. Assim sendo, a fun¸˜o objetivo n˜o pode decrescer
ca a
monotonicamente ao longo das itera¸˜es do Simplex.
co
Por este motivo, vamos perturbar o cubo, mantendo o n´mero de
u
v´rtices, impondo as seguintes restri¸˜es, para ǫ ∈ (0, 1 )
e co 2
ǫ ≤ x1 ≤ 1,
ǫxi −1 ≤ xi ≤ 1 − xi −1 , i = 2, . . . , n
de forma a criar uma sequˆncia de v´rtices adjacentes para os quais a
e e
fun¸ao objetivo seja reduzida quando nos movemos de um v´rtice para o
c˜ e
outro.
Alexandre Salles da Cunha M´todo Simplex
e

59. Criamos um caminho que percorre todos os v´rtices
e
Existe uma regra de pivoteamento que faz o m´todo percorrer todos os
e
v´rtices (ver a prova em Papadimitrou e Steiglitz, pp. 166-170).
e
min −xn
ǫ ≤ x1 ≤ 1,
ǫxi −1 ≤ xi ≤ 1 − xi −1 , i = 2, . . . , n
Alexandre Salles da Cunha M´todo Simplex
e

60. Existe regra de pivoteamento imune a esta patologia ?
Quest˜o em aberto
a
Para v´rias regras populares de pivotemento, h´ exemplos como o
a a
indicado anteriormente, que fazem o m´todo percorrer todos os
e
v´rtices.
e
Entretanto, estes exemplos n˜o excluem a possibilidade de existir uma
a
regra de pivotemento que n˜o apresente o comportamento de pior
a
caso exponencial.
Esta ´ uma das quest˜es mais importantes em Teoria de Programa¸˜o
e o ca
Linear, ainda em aberto.
O fato ´ que n˜o se conhece uma regra de pivoteamento imune a esta
e a
patologia.
O Problema de Programa¸˜o Linear ´ polinomialmente sol´vel
ca e u
(Algoritmo do Elips´ide).
o
Alexandre Salles da Cunha M´todo Simplex
e