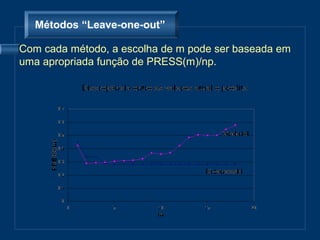
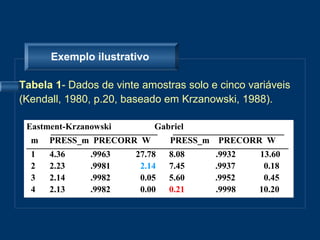
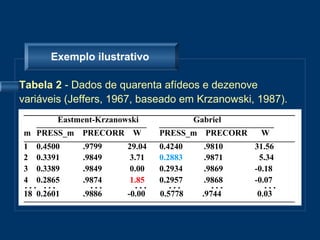
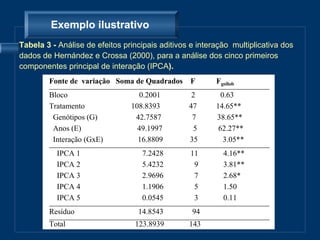
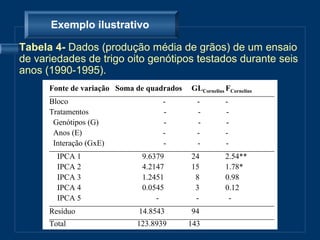
O documento descreve o modelo AMMI para análise de ensaios multiambientais, que modela efeitos principais e interação de forma sequencial. Dois métodos de validação cruzada são apresentados para otimizar a seleção do número de componentes multiplicativos no modelo AMMI: leave-one-out e uma mistura de regressão e aproximação de matrizes de posto inferior.