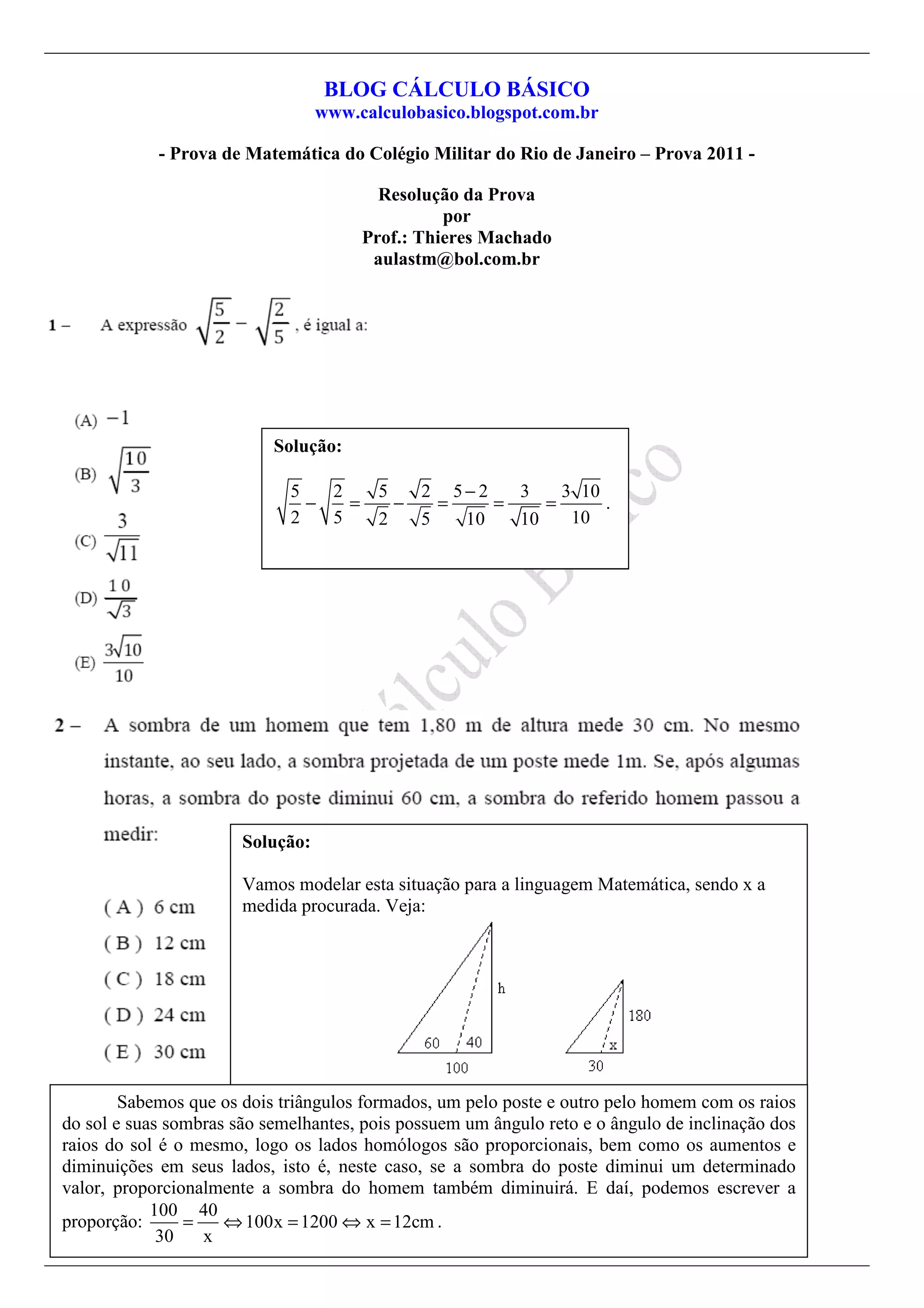
O documento apresenta uma série de resoluções de problemas matemáticos abordados em uma prova do Colégio Militar do Rio de Janeiro de 2011. As soluções utilizam conceitos de geometria, proporções e álgebra para resolver uma variedade de questões, incluindo triângulos, polígonos e distribuições de quantidades. O autor, prof. Thieres Machado, também oferece informações de contato para aulas particulares.

1. BLOG CÁLCULO BÁSICO
www.calculobasico.blogspot.com.br
- Prova de Matemática do Colégio Militar do Rio de Janeiro – Prova 2011 -
Resolução da Prova
por
Prof.: Thieres Machado
aulastm@bol.com.br
Solução:
5 2 5 2 5 2 3 3 10
2 5 102 5 10 10
−
− = − = = = .
Solução:
Vamos modelar esta situação para a linguagem Matemática, sendo x a
medida procurada. Veja:
Sabemos que os dois triângulos formados, um pelo poste e outro pelo homem com os raios
do sol e suas sombras são semelhantes, pois possuem um ângulo reto e o ângulo de inclinação dos
raios do sol é o mesmo, logo os lados homólogos são proporcionais, bem como os aumentos e
diminuições em seus lados, isto é, neste caso, se a sombra do poste diminui um determinado
valor, proporcionalmente a sombra do homem também diminuirá. E daí, podemos escrever a
proporção:
100 40
100x 1200 x 12cm
30 x
= ⇔ = ⇔ = .

2. Solução:
Para encontrarmos a medida do ângulo interno de um polígono regular,
usamos a relação
180.(n 2)
n
−
e para a medida do ângulo externo, também de
um polígono regular, usamos
360
n
, onde n representa o número de lados.
Portanto, do enunciado, temos:
180.(n 2)
n
−
-
360
n
= 144 180n 360 360 144n n 20⇔ − − = ⇔ = .
Solução:
Sejam a, b, c as medidas da hipotenusa e dos catetos, respectivamente. Do
enunciado temos:
a + b + c = 30 ( I )
a2
+ b2
+ c2
= 338 ( II )
b2
+ c2
= a2
( III ) Teorema de Pitágoras
Substituindo (III) em (II): 2 2
a a 338 a 13cm+ = ⇔ = . Substituindo o valor de
a = 13, em (III) e (I):
2 2
b c 169
b c 17
 + =

+ =
, fazendo a devida substituição, encontramos a equação na
incógnita c: 2 2
2c 34c 120 0 c 17c 60 0 c 12 ou c = 5− + = ⇔ − + = ⇔ = .
Para c = 12, b = 5 e para c = 5, b = 12. Portanto, o módulo da diferença será:
12 5 7cm ou 5 12 7cm− = − = .

3. Solução:
( )
( ) ( )
( )( )
( ) ( )
( )( )
( ) ( )
x x a a x ax a
x a x a2a 2ax a x a
x a x x a x x a a x a a x a x x a
a
x a x a x a x a x a x a
+ + −
+ − +− + + = + =
+ + − − − − +
− −
− + − − + −
( ) ( )
( ) ( )
( )
( ) ( )
( ) ( )
( ) ( )
( )
( ) ( )
( ) ( )
( ) ( )
( )
( ) ( )
( ) ( )
( ) ( )
x x a a x a 2a x a x x a a x a 2a x a
x x a a x a a x a x x a x x a a x a x x a a x a
x x a a x a 2a x a x x a a x a
1.
x x a a x a x x a a x a x x a a x a
+ + − − + + − −
= + = + =
+ − − − − + + − − − + − −  
+ + − − + − −
= − = =
+ − − + − − + − −
Solução:
3
2 2 2
3 3 6 8 6 8
11 1 2 2 4 2 3
8
2 5 33 5
8 84 4
2 35 3
1
ab6 6 8 24 248
3 3 4 12 12b
a
a b b a b a 1 1 1
a 1b a a b a b ab a ab
b ab a b ba a a b
b a ab b b a
1 1 1 1 1 1 1 1
a a b a b a b ab
− −
−− −
−
−
× ×
× = × = = =
= × = × = × = × = ⋅

4. Solução:
Lembrando que (a + b + c)2
= a2
+ b2
+ c2
+ 2( ab + ac + bc), vamos antes simplificar a
expressão dada.
(3a + b – 2c)2
– (2a – 3c)2
+ 5(c – a)(a + c) + b(2a – b) =
= 9a2
+ b2
+ 4c2
+ 2(3ab - 6ac – 2bc) – 4a2
+ 12ac – 9c2
+ 5c2
– 5a2
+ 2ab – b2
=
= 6ab – 12ac – 4bc + 12ac + 2ab = 8ab – 4bc a 7/18,b 5/8,c 2/9 7 5 5 2 25
8 4
18 8 8 9 18
= = =
→ ⋅ ⋅ − ⋅ ⋅ = ⋅
Solução:
Para obter a área do triângulo, precisamos antes saber sua dimensões, vamos então descobrir as
coordenadas do ponto c. Sabendo que f é uma função afim, sua lei é da forma: f(x) = ax + b ou y =
ax + b, com a, b∈ℝ e a 0≠ . Temos uma reta e b é a ordenada do ponto de interseção da reta com o
eixo vertical, isto é, o ponto de interseção da reta (gráfico de f) com o eixo vertical é c = (0,b) .
Utilizando os pontos (3,1) e (-2,-9) e y = ax + b:
resolvendo
3a b 1
a 2 e b = -5.
2a b 9
+ =
→ =
+ = −
Podemos escrever a lei da função f: f(x) = 2x - 5. Logo, c = (0,-5) e no triângulo retângulo ABC,
AB = 3, BC = 6.
Área de ABC = (3.6)/2 = 9 u.a.
(0,-5)

5. Prof. Thieres Machado
Professor de cursos preparatórios, com experiência em concursos públicos em geral.
Para aulas particulares ou em grupo envie um e-mail para:
aulastm@bol.com.br ou pelo tel.: (21) 9155-0291
BLOG CÁLCULO BÁSICO
Matemática para concursos
www.calculobasico.blogspot.com.br
Solução:
O que vem a ser capacidade, neste caso? Bem, capacidade é o quociente entre a quantidade de
envelopes distribuídos e o tempo gasto para distribuí-las.
Sendo C a capacidade total, Q quantidade total de envelopes e T o tempo total, temos C = Q/T.
Sejam CM, QM e TM as grandezas relacionadas a Marcelo e CJ, QJ e TJ as grandezas relacionadas a Jean.
Do enunciado, temos:
TJ = 110% do TM, então TJ = 1,1TM.
CM = 80% da CJ, então CM = 0,8CJ.
QM + QJ = 380, então QJ = 380 - QM.
J J MM
M J M
M J J
Q 0,8Q TQ
C 0,8C 0,8 Q
T T T
= → = ⋅ ⇔ = , agora fazendo as substituições em QJ e TJ, temos:
( )M MJ M
M M M M M
J M
0,8 380 Q T0,8Q T
Q Q 1,1Q 0,8Q 304 Q 160 cartas.
T 1,1T
−
= → = ⇔ + = ⇔ =
QJ = 380 - 160, então QJ = 220 envelopes.
Observando as alternativas, temos que a letra A é a correta, Jean distribui 220 envelopes.

6. Solução:
Como os retângulos são congruentes entre si, temos que todos possuem as mesmas dimensões. Seja x a
medida do comprimento e y a medida da largura de cada retângulo.
Na figura temos:
2x = 3y (relação entre as medidas do lados da figura).
4x + 5y = 176
3y
2.2x 5y 176 6y 5y 176 y 16cm, logo x = 24cm.
=
⇔ + = ⇔ + = ⇔ =
Área = 16.24 = 384 cm2
.
Solução:
Já sabemos encontrar a medida do ângulo interno de um polígono regular (veja questão/solução nº.3). O
ângulo interno (ai) do pentágono vale:
( )
i
180 5 2
a 108 .
5
−
= = ° Agora, veja a figura abaixo. No triângulo ADE, ˆˆADE DAE 36= = ° , pois o
triângulo ADE é isósceles com AE = DE. Portanto, o ângulo ˆBAD 108 36 72= °− ° = ° e sendo o ângulo
BÂD um ângulo de segmento, isto é, seu vértice está na circunferência e um de seus lados é tangente e o
outro secante à circunferência, sua medida é metade da medida do ângulo central correspondente. Sendo
AÔD o ângulo central, temos:
ˆAOD ˆ72 AOD 144 .
2
° = ⇔ = °
Seja x a medida do arco menor AD e por uma regra de três simples direta, pois o comprimento da
circunferência ( 2 rπ ) equivale a uma volta completa (360°), vamos determinar a medida procurada:
2 r 360 2 .5.144
x x 4 cm.
x 144 360
π π
π
− − − − ° °
→ = ⇔ =
− − − − ° °

7. Solução:
Sejam S, E e G o número de provas corrigidas pelos professores Sobral, Euler e Gil,
respectivamente. Do enunciado, temos:
E 60% de S, então E = 0,6.S.
G = 45% de E, então G = 0,45.E.
=
Das duas relações acima, podemos escrever uma terceira:
G 0,45.E 0,45.0,6.S, então G = 0,27.S.= =
Ainda, do enunciado:
S + E + G = 561 S 0,6S 0,27S 561 S 300.→ + + = ⇔ = Logo, E = 180 e G = 81.
Portanto, a resposta correta é a letra C, Gil corrigiu 81 provas.
Solução:
Em primeiro lugar, vamos verificar as restrições para esta equação.
x2
- 6x + 6 0≥ , fazendo x2
- 6x + 6 = 0 resolvendo
x 3 3→ = ± . Fazendo o estudo do sinal:
+ + + - - - - - - + + + temos que: x ;x 3 3 ou x 3+ 3∈ ≤ − ≥ℝ .
3 3− 3 3+
Agora, vamos resolver a equação dada fazendo uso de uma substituição, mas antes observe que:
2 2 2
x 6x 6 x 6x 9 6 9 x 6x 9 3.− + = − + + − = − + −
2 2 2 2
x 6x 9 4 x 6x 6 x 6x 9 4 x 6x 9 3− + = − + ⇔ − + = − + − . Fazendo x2
- 6x + 9 = y, vem:
( )
2
2 2
y 4 y 3 y 4 y 3 y 16y 48 0 y 12 ou y = 4.= − ⇔ = − ⇔ − + = ⇔ = Verificando:
para y = 12 12 4 12 3 (verdadeiro)→ = − e y = 4 4 4 4 3 (verdadeiro)→ = − . “Voltando”,
isto é, encontrando os valores das raízes em x:
Para y = 12, temos 2 2
x 6x 9 12 x 6x 3 0 x 3 3 (inteiros).− + = ⇔ − − = ⇔ = ± ∉ℤ
Para y = 4, temos 2
x 6x 5 0 x 5 ou x = 1.− + = ⇔ = Ambos os valores pertencem ao intervalo
verificado para a restrição.
Soma das raízes inteiras = 5 + 1 = 6.
Completando os quadrados

8. Solução:
Sejam x, y, z, w as quantias que os irmãos possuem no momento presente. Do
enunciado, temos:
x + y + z + w = 71 ( I )
x + 4 = y - 3 =
z
2
= 2w (valor final da importância de cada irmão), então
x = 2w - 4; y = 2w + 3 e z = 4w, agora, substituindo essas relações em ( I ),
vem que:
2w + 2w + 3 + 4w + w = 71 w 8⇔ = . Portanto, o valor final da importância
de cada um dos irmãos será: x + 4 = y - 3 =
z
2
= 2w = 2.8 = 16 reais.
Solução:
Sejam M, E e A a quantidade de oficiais presentes na reunião da Marinha, Exército e
Aeronáutica, respectivamente.
Do enunciado, temos que como saíram os oficiais da Aeronáutica, restam os oficiais da
Marinha e Exército (M + E):
M = 40% de (M + E), então M =
2
(M E)
5
+
3M
5M 2M 2E E
2
⇔ − = ⇔ = .
Do contrário, retiraram os oficiais da Marinha, restam os oficiais da Aeronáutica e Exército
(E + A):
E = 90% de (E + A), então E =
9
(E A)
10
+ , substituindo o valor de E encontrado acima:
E =
9
(E A)
10
+
:3
:3
3M 9 3M 30M 27M 18A A 3 1
A 3M 18A
2 10 2 20 20 M 18 6
+ 
→ = + ⇔ = ⇔ = ⇔ = = 
 
.

9. Solução:
Observe que: Área CDEF = Área ABCD - (Área ABE + Área FCB)
No triângulo ABE, por Pitágoras, temos que BE = 5 . Veja que AD é paralelo a BC e BE é transversal
aos lados AD e BC, portanto formam ângulos alternos internos, isto é, ˆ ˆAEB CBE≡ , além do mais,
ˆ ˆBAE BFC (retos)≡ , logo os triângulos ABE e FCB são semelhantes (possuem dois ângulos
correspondentes congruentes) e daí:
AE BE 1 5 2 5
BF
BF BC BF 2 5
= → = ⇔ = .
No triângulo FCB, por Pitágoras, temos que FC =
4 5
5
. Portanto, Área FCB =
2 5 4 5
45 5
2 5
×
= . Logo,
Área CDEF = 4 -
4 11
1
5 5
 
+ = 
 
cm2
.
Solução:
Sejam a, b algarismos e N um número inteiro. Temos, idade de Paulo = ab = 10a + b e
idade de Rebecca = ba = 10b + a.
Do enunciado:
(ab)2
- (ba)2
= N2
2 2
2 2 2 2 2
(ab ba).(ab ba) N (10a b 10b a).(10a b 10b a) N
(11a 11b).(9a 9b) N 11.9.(a b)(a b) N 9.11.(a b ) N
+ − = ⇔ + + + + − − = ⇔
⇔ + − = ⇔ + − = ⇔ − = ⇔
⇔ 32
.11.(a2
- b2
) = N2
.

10. Observação: No problema proposto acima, lembre-se que a, b são algarismos e podem assumir qualquer
valor, observando a restrições do enunciado, dos algarismos do sistema decimal, isto é, 0, 1, 2, 3, 4, 5, 6, 7, 8
ou 9 (no caso acima 5 e 6) e o quadrado de um número inteiro diferente de zero é sempre um número inteiro
positivo.
Observe que N2
é um quadrado perfeito, portanto os expoentes dos fatores primos devem ser pares.
Como temos dois fatores definidos (3 e 11) e o fator 3 tem expoente par, devemos voltar nossa atenção
para o fator 11, para que tenhamos expoente par para o fator 11, (a2
- b2
) deve ser igual a 11 ou uma
potência de base 11 com expoente ímpar, mas verifique que uma potência de base 11 e expoente maior
do que 1 não satisfará as alternativas ou/e o enunciado, portanto (a2
- b2
) = 11 e daí, podemos escrever:
(a2
- b2
) = 11 ( ) ( )a b . a b 11⇔ + − = , neste caso, a = 6 e b = 5. Assim, idade de Paulo = 65 anos e idade
de Rebecca = 56.
Soma das idades = 65 + 56 = 121.
Solução:
Preço (R$) Unidades Receita (R$)
150 270 40500
140 300 42000
130 330 42900
120 360 43200
110 390 42900
100 400 40000
. . .
. . .
. . .
Veja que, na tabela construída acima, a receita máxima é de R$ 43200, após a
receita tende a diminuir.

11. Prof. Thieres Machado
Professor de colégios, cursos preparatórios, com experiência em concursos públicos, militares, vestibulares,
escolas técnicas, reforço escolar, etc.
Para aulas particulares ou em grupo envie um e-mail para:
aulastm@bol.com.br ou pelo tel.: (21) 9155-0291
BLOG CÁLCULO BÁSICO
Matemática para concursos
www.calculobasico.blogspot.com.br
Solução:
1 1 1 1 1 1
1 . 1 . 1 . ... . 1 . 1 . ... . 1
2 3 4 2n 2n 1 200
3 2 5 4 2n 1 2n 199 198 201 201
2 3 4 5 2n 2n 1 198 199 200 200
           
+ − + + − + =           
+           
+
= ⋅ ⋅ ⋅ ⋅ ⋅⋅⋅ ⋅ ⋅ ⋅ ⋅⋅⋅ ⋅ ⋅ ⋅ = ⋅
+
Solução:
Seja x a medida do ângulo. Do enunciado, temos:
( )
( )
( )
( )
90 x
3. 180 2x 125 . Resolvendo esta equação:
4
90 x 90 x
3. 180 2x 125 540 6x 125 x 70 .
4 4
°−
° − + = °
°− °−
° − + = ° ⇔ ° − + = ° ⇔ = °
Dois ângulos são replementares quando sua soma é igual a 360°. Portanto, o
replemento de um ângulo x é: 360° - x.
Replemento de 70° = 360° - 70° = 290°.