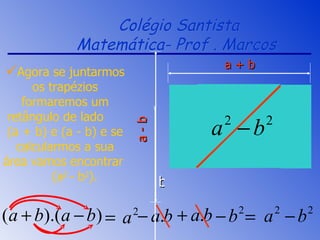
O documento apresenta os principais produtos notáveis e suas aplicações na fatoração de expressões algébricas. São descritos o quadrado da soma e da diferença de dois termos, a diferença de quadrados, o cubo da soma e da diferença de dois termos e exemplos de fatoração por fator comum e agrupamento.

1. Colégio Santista
Matemática- Prof . Marcos
7ª Série
Unidade Temática:
Produtos Notáveis
Fatoração

2. Colégio Santista
Matemática- Prof . Marcos
a b
Produtos Notáveis:
Quadrado a a 2
a.b
da Soma de
dois termos: b 2
a.b b
(a + b) = (a + b).(a + b)
2
Soma das Áreas= a + 2.a.b + b2 2

3. Colégio Santista
Matemática- Prof . Marcos
Produtos Notáveis: a
b
Quadrado da
diferença de dois
termos:
a
( a − b) 2
( a − b) 2
b

4. Colégio Santista
Matemática- Prof . Marcos
Produtos Notáveis:
a-b
Quadrado da
diferença de dois
termos.
Calculando a área
que sobrou teremos: a-b ( a − b) 2
(a − b) = (a − b).(a − b)
2
a − 2.a.b + b
2 2

5. Colégio Santista
Matemática- Prof . Marcos
Produtos Notáveis: a
Diferença de
quadrados:
2
a a
a −b
2 2
2 b
b
b

6. Colégio Santista
Matemática- Prof . Marcos
Após a subtração
da maior área pela
menor área,
marcamos com uma
diagonal separando
a área restante
dividindo-a em duas
partes, que são dois
trapézios.

7. Colégio Santista
Matemática- Prof . Marcos
a
Diferença de
quadrados:
Após separarmos a-b
as áreas, registramos
algebricamente as a
partes que sobraram
(lados do trapézio). b
b
a-b

8. Colégio Santista
Matemática- Prof . Marcos
a+b
Agora se juntarmos
os trapézios
formaremos um
retângulo de lado
a −b
2 2
a-b
(a + b) e (a - b) e se
calcularmos a sua
área vamos encontrar
(a2 - b2). b
(a + b).(a − b) = a − a.b + a.b − b = a − b
2 2 2 2

9. Colégio Santista
Matemática- Prof . Marcos
O Cubo da soma de
dois termos:
Considere um cubo de
aresta “a + b”, como b
o da figura ao lado.
O volume de um cubo
de arestas ℓ é ℓ3, a
então o volume do
cubo representado a
a b
pela figura é (a+b)3. b

10. Colégio Santista
Matemática- Prof . Marcos
Vamos separar as partes em que o cubo está dividido:
Um cubo de aresta “a”.
a Volume: a3.
a3
a
a

11. Colégio Santista
Matemática- Prof . Marcos
a
a a2b Três paralelepípedos
b que têm arestas
b a, a e b.
a Cada paralelepípedo
2b tem volume a2b.
a
a a2b O volume dos três
a paralelepípedos é
b 3a2b.
a

12. Colégio Santista
Matemática- Prof . Marcos
b
a Três paralelepípedos
b b que têm arestas
2
ab
a, b e b.
b ab2
b Cada paralelepípedo
a tem volume ab2.
ab2 O volume dos três
a
paralelepípedos é
b 3ab2.

13. Colégio Santista
Matemática- Prof . Marcos
b b
Um cubo de aresta “b”.
b b3 Volume: b3.

14. Colégio Santista
Matemática- Prof . Marcos
a2b
2
Somando todos esses
ab
ab2 b3 volumes temos:
b
a 3 2
a a + 3a b + 3ab + b
3 2 2 3
a2b ab2
Como o volume do todo é igual à
soma dos volumes das partes,
temos:
(a + b) = a + 3a b + 3ab + b
3 3 2 2 3

15. Colégio Santista
Matemática- Prof . Marcos
Esse mesmo resultado pode ser obtido através do
seguinte cálculo:
( a + b) = ( a + b) . ( a + b) =
3 2
Aplicando a propriedade distributiva:
= (a + b) . (a + 2ab + b ) =
2 2
a + 2 a b + ab + a b + 2ab + b
3 2 2 2 2 3

16. Colégio Santista
Matemática- Prof . Marcos
Portanto:
(a + b) = a + b + + b
3
3a 3
3ab 2 2 3
Cubo 2º Termo.
1º
3 x (1º termo) x (o quadrado do 2º termo).
Termo
3 x ( o quadrado do 1º termo) x (2º termo).
2º Termo
Cubo do 1º Termo.

17. Colégio Santista
Matemática- Prof . Marcos
O Cubo da diferença de dois termos:
Esse mesmo resultado pode ser obtido através do
seguinte cálculo:
( a − b) = ( a − b) . ( a − b) =
3 2
Aplicando a propriedade distributiva:
= (a − b) . (a − 2ab + b ) =
2 2
a − 2 a b + ab − a b + 2ab − b
3 2 2 2 2 3

18. Colégio Santista
Matemática- Prof . Marcos
Portanto:
(a − b) = a − b + − b
3
3a 3
3ab 2 2 3
Cubo 2º Termo.
1º
3 x (1º termo) x (o quadrado do 2º termo).
Termo
3 x ( o quadrado do 1º termo) x (2º termo).
2º Termo
Cubo do 1º Termo.

19. Colégio Santista
Matemática- Prof . Marcos
Hora da revisão:
Quadrado da soma de dois termos:
(a + b) = a + 2.a.b + b
2 2 2
Quadrado da diferença de dois termos:
(a − b) = a 2 − 2.a.b + b 2
2
Diferença de quadrados:
a − b = (a + b).(a − b)
2 2
Cubo da soma de dois termos:
(a + b) = a + 3a b + 3ab + b
3 3 2 2 3
Cubo da diferença de dois termos:
(a − b) = a − 3a b + 3ab − b
3 3 2 2 3

20. Colégio Santista
Matemática- Prof . Marcos
Fatoração:
x a
 Fator Comum
2
x x a.x
Calculando-se a
Área:
x.( x + a ) = x + a.x
2

21. Colégio Santista
Matemática- Prof . Marcos
a 4
Fatoração:
 Fator Comum
4.a a
Fazendo o fator
comum entre as 2a 2
2a
áreas
encontraremos :2a
Colocando o fator
em evidência
teremos:
2a.(a + 2) = 2.a + 4.a
2

22. Colégio Santista
Matemática- Prof . Marcos
Fatoração:  por agrupamento:
m n
a am an
b bm bn
(a + b).(m + n) = a.m + a.n + b.m + b.n

23. Colégio Santista
Matemática- Prof . Marcos
Fazendo o fator comum entre os
termos apresentados, volta-se ao início.
Aplicando o fator comum duplamente:
a.m + a.n + b.m + b.n = a.(m + n) + b.(m + n)
= (a + b).(m + n)