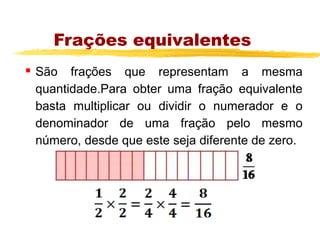
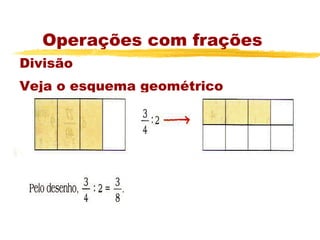
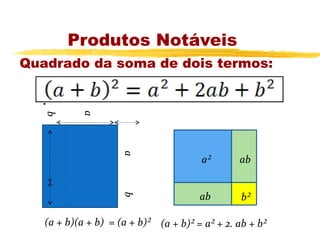
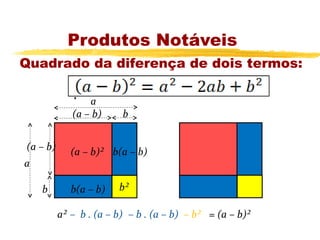
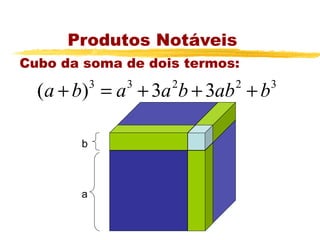
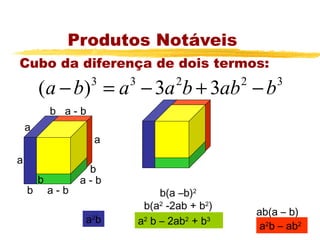
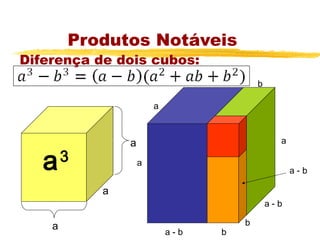
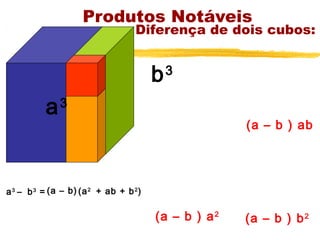
O documento apresenta os principais tópicos sobre operações com frações, incluindo frações equivalentes, adição, subtração, multiplicação e divisão de frações. Além disso, explica produtos notáveis como o quadrado da soma e da diferença de termos, cubo da soma e da diferença e a diferença e soma de cubos. A lista de exercícios contém questões sobre esses tópicos.

1. Operações com frações;
Produtos notáveis.
Abril de 2012
Matemática Básica
Prof. Benício França
josebeniciofranca@yahoo.com.br

2. Frações equivalentes
 São frações que representam a mesma
quantidade.Para obter uma fração equivalente
basta multiplicar ou dividir o numerador e o
denominador de uma fração pelo mesmo
número, desde que este seja diferente de zero.

3. Operações com frações
Adição e Subtração de frações
com mesmo denominador
 A soma de duas frações com mesmo
denominador é igual a uma nova fração cujo
denominador é o mesmo das frações dadas e o
numerador é a soma dos numeradores das
referidas frações. Para a subtração aplica-se a
mesma regra.

4. Operações com frações
Adição e Subtração de frações
com denominadores diferentes
 A soma ou a diferença de duas frações com
denominadores diferentes só é possível quando ambas
possuírem o mesmo denominador, para isso, basta
juntar as frações equivalentes às frações dadas no
mesmo denominador comum.

5. Operações com frações
Adição e Subtração de frações
com denominadores diferentes
Utilizamos o m.m.c. para obter as frações
equivalentes e depois somamos normalmente as
frações, que já terão o mesmo denominador.
Questão 1) da lista 1

6. Operações com frações
Multiplicação
Nas multiplicações de frações multiplica-se o numerador
com numerador e denominador com denominador. Se
necessário, simplifique o produto. A simplificação pode ser
antes ou após a multiplicação.
Veja os exemplos: Multiplica e depois simplifica

7. Operações com frações
Multiplicação
OU, simplifica e depois multiplica
 Questão 1) da lista 1

8. Operações com frações
Inverso de uma fração
 O inverso de uma fração é uma fração cujo
numerador é o denominador da fração dada e o
denominador é o numerador dela, ou seja, é só
inverter a posição do numerador e do denominador.
 Exemplo:

9. Operações com frações
Divisão

10. Operações com frações
Divisão
Veja o esquema geométrico

11. Operações com frações
Divisão
Na divisão de duas frações, multiplicamos a primeira fração
pelo inverso da segunda. Se necessário simplificamos.
 Questão 1) da lista.
Questão 2 da lista


12. Produtos Notáveis
Efetuar uma multiplicação é obter o produto.
Existem alguns produtos muito usuais. São eles:
Quadrado da soma de dois termos: (a + b)²
Quadrado da diferença de dois termos: (a - b)²
Produto da soma pela diferença de dois termos:
(a + b)(a – b)
Cubo da soma de dois termos: (a + b)³
Cubo da diferença de dois termos: (a – b)³
Diferença de dois cubos: a³ – b³
Soma de dois cubos: a³ + b³

13. Produtos Notáveis
Quadrado da soma de dois termos:
a
b
a
a² ab
ab b²
b
(a + b)(a + b) = (a + b)² (a + b)² = a² + 2. ab + b²

14. Produtos Notáveis
Quadrado da diferença de dois termos:
a
(a – b) b
(a – b) (a – b)² b(a – b)
a
b b(a – b) b²
a² – b . (a – b) – b . (a – b) – b² = (a – b)²

15. Produtos Notáveis
Produto da soma pela diferença de
dois termos:
(a + b) a
a b b
b
(a - b)
a a
b

16. Produtos Notáveis
Cubo da soma de dois termos:
(a + b) = a + 3a b + 3ab + b
3 3 2 2 3
b
a

17. Produtos Notáveis
Cubo da diferença de dois termos:
(a − b) = a − 3a b + 3ab − b
3 3 2 2 3
b a-b
a
a
a
b
b a-b
b a-b b(a –b)2
b(a2 -2ab + b2)
ab(a – b)
ab2
a2 b – 2ab2 + b3 a2b – ab2

18. Produtos Notáveis
Diferença de dois cubos:
b
a
a a
a 3 a
a-b
a
a-b
a b
a-b b

19. Produtos Notáveis
Diferença de dois cubos:
b3
a 3
(a – b ) ab
a 3 – b 3 = (a – b) (a 2 + ab + b 2 )
(a – b ) a 2 (a – b ) b 2

20. Produtos Notáveis
Cubo da Soma de dois termos:
 Lista de exercício questões 3, 4 e 5.