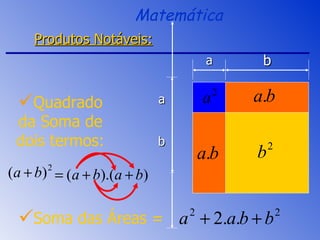
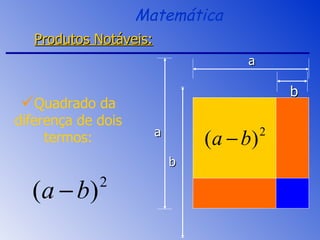
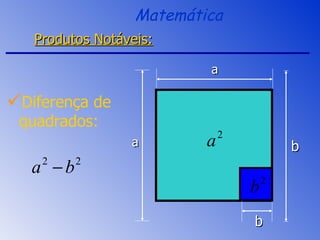
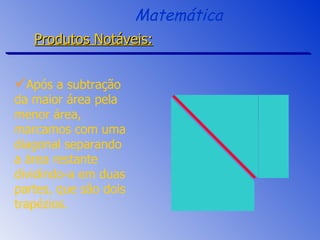
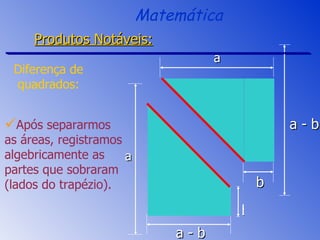
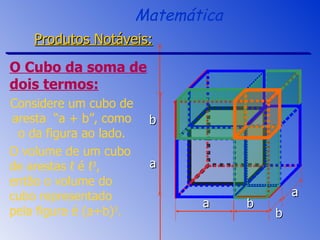
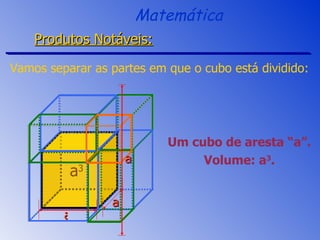
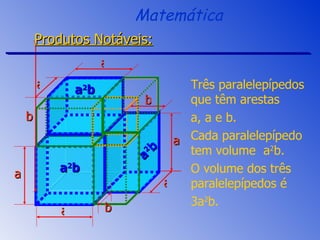
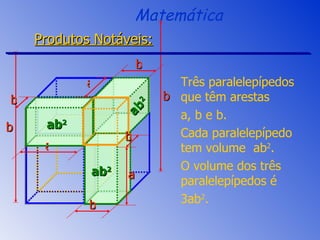
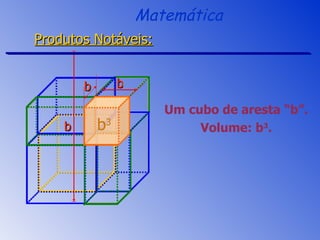
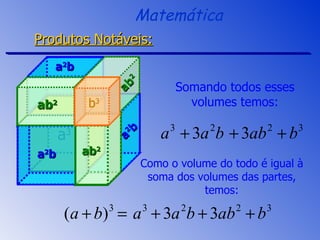
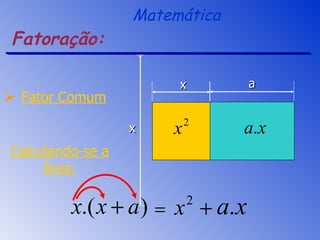
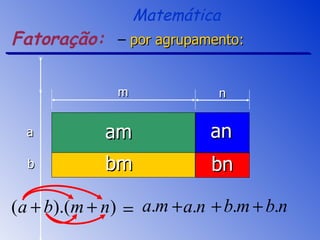
O documento aborda a fatoração e os produtos notáveis, incluindo o quadrado da soma, a diferença de quadrados e o cubo da soma e da diferença de dois termos. São apresentados os conceitos através de exemplos práticos e cálculos, focando nas áreas e volumes resultantes. A sessão de revisão destaca os principais tópicos e métodos de fatoração a serem aplicados.

1. Matemática Fatoração 7ª Série Unidade Temática: Produtos Notáveis

2. Matemática Produtos Notáveis: Quadrado da Soma de dois termos: Soma das Áreas = b a b a

3. Quadrado da diferença de dois termos: Matemática Produtos Notáveis: b a a b

4. Quadrado da diferença de dois termos. Calculando a área que sobrou teremos: Matemática Produtos Notáveis: a - b a - b

5. Diferença de quadrados: Matemática Produtos Notáveis: a a b b

6. Após a subtração da maior área pela menor área, marcamos com uma diagonal separando a área restante dividindo-a em duas partes, que são dois trapézios. Matemática Produtos Notáveis:

7. Após separarmos as áreas, registramos algebricamente as partes que sobraram (lados do trapézio). Diferença de quadrados: Matemática Produtos Notáveis: b a a b a - b a - b

8. Agora se juntarmos os trapézios formaremos um retângulo de lado (a + b) e (a - b) e se calcularmos a sua área vamos encontrar (a 2 - b 2 ). Matemática Produtos Notáveis: a + b a - b b

9. Considere um cubo de aresta “a + b”, como o da figura ao lado. O volume de um cubo de arestas ℓ é ℓ 3 , então o volume do cubo representado pela figura é (a+b) 3 . O Cubo da soma de dois termos: Matemática Produtos Notáveis: a b b a a b

10. Vamos separar as partes em que o cubo está dividido: Um cubo de aresta “a”. Volume: a 3 . a 3 Matemática Produtos Notáveis: a a a

11. Três paralelepípedos que têm arestas a, a e b. Cada paralelepípedo tem volume a 2 b. O volume dos três paralelepípedos é 3a 2 b. a 2 b a 2 b a 2 b Matemática Produtos Notáveis: b b a a a a b a a

12. Três paralelepípedos que têm arestas a, b e b. Cada paralelepípedo tem volume ab 2 . O volume dos três paralelepípedos é 3ab 2 . ab 2 ab 2 ab 2 Matemática Produtos Notáveis: b b a b a a b b b

13. Um cubo de aresta “b”. Volume: b 3 . b 3 Matemática Produtos Notáveis: b b b

14. Somando todos esses volumes temos: Como o volume do todo é igual à soma dos volumes das partes, temos: Matemática Produtos Notáveis: a 2 b a 2 b a 3 ab 2 a 2 b ab 2 ab 2 b 3

15. Esse mesmo resultado pode ser obtido através do seguinte cálculo: Aplicando a propriedade distributiva: Matemática Produtos Notáveis:

16. Portanto: 1º Termo 2º Termo Cubo do 1º Termo. Cubo 2º Termo. 3 x ( o quadrado do 1º termo) x (2 º termo). 3 x (1º termo) x ( o quadrado do 2 º termo). Matemática Produtos Notáveis:

17. Esse mesmo resultado pode ser obtido através do seguinte cálculo: Aplicando a propriedade distributiva: O Cubo da diferença de dois termos: Matemática Produtos Notáveis:

18. Portanto: 1º Termo 2º Termo Cubo do 1º Termo. Cubo 2º Termo. 3 x ( o quadrado do 1º termo) x (2 º termo). 3 x (1º termo) x ( o quadrado do 2 º termo). Matemática Produtos Notáveis:

19. Hora da revisão: Diferença de quadrados: Quadrado da soma de dois termos: Quadrado da diferença de dois termos: Cubo da soma de dois termos: Cubo da diferença de dois termos: Matemática Produtos Notáveis:

20. Fator Comum Fatoração: Calculando-se a Área: Matemática x a x

21. Fator Comum Colocando o fator em evidência teremos: Fazendo o fator comum entre as áreas encontraremos :2a Fatoração: Matemática 2a 4 a a

22. por agrupamento: am bm an bn Fatoração: Matemática b a m n

23. Fazendo o fator comum entre os termos apresentados, volta-se ao início. Aplicando o fator comum duplamente: por agrupamento: Fatoração: Matemática

24. Créditos Colégio Santista Matemática- Prof . Marcos Adaptado por Eliete Gomes Torquato Gonzaga