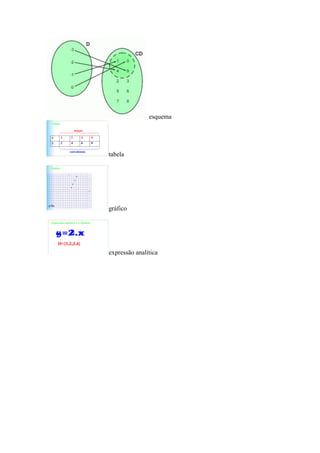
Uma função é uma relação entre dois conjuntos onde cada elemento do conjunto domínio é mapeado para um único elemento do conjunto contradomínio. Existem vários tipos de funções como funções lineares, trigonométricas, exponenciais e logarítmicas. Uma função é representada por seu domínio, contradomínio, conjunto imagem e pode ser mostrada por esquema, tabela, gráfico ou expressão analítica.

1. Jorge Cruz

2. O que é uma função?
Função é um dos conceitos mais importantes da matemática. Existem
várias definições, dependendo da forma como são escolhidos os axiomas.
Uma relação entre dois conjuntos, onde há uma relação entre cada um de
seus elementos. Também pode ser uma lei que para cada valor x é
correspondido por um elemento y, também denotado por f(x). Existem
inúmeros tipos de funções matemáticas, entre as principais temos: função
sobrejetora; função injetora; função bijetora; função trigonométrica;
Função linear; função modular; função do segundo grau; função
exponencial; função logarítmica; função Green; função polinomial; dentre
inúmeras outras. Cada função é definida por leis generalizadas e
propriedades específicas
Linguagem das funçoes
 Domínio: é o conjunto onde a função é definida [5], ou seja, ele
contém todos os elementos x para os quais a função deve ser
definida.
 Contradominio: é o conjunto que contém os elementos que podem
ser relacionados a elementos do domínio. Em outras palavras, é o
conjunto onde a função toma valores.[5] Dentro do contradomínio,
define-se o conjunto imagem como o conjunto de valores que
efetivamente f(x) assume.

3. Conjunto de chegada:
Imagens: é composto por todos os elementos em que as flechas de relacionamento
chegam.
Objeto:Uma vez que objectos são equivalentes a qualquer dado de outro tipo, é possível passar objectos como
agrupar de uma função. Objecto é são passados para função por valor , ou seja, uma cópia do objecto é feita
quando ele é passado para a função.
Modos de representação de uma função

4. esquema
tabela
gráfico
expressão analítica