O documento trata das medidas de posição em bioestatística, abordando a média, moda e mediana como medidas de tendência central e separatrizes. Detalha as propriedades relacionadas a cada uma dessas medidas, incluindo como calcular a média aritmética, encontrar a moda e determinar a mediana, tanto em conjuntos de dados simples quanto tabulados. Além de suas definições, o texto explica como cada medida pode ser afetada por operações matemáticas e valores extremos.

1. MEDIDAS DE POSIÇÃO
Profa
Ms Cristiane Leal M S Ferraz
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS
DEPARTAMENTO DE ENFERMAGEM, NUTRIÇÃO, FISIOTERAPIA E
GASTRONOMIA
CURSO: FISIOTERAPIA
DISCIPLINA: BIOESTATÍSTICA

2. MEDIDAS DE POSIÇÃO
A. Medidas de Tendência Central:
• Média
• Moda
• Mediana
B. Medidas Separatrizes:
• Mediana
• Quartis
• Decis
• Centis

3. MEDIDAS DE TENDÊNCIA CENTRAL
MÉDIA ARITMÉTCA: X
1. Média Aritmética Simples de um Rol:
X = ΣXi
n

4. MEDIDAS DE TENDÊNCIA CENTRAL
MÉDIA ARITMÉTCA: X
1. Média Aritmética Simples de um Rol
1. 1. Média Ponderada: para uma sequência numérica X1, X2, ...,
Xn afetados de pesos p1, p2, ... pn, respectivamente, a média
aritmética ponderada é definida por:
X = Σpi.Xi
Σpi

5. MEDIDAS DE TENDÊNCIA CENTRAL
MÉDIA ARITMÉTCA: X
2. Média Aritmética de Dados Tabulados:
X = Σfi.Xi
n

6. MEDIDAS DE TENDÊNCIA CENTRAL
MÉDIA ARITMÉTCA: X
3. Média Aritmética de Distribuição de Frequências:
X = Σfi.PM
n

7. MEDIDAS DE TENDÊNCIA CENTRAL
MÉDIA ARITMÉTCA: X
4. Propriedades da Média Aritmética:
4.1. Propriedade da Soma e da Subtração:
“Somando-se todos os elementos do conjunto com uma
constante, a média do novo conjunto será igual à média do
conjunto original também somada com aquela mesma
constante”.
• Serve para soma e para subtração.

8. MEDIDAS DE TENDÊNCIA CENTRAL
MÉDIA ARITMÉTCA: X
4. Propriedades da Média Aritmética:
4.1. Propriedade do Produto e Divisão:
“Multiplicando-se cada elemento de um conjunto original
por uma constante, a nova média será igual à média
anterior também multiplicada pela mesma constante”.
• Serve para produto e para divisão.

9. MEDIDAS DE TENDÊNCIA CENTRAL
MÉDIA ARITMÉTCA: X
4. Propriedades da Média Aritmética:
A MÉDIA É INFLUENCIADA PELAS QUATRO OPERAÇÕES

10. MEDIDAS DE TENDÊNCIA CENTRAL
MÉDIA ARITMÉTCA: X
4. Propriedades da Média Aritmética:
4.3. Outras Propriedade da Média Aritmética :
• A Média Aritmética sempre existe e é única
• A Média Aritmética é sensível a todos os valores do
conjunto. Se um valor se modifica, a média também se
modifica.
• A Média Aritmética é afetada por valores extremos.

11. MEDIDAS DE TENDÊNCIA CENTRAL
MÉDIA ARITMÉTCA: X
4. Propriedades da Média Aritmética:
4.4. Propriedade da Média das Médias Aritmética :
Trata-se de uma situação em que haverá alguns conjuntos
menores.
Xglobal = (nA.XA) + (nB.XB)
(nA + nB)

12. MEDIDAS DE TENDÊNCIA CENTRAL
MODA: Mo
 É aquele elemento que mais vezes aparece no conjunto, ou
seja, é o elemento que mais se repete.
 Trata-se de uma medida atípica (tanto pode não existir, como
ter uma ou várias Modas no conjunto).
1. Conjunto sem Moda: Amodal
2. Conjunto com uma única Moda: Unimodal
3. Conjunto com duas Modas: Bimodal
4. Conjunto com três ou mais Modas: Multimodal

13. MEDIDAS DE TENDÊNCIA CENTRAL
MODA: Mo
1. Moda para Rol:
A={1, 2, 2, 3, 3, 3, 4} Mo= 3
B={1, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5} Mo= 3, 5
C={1, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 6, 6, 7, 7, 7} Mo= 3, 5, 7
D={1, 2, 3, 4, 5} Mo= ?

14. MEDIDAS DE TENDÊNCIA CENTRAL
MODA: Mo
2. Moda para Dados Tabulados:
 Para determinarmos a Moda, basta procurar na coluna do fi
qual é a maior frequência absoluta simples.
Xi fi
1 3
2 7
3 10
4 15
5 3
6 2

15. MEDIDAS DE TENDÊNCIA CENTRAL
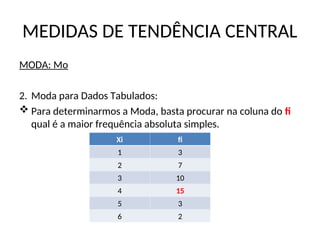
MODA: Mo
3. Moda para Distribuição de frequências:
 Passo inicial: achar a Classe Modal
Xi fi
(0; 10] 9
(10; 20] 15
(20; 30] 28
(30; 40] 17
(40; 50] 11
Maior fi: classe modal

16. h
p
a
a
l
Mo 













 inf
MEDIDAS DE TENDÊNCIA CENTRAL
MODA: Mo
3. Moda para Distribuição de frequências:
 Aplicação da fórmula:

17. MEDIDAS DE TENDÊNCIA CENTRAL
MODA: Mo
3. Moda para Distribuição de frequências:
 Aplicação da fórmula:
linf = limite inferior da classe modal.
a = diferença entre a fi da classe modal e a fi da classe
anterior.
p = diferença entre a fi da classe modal e a fi da classe
posterior.
h = amplitude da classe modal.

18. MEDIDAS DE TENDÊNCIA CENTRAL
MODA: Mo
4. Propriedades da Moda:
4.1. Propriedade da Soma e da Subtração:
“Somando-se todos os elementos do conjunto a uma mesma
constante, a nova moda será a anterior também somada
àquela constante”.
• Serve para soma e para subtração.

19. MEDIDAS DE TENDÊNCIA CENTRAL
MODA: Mo
4. Propriedades da Moda:
4.2. Propriedade do Produto e Divisão:
“Multiplicando todos os elementos de um conjunto original
por uma mesma constante, a nova moda será igual anterior
também multiplicada pela mesma constante”.
• Serve para produto e para divisão.

20. MEDIDAS DE TENDÊNCIA CENTRAL
MODA: Mo
4. Propriedades da Moda:
A MODA É INFLUENCIADA PELAS QUATRO OPERAÇÕES

21. MEDIDAS DE TENDÊNCIA CENTRAL
MODA: Mo
4. Propriedades da Moda:
4.3. Outras Propriedade da Moda :
• A Moda é uma medida atípica (pode não existir, ter uma ou
mais modas no conjunto)
• A Moda não é influenciada por valores extremos.

22. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
 É aquele elemento que separa o conjunto em duas partes
iguais, ou seja, em duas metades.
 Identificar a Md significa encontrar aquele elemento que está
exatamente no centro (no meio do conjunto), dividindo-o em
duas partes iguais (em duas metades).
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13}

23. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
1. Mediana para o Rol
 Procurar a Md de um rol é, na verdade, tentar identificar o
elemento que ocupa a Posição Central do conjunto.
Posição Central: {2, 5, 6, 11, 15}
Posição Central: {0, 1, 4, 5, 7, 12, 15, 18}

24. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
1. Mediana para o Rol
 Se o rol apresenta um número ímpar de elementos, existirá
apenas uma Posição Central.
 Se o rol apresenta um número par de elementos, existirão
duas Posições Centrais.

25. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
1. Mediana para o Rol com n Ímpar
{1, 1, 1, 3, 4, 5, 5, 7, 7, 8, 9, 9, 9, 9, 11, 13, 13, 15, 17, 18, 18}
n?
Par ou Ímpar?

26. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
1. Mediana para o Rol com n Ímpar
11ª posição
Md = 9
Posição Central = (n+1)
2

27. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
1. Mediana para o Rol com n Ímpar
 Quando o rol apresentar um número ímpar de elementos,
aquele elemento que ocupar a Posição Central será a própria
Mediana.
 Atenção! A mediana NÃO é a Posição Central, e sim o
elemento que a ocupa.

28. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
1. Mediana para o Rol com n Par
{1, 1, 1, 1, 3, 4, 5, 5, 7, 7, 8, 9, 9, 9, 9, 11, 13, 13, 15, 17, 18, 18}
n?
Par ou Ímpar?

29. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
1. Mediana para o Rol com n Par
11ª posição
12ª posição
1 ª Posição Central = n
2
2 ª Posição Central = a
que sucede a 1 ª

30. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
1. Mediana para o Rol com n Par
Md = 8,5
 A mediana de um conjunto não tem, necessariamente, que ser um de seus
elementos.
Md = 1ª PC + 2ª PC
2

31. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
2. Mediana para Dados Tabulados
par ou ímpar?
Posição Central: 25ª posição
Xi fi
2 5
4 10
6 15
8 11
10 5
12 3
n= 49

32. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
2. Mediana para Dados Tabulados
Xi fi fac
2 5 5
4 10 15
6 15 30
8 11 41
10 5 46
12 3 49
n= 49
“O valor desta fac é maior ou
igual ao valor da Posição
Central?”

33. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
2. Mediana para Dados Tabulados
Xi fi fac
2 5 5 Não
4 10 15 Não
6 15 30 SIM!
8 11 41
10 5 46
12 3 49
n= 49

34. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
2. Mediana para Dados Tabulados
Md = 6
Xi fi fac
2 5 5
4 10 15
6 15 30
8 11 41
10 5 46
12 3 49
n= 49

35. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
2. Mediana para Dados Tabulados
par ou ímpar?
1ª Posição Central: 25ª posição
2ª Posição Central: 26ª posição
Xi fi
2 5
4 10
6 15
8 11
10 6
12 3
n= 50

36. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
2. Mediana para Dados Tabulados
Xi fi fac
2 5 5
4 10 15
6 15 30
8 11 41
10 6 47
12 3 50
n= 50
“O valor desta fac é maior ou
igual ao valor da Posição
Central?”

37. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
2. Mediana para Dados Tabulados
1ª PC = 6
2ª PC = 6
Xi fi fac
2 5 5
4 10 15
6 15 30
8 11 41
10 6 46
12 3 49
n= 50

38. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
2. Mediana para Dados Tabulados
Md = 6
Md = 1ª PC + 2ª PC
2

39. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
3. Mediana para Distribuição de Frequências
 Passo 1: descobrir quem é a Classe Mediana do conjunto;
 Passo 2: aplicar a fórmula da Mediana para distribuição de
frequências.

40. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
3. Mediana para Distribuição de Frequências
 Determinação da Classe Mediana :
Passo 1: determinar valor de n.
Passo 2: calcular fração da mediana: (n/2)
“O valor desta fac é maior ou igual ao valor de (n/2)?”

41. MEDIDAS DE TENDÊNCIA CENTRAL
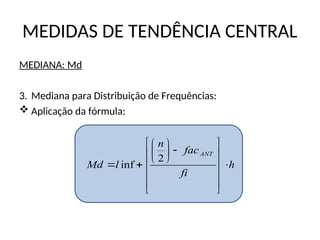
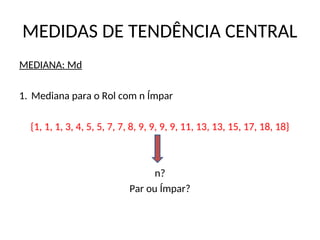
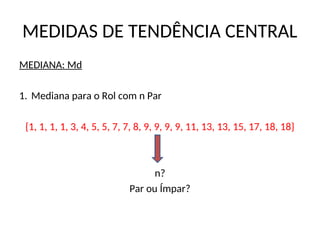
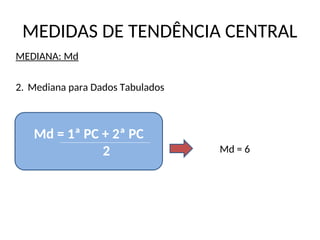
MEDIANA: Md
3. Mediana para Distribuição de Frequências
(n/2) = (20/2) = 10
Xi fi
(10; 20] 3
(20; 30] 5
(30; 40] 7
(40; 50] 4
(50; 60] 1
n= 20

42. MEDIDAS DE TENDÊNCIA CENTRAL
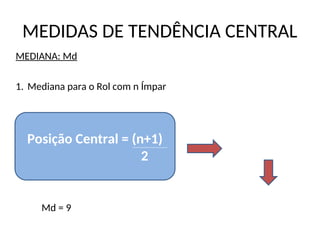
MEDIANA: Md
3. Mediana para Distribuição de Frequências
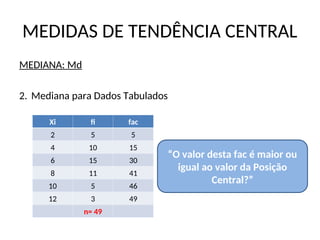
Xi fi fac
(10; 20] 3 3
(20; 30] 5 8
(30; 40] 7 15
(40; 50] 4 19
(50; 60] 1 20
n= 20
“O valor desta fac é maior ou
igual ao valor de (n/2)?”

43. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
3. Mediana para Distribuição de Frequências
Xi fi fac
(10; 20] 3 3 Não
(20; 30] 5 8 Não
(30; 40] 7 15 SIM!
(40; 50] 4 19
(50; 60] 1 20
n= 20

44. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
3. Mediana para Distribuição de Frequências
Xi fi fac
(10; 20] 3 3
(20; 30] 5 8
(30; 40] 7 15
(40; 50] 4 19
(50; 60] 1 20
n= 20

45. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
3. Mediana para Distribuição de Frequências:
 Aplicação da fórmula:
h
fi
fac
n
l
Md
ANT






















2
inf

46. MEDIDAS DE TENDÊNCIA CENTRAL
MEDIANA: Md
3. Mediana para Distribuição de Frequências:
 Aplicação da fórmula:
linf = limite inferior da classe mediana.
fac ANT= é a fac da classe anterior à classe mediana.
fi = é a frequência absoluta simples da classe mediana.
h = amplitude da classe mediana.