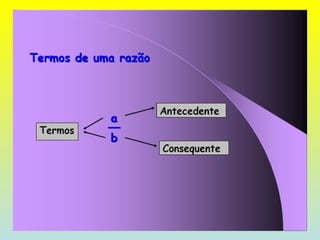
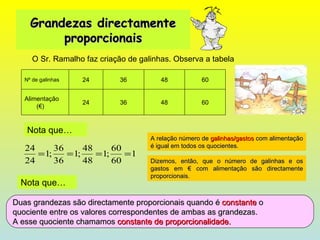
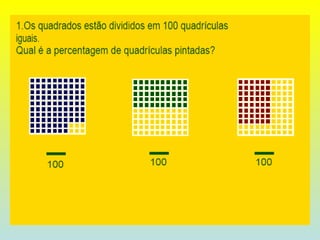
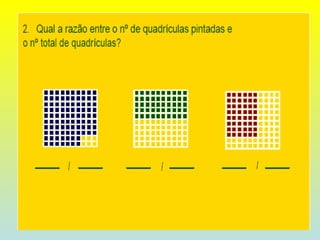
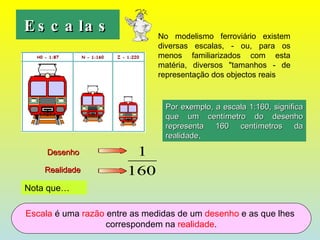
O documento discute razões, proporções e escalas. Explica que uma razão é a divisão entre duas grandezas e que uma proporção existe quando duas razões são iguais. Também define escala como a razão entre as medidas de um desenho e as correspondentes na realidade.

1. Vamos Estudar …

3. Razões Razão é uma relação entre os valores correspondentes de duas grandezas Nota que…

4. A palavra razão vem do latim ratio e significa a divisão ou o quociente entre dois números A e B, denotada por: ou A : B Exemplo : A razão entre 12 e 3 é 4 porque: Exemplo : A razão entre 3 e 6 é 0,5 porque:

5. Exemplo : Numa uma partida de basquete um jogador faz 20 arremessos e acerta 10 . Podemos avaliar o aproveitamento desse jogador, dividindo o número de arremessos que ele acertou pelo total de arremessos , o que significa que o jogador acertou 1 para cada dois arremessos, o que também pode ser pensado como o acerto de 0,5 para cada arremesso. 10 : 20 = 1 : 2 = 0,5 ou

6. Termos de uma razão Uma orquestra é formada por 40 homens e 30 mulheres. Qual a razão entre o número de homens e o número de mulheres? Qual a razão entre o número de mulheres e o número de homens? Numa razão é muito importante verificar a ordem pela qual estão referidas as duas grandezas Nota que… Uma razão tem dois termos , o antecedente e o consequente Na razão: antecedente consequente

7. Quando se escreve A > B ou A < B ou ainda A = B , estamos a comparar as grandezas A e B . Mas essa comparação, muitas vezes, pouco nos diz. Por isso, muitas vezes recorremos à razão entre duas grandezas, isto é, o quociente entre essas grandezas.

11. A bebida para a avó !!! Aplica

13. Como a avó gostava muito de café com leite , cada uma preparou em casa a bebida.

14. A Amélia utilizou 3 chávenas de café com 4 de leite.

15. A Carla utilizou 4 chávenas de café com 5 de leite.

16. A Jacinta misturou 5 chávenas de café com 6 chávenas de leite.

17. A avó gosta da bebida a saber a café .

18. Consegues descobrir qual das bebidas a avó gostou mais?

19. Na ilha de Spitzbergen, que se situa a 565 km a nordeste da costa da Noruega, em pleno Oceano Árctico, a razão entre o número de raposas polares e ursos polares é de 3 para 2. Supondo que nessa ilha existem 2000 animais destas duas espécies, quantos ursos e quantas raposas há na ilha? Podes utilizar palavras, esquemas ou cálculos para justificar a resposta. Exercício

21. Notas históricas: A palavra proporção vem do latim proportione e significa uma relação entre as partes de uma grandeza, ou seja, é uma igualdade entre duas razões . No século XV, o matemático árabe Al-Kassadi empregou o símbolo &quot;...&quot; para indicar as proporções e em 1.537, o italiano Niccola Fontana, conhecido por Tartaglia, escreveu uma proporção na forma 6:3::8:4.

22. Proporções - Introdução

23. Proporções O Filipe e o Cláudio decidiram ir dar uma volta com os seus cães. O Filipe pesa 30kg, e o seu cão, 10kg. O Cláudio , por sua vez, pesa 24kg, e seu cão, 8kg. Observa a razão entre o peso dos dois rapazes: Observa, agora, a razão entre o peso dos dois cães: Verificamos que as duas razões são iguais. Nesse caso, podemos afirmar que a igualdade é uma proporção . Assim: Nota que… Proporção é uma igualdade entre duas razões.

24. Grandezas directamente proporcionais O Sr. Ramalho faz criação de galinhas. Observa a tabela Nota que… A relação número de galinhas/gastos com alimentação é igual em todos os quocientes. Dizemos, então, que o número de galinhas e os gastos em € com alimentação são directamente proporcionais. Duas grandezas são directamente proporcionais quando é constante o quociente entre os valores correspondentes de ambas as grandezas. A esse quociente chamamos constante de proporcionalidade. Nota que… Nº de galinhas 24 36 48 60 Alimentação (€) 24 36 48 60

25. Dados quatro números racionais a, b, c, d, não-nulos, nessa ordem, dizemos que eles formam uma proporção quando a razão de a para b for igual à razão de c para d . Assim: Elementos de uma proporção ou a : b = c :d (lê-se “ a está para b assim como c está para d “ ) a, b, c e d são os termos da proporção, sendo: b e c os meios da proporção. a e d os extremos da proporção. Exemplo: Dada a proporção , temos: Leitura : 30 está para 24 assim como 10 está para 8 . Meios : 24 e 10 Extremos : 30 e 8

26. Observa as seguintes proporções: Produto dos extremos = 30x8 = 240 Produto dos meios = 24x10 = 240 Produto dos extremos = 12x5 = 60 Produto dos meios = 3x20 = 60 Temos que : Propriedade Fundamental das Proporções Daí podemos enunciar a propriedade fundamental das proporções: Em toda proporção, o produto dos meios é igual ao produto dos extremos. Nota que…

28. Exercícios de aplicação 1. Descobre o termo que falta em cada uma das proporções 5 x 20 = ? x 25 100 = ? X 25 ? = 100 : 25 ? = 4 2. A idade do Rui está para a da avó assim como 2 está para 9. O Rui tem 12 anos. Que idade tem a avó? 2 x ? = 9 x 12 2 x ? = 108 ? = 108 : 2 ? = 54 2 x ? = 3 x 6 2 x ? = 18 ? = 18 : 2 ? = 9

29. PERCENTAGENS

30. Um pouco da história das percentagens As percentagens já eram utilizadas pelos Babilónios. Este povo recorria às percentagens para os empréstimos. Pensa-se que o símbolo que actualmente utilizamos para designar percentagem - % - evoluiu do símbolo 0/0, este era utilizado no século XVII para juros, lucros... A palavra percentagem é derivada do latim per centum que significa &quot;de um cento&quot;. Uma percentagem pode ser apresentada sob a forma de razão ou sob a forma de numeral decimal . Por exemplo:

39. PERCENTAGENS Antes €84 Agora €42 Antes €90 Agora €81 Antes €80 Agora €60 Os pais do Rui inclinam-se para a compra do modelo que representa o desconto de 50%. Nota que… 50% significa a razão de cinquenta para cem , isto é, 50/100. Uma percentagem é uma razão em que o consequente é 100.

40. ESCALAS

41. Escala : Uma das aplicações da razão entre duas grandezas encontra-se na escala de redução ou escala de ampliação, conhecidas simplesmente como escala. Chamamos escala de um desenho à razão entre o comprimento considerado no desenho e o comprimento real correspondente, ambos medidos na mesma. Escala = A escala é a relação entre as distâncias representadas num mapa e as correspondentes distâncias reais. Como sabes, para representar a superfície da Terra no seu todo ou em parte numa folha de papel temos de reduzir a realidade. Por exemplo, se quiseres representar Portugal Continental numa folha de papel A4 tens de reduzir a dimensão do país cerca de 1,9 milhões de vezes.

42. Exemplo: O mapa do Brasil está em duas escalas diferentes.

43. Exemplo: Observemos as figuras dos barcos: O barco vermelho é uma ampliação do barco azul, pois as dimensões do barco vermelho são 2 vezes maiores do que as dimensões do barco azul , ou seja, os lados correspondentes foram reduzidos à metade na mesma proporção. Base menor barco azul / Base menor barco vermelho = 2/4 Base maior barco azul / Base maior barco vermelho = 4/8 Altura do barco azul / Altura do barco vermelho = 3/6

44. Escalas No modelismo ferroviário existem diversas escalas, - ou, para os menos familiarizados com esta matéria, diversos &quot;tamanhos - de representação dos objectos reais Por exemplo, a escala 1:160, significa que um centímetro do desenho representa 160 centímetros da realidade . Nota que… Escala é uma razão entre as medidas de um desenho e as que lhes correspondem na realidade . Desenho Realidade