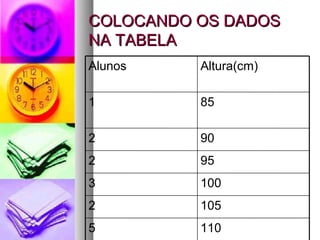
O documento explica conceitos estatísticos como média aritmética, desvio padrão, moda e mediana. A média aritmética de um conjunto de alturas de alunos é 101cm. A moda é 110cm, valor que mais aparece. Para calcular a mediana, os valores devem estar em ordem crescente e ela ocupa a posição central.

1. MedidasMedidas
MÉDIA ARITMÉTICA ;DESVIOMÉDIA ARITMÉTICA ;DESVIO
PADRÃO;MODA E MEDIANAPADRÃO;MODA E MEDIANA
Profª. Andréia

2. O QUE É MÉDIAO QUE É MÉDIA
ARITMÉTICA?ARITMÉTICA?
 média aritméticamédia aritmética de umde um
conjunto comconjunto com nn valores é avalores é a
soma desses valores divididossoma desses valores divididos
por n.por n.

3. VEJAMOS ESSE EXEMPLOVEJAMOS ESSE EXEMPLO
 No início do ano letivo, o professor deNo início do ano letivo, o professor de
Educação Física de uma escola mediu aEducação Física de uma escola mediu a
altura de todos as crianças de uma 4aaltura de todos as crianças de uma 4a
série para poder, ao final do ano letivo,série para poder, ao final do ano letivo,
comparar o desenvolvimento da turma. Nacomparar o desenvolvimento da turma. Na
pressa, ele anotou a altura das criançaspressa, ele anotou a altura das crianças
assim:assim:
 Maria, 1m; Selma, 95cm; Socorro,Maria, 1m; Selma, 95cm; Socorro,
1m10cm; Iracema, 90cm; Nilza, 1m; Elza,1m10cm; Iracema, 90cm; Nilza, 1m; Elza,
1m05cm; José, 85cm; Orestes, 95cm;1m05cm; José, 85cm; Orestes, 95cm;
Paulo, 1m; Ana, 1m10cm; Eliana, 1m10cm;Paulo, 1m; Ana, 1m10cm; Eliana, 1m10cm;
Sandra, 1m05cm; Renato, 1m10cm;Sandra, 1m05cm; Renato, 1m10cm;
Regina, 1m10cm; Marcelo, 90cm.Regina, 1m10cm; Marcelo, 90cm.

4. COLOCANDO OS DADOSCOLOCANDO OS DADOS
NA TABELANA TABELA
1105
1052
1003
952
902
851
Altura(cm)Alunos

5. Então teremos:Então teremos:
 Média 1 • (85) + 2Média 1 • (85) + 2.. (90) + 2 • (95)(90) + 2 • (95)
+ 3+ 3 .. (100) + 2 • (105) + 5(100) + 2 • (105) + 5 ..
(110)/15=101cm ou 1.01m(110)/15=101cm ou 1.01m

6. DESVIO PADRÃODESVIO PADRÃO
 É uma medida que ilustra quão próximos ouÉ uma medida que ilustra quão próximos ou
distantes da média estão os valores do conjuntodistantes da média estão os valores do conjunto
 COMO CALCULAR :COMO CALCULAR :
 1- subtraia da média obtida cada uma das alturas1- subtraia da média obtida cada uma das alturas
do conjunto de dadosdo conjunto de dados
 2- Eleve ao quadrado os valores encontrados2- Eleve ao quadrado os valores encontrados
 3- multiplique esses valores pela quantidade de3- multiplique esses valores pela quantidade de
elementos referentes a cada umelementos referentes a cada um
 4- Some todos os valores obtidos4- Some todos os valores obtidos
 5- divida o valor encontrado pela quantidade de5- divida o valor encontrado pela quantidade de
dados do conjuntodados do conjunto
 6-Extraia a raiz quadrada desse valor6-Extraia a raiz quadrada desse valor

7. MODAMODA
 A moda de um conjunto é oA moda de um conjunto é o
valor que mais aparece nessevalor que mais aparece nesse
conjunto.conjunto.

8. Moda = 110cm ou 1m10cmModa = 110cm ou 1m10cm
 Nessa situação, a altura maisNessa situação, a altura mais
frequente, ou a que mais ocorrefrequente, ou a que mais ocorre
(no caso, 5 crianças têm essa(no caso, 5 crianças têm essa
altura), é1m10cm, ou seja, modaaltura), é1m10cm, ou seja, moda
= 110cm.= 110cm.

9. MEDIANAMEDIANA
 Quando se tem uma quantidade ímpar deQuando se tem uma quantidade ímpar de
dados, a mediana é o valor que ocupa adados, a mediana é o valor que ocupa a
posição centralposição central
 EX: 1,2,3,4,5,6,7,8,9,EX: 1,2,3,4,5,6,7,8,9,
 Neste caso a mediana é o número 5Neste caso a mediana é o número 5
 Quando se tem um quantidade par deQuando se tem um quantidade par de
dados, a mediana é média aritmética dosdados, a mediana é média aritmética dos
dois valores centraisdois valores centrais
 EX: 1,2,3,4,5,6,7,8,9,10,11,12EX: 1,2,3,4,5,6,7,8,9,10,11,12
 Então temos:6+7/2=6.5Então temos:6+7/2=6.5
 Neste caso a mediana é 6.5Neste caso a mediana é 6.5
 A mediana de um conjunto é o valor queA mediana de um conjunto é o valor que
ocupa a posição central quando todos osocupa a posição central quando todos os
valores estão em ordem crescente.valores estão em ordem crescente.

10. MEDIANAMEDIANA
 Quando se tem uma quantidade ímpar deQuando se tem uma quantidade ímpar de
dados, a mediana é o valor que ocupa adados, a mediana é o valor que ocupa a
posição centralposição central
 EX: 1,2,3,4,5,6,7,8,9,EX: 1,2,3,4,5,6,7,8,9,
 Neste caso a mediana é o número 5Neste caso a mediana é o número 5
 Quando se tem um quantidade par deQuando se tem um quantidade par de
dados, a mediana é média aritmética dosdados, a mediana é média aritmética dos
dois valores centraisdois valores centrais
 EX: 1,2,3,4,5,6,7,8,9,10,11,12EX: 1,2,3,4,5,6,7,8,9,10,11,12
 Então temos:6+7/2=6.5Então temos:6+7/2=6.5
 Neste caso a mediana é 6.5Neste caso a mediana é 6.5
 A mediana de um conjunto é o valor queA mediana de um conjunto é o valor que
ocupa a posição central quando todos osocupa a posição central quando todos os
valores estão em ordem crescente.valores estão em ordem crescente.