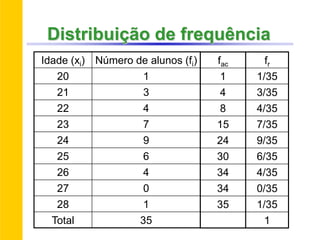
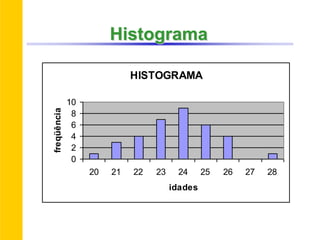
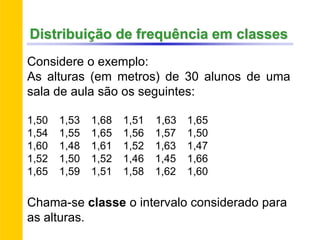
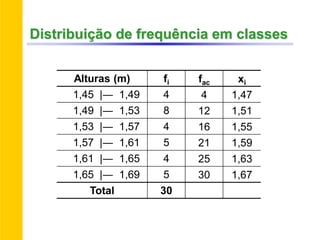
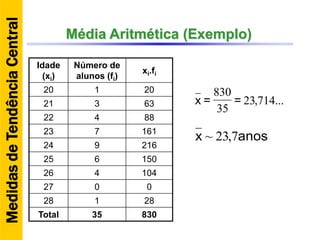
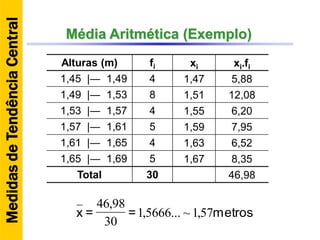
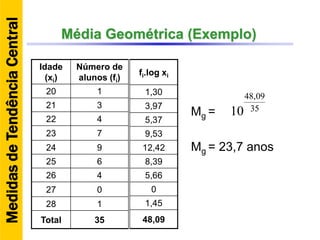
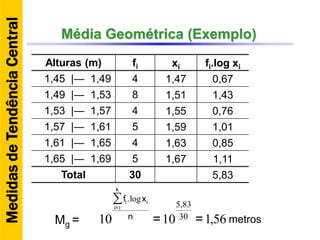
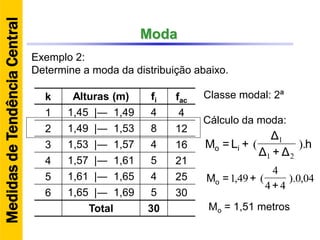
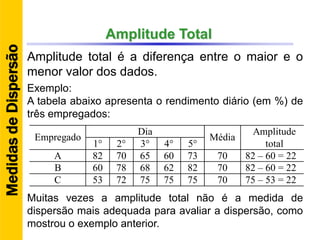
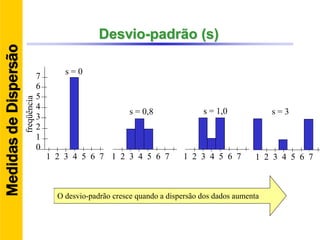
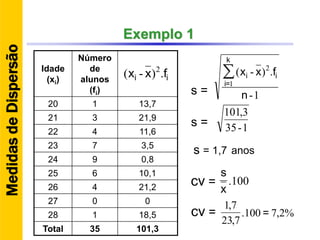
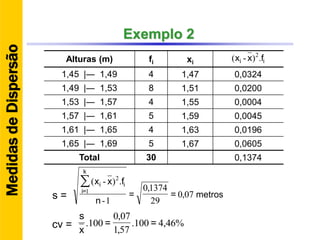
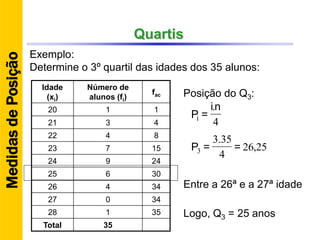
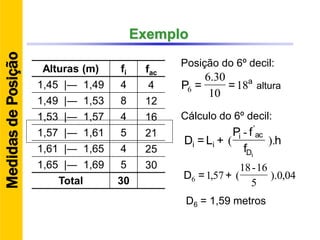
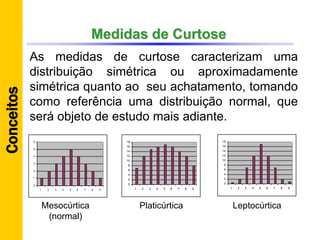
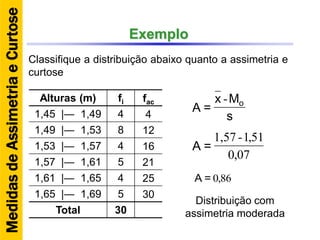
O documento discute conceitos básicos de estatística descritiva como distribuição de frequência, medidas de tendência central, histograma e moda. Explica como construir distribuições de frequência agrupando dados em classes e calcula exemplos de média aritmética, média geométrica, mediana e moda.

1. Probabilidade e Estatística
Prof. Dr.Narciso Gonçalves da Silva
http://paginapessoal.utfpr.edu.br/ngsilva
Estatística Descritiva

2. Distribuição de frequência
Para obter informações de interesse sobre
a característica em estudo, deve-se agrupar
os dados obtidos em uma distribuição de
frequência, onde os valores observados
não mais aparecerão individualmente.

3. Distribuição de frequência
Os dados abaixo representam as idades (em
anos) dos alunos de Estatística de um
determinado curso da UTFPR de Curitiba do
ano de 2010.
20 21 21 21 22 22 22
22 23 23 23 23 23 23
23 24 24 24 24 24 24
24 24 24 25 25 25 25
25 25 26 26 26 26 28
‘
RolCrescente

4. Distribuição de frequência
Idade (xi) Número de alunos (fi)
20 1
21 3
22 4
23 7
24 9
25 6
26 4
27 0
28 1
Total 35
fac
1
4
8
15
24
30
34
34
35
fr
1/35
3/35
4/35
7/35
9/35
6/35
4/35
0/35
1/35
1

5. Histograma
HISTOGRAMA
0
2
4
6
8
10
20 21 22 23 24 25 26 27 28
idades
freqüência

6. Distribuição de frequência em classes
Considere o exemplo:
As alturas (em metros) de 30 alunos de uma
sala de aula são os seguintes:
1,50 1,53 1,68 1,51 1,63 1,65
1,54 1,55 1,65 1,56 1,57 1,50
1,60 1,48 1,61 1,52 1,63 1,47
1,52 1,50 1,52 1,46 1,45 1,66
1,65 1,59 1,51 1,58 1,62 1,60
Chama-se classe o intervalo considerado para
as alturas.

7. Para se construir uma distribuição de freqüência
utilizando classes, deve-se determinar:
a) Número de classes (k):
Utiliza-se a Fórmula de Sturges:
k = 1 + 3,32.log n
onde: n = é o número de dados
e k deve ser um número inteiro positivo
b) Amplitude total dos dados (A):
A = Xmax – Xmin, onde Xmax é o valor máximo
da amostra e Xmin é o valor mínimo da amostra
Distribuição de frequência em classes

8. c) Intervalo de classe (h):
h = A/k
h deve ser um valor de modo que as classes
acomodem todos os dados da amostra
d) Limite inferior (Li) e Limite superior (Ls) da
classe:
Li é o menor valor dos dados da amostra
Ls = Li + h
Distribuição de frequência em classes

9. Distribuição de frequência em classes
Alturas (m) fi fac xi
1,45 |― 1,49 4 4 1,47
1,49 |― 1,53 8 12 1,51
1,53 |― 1,57 4 16 1,55
1,57 |― 1,61 5 21 1,59
1,61 |― 1,65 4 25 1,63
1,65 |― 1,69 5 30 1,67
Total 30

10. Medidas de Tendência Central
Medidas de tendência central são medidas
estatísticas, cujos valores estão próximos do
centro de um conjunto de dados dispostos
ordenadamente em rol crescente ou decrescente.
As mais conhecidas são:
• Média aritmética
• Média geométrica
• Média harmônica
• Mediana
• Moda
Conceitos

11. Média Aritmética
a) Dados brutos
A média aritmética de um conjunto de “n” valores
x1, x2, x3, ... ,xn é definida por:
n
x
n
xxxx
x
n
i
i
n



 1321 ...
Exemplo:
As idades (em anos) de 5 jogadores de futebol são: 18, 16,
15, 17, 17
A média aritmética das idades destes jogadores é:
6,16
5
171715161854321





n
xxxxx
x anos
MedidasdeTendênciaCentral

12. Média Aritmética
b) Dados agrupados
Se x1, x2, x3,...,xk ocorrem com as freqüências f1,
f2, f3, ... ,fk ,respectivamente, a média aritmética é
dada por:
n
fx
n
fxfxfxfx
x
k
i
ii
kk



 1332211
.
.......
Caso os dados sejam distribuídos em classes,
os valores x1, x2, x3,...,xk correspondem aos
pontos médios das “k” classes, ou seja:
2
si
i
LL
x


MedidasdeTendênciaCentral

13. Média Aritmética (Exemplo)
Idade
(xi)
Número de
alunos (fi)
xi.fi
20 1 20
21 3 63
22 4 88
23 7 161
24 9 216
25 6 150
26 4 104
27 0 0
28 1 28
Total 35 830
...714,23
35
830
==x
anosx 7,23~
MedidasdeTendênciaCentral

14. Média Aritmética (Exemplo)
Alturas (m) fi xi xi.fi
1,45 |― 1,49 4 1,47 5,88
1,49 |― 1,53 8 1,51 12,08
1,53 |― 1,57 4 1,55 6,20
1,57 |― 1,61 5 1,59 7,95
1,61 |― 1,65 4 1,63 6,52
1,65 |― 1,69 5 1,67 8,35
Total 30 46,98
metros==x 57,1~...5666,1
30
98,46
MedidasdeTendênciaCentral

15. Média Geométrica
a) Dados brutos
A média aritmética de um conjunto de “n” valores
x1, x2, x3, ... ,xn é definida por:
n
nxxxx .... 321  n
x
n
i
i
1
log
10Mg = =
Exemplo:
A média geométrica das idades dos 5 jogadores de futebol
do exemplo citado anteriormente é:
6,1617.17.15.16.185
Mg = anos
MedidasdeTendênciaCentral

16. Média Geométrica
b) Dados agrupados
Se x1, x2, x3,...,xk ocorrem com as freqüências f1,
f2, f3, ... ,fk ,respectivamente, a média geométrica é
dada por:
n f
k
fff k
xxxx .... 321
321 Mg = n
xf
k
i
ii
1
log.
10=
MedidasdeTendênciaCentral

17. Média Geométrica (Exemplo)
Idade
(xi)
Número de
alunos (fi)
20 1
21 3
22 4
23 7
24 9
25 6
26 4
27 0
28 1
Total 35
35
09,48
10Mg =
Mg = 23,7 anos
fi.log xi
1,30
3,97
5,37
9,53
12,42
8,39
5,66
0
1,45
48,09
MedidasdeTendênciaCentral

18. Média Geométrica (Exemplo)
Alturas (m) fi xi fi.log xi
1,45 |― 1,49 4 1,47 0,67
1,49 |― 1,53 8 1,51 1,43
1,53 |― 1,57 4 1,55 0,76
1,57 |― 1,61 5 1,59 1,01
1,61 |― 1,65 4 1,63 0,85
1,65 |― 1,69 5 1,67 1,11
Total 30 5,83
Mg = 56,11010 30
83,5
log.
1
==
∑
n
xf
k
=i
ii
metros
MedidasdeTendênciaCentral

19. Média Harmônica
a) Dados brutos
A média harmônica de um conjunto de “n” valores
x1, x2, x3, ... ,xn é definida por:
n
h
x
++
x
+
x
+
x
n
=M
1
...
111
321
Exemplo:
A média harmônica das idades dos 5 jogadores de futebol
do exemplo anterior é:
MedidasdeTendênciaCentral
54,16
17
1
17
1
15
1
16
1
18
1
5
=
++++
=Mh anos

20. Média Harmônica
b) Dados agrupados
Se x1, x2, x3,...,xk ocorrem com as freqüências f1,
f2, f3, ... ,fk ,respectivamente, a média aritmética é
dada por:
Caso os dados sejam distribuídos em classes,
os valores x1, x2, x3,...,xk correspondem aos
pontos médios das “k” classes.
MedidasdeTendênciaCentral
n
k
k
=i
i
h
x
f
++
x
f
+
x
f
+
x
f
f
=M
∑
...
3
3
2
2
1
1
1

21. Média Harmônica (Exemplo)
Alturas (m) fi xi fi/xi
1,45 |― 1,49 4 1,47 2,72
1,49 |― 1,53 8 1,51 5,30
1,53 |― 1,57 4 1,55 2,58
1,57 |― 1,61 5 1,59 3,14
1,61 |― 1,65 4 1,63 2,45
1,65 |― 1,69 5 1,67 2,99
Total 30 19,18
MedidasdeTendênciaCentral
56,1
18,19
30
...
3
3
2
2
1
1
1
==
x
f
++
x
f
+
x
f
+
x
f
f
=M
n
k
k
=i
i
h
∑
m

22. Mediana
a) Dados brutos
A mediana Me de um conjunto de “n” valores
ordenado x1, x2, x3,...,xn é representada pelo
valor central do conjunto para “n” ímpar e pela
média aritmética dos dois valores centrais para
“n” par.
Exemplos:
a) 3, 3, 4, 5, 7, 8, 9, 10, 12
Como n = 9, então, Me = 7
b) 3, 3, 4, 5, 7, 7, 9, 10
Como n = 8, então, Me = 6
2
75


MedidasdeTendênciaCentral

23. Mediana
a) Dados agrupados em intervalos de classes
Utiliza-se a expressão:
h
f
fP
LM
eM
ac
ie .
'







 

2
n
P Onde: é a posição da classe mediana
iL
acf '
eMf
h
é o limite inferior da classe mediana
é a frequência acumulada da classe
anterior à classe mediana
é frequência da classe mediana
é intervalo da classe mediana
MedidasdeTendênciaCentral

24. Mediana
Exemplo 1:
Determine a mediana da distribuição abaixo.
Idade
(xi)
Número de
alunos (fi)
fac
20 1 1
21 3 4
22 4 8
23 7 15
24 9 24
25 6 30
26 4 34
27 0 34
28 1 35
Total 35
Posição da mediana:
altura==P a
5,17
2
35
Me = 24 anos
Como n é ímpar, a
mediana é a 18ª idade
MedidasdeTendênciaCentral

25. Mediana
Exemplo 2:
Determine a mediana da distribuição abaixo.
Alturas (m) fi fac
1,45 |― 1,49 4 4
1,49 |― 1,53 8 12
1,53 |― 1,57 4 16
1,57 |― 1,61 5 21
1,61 |― 1,65 4 25
1,65 |― 1,69 5 30
Total 30
Posição da mediana:
h
f
fP
+L=M
eM
ac
ie ).
-
(
'
altura==P a
15
2
30
04,0).
4
12-15
(53,1 +=Me
Me = 1,56 metros
Cálculo da mediana:
MedidasdeTendênciaCentral

26. Moda
a) Dados brutos
A moda Mo de um conjunto de “n” valores x1,
x2, x3,...,xn é o número desse conjunto que
possuir a maior repetição. Se o conjunto não
tiver valores repetidos não existirá moda
(amodal) e se dois valores estiverem
igualmente repetidos, tem-se então duas
modas e o conjunto será dito bimodal.
A moda é o valor ao qual está associado a
freqüência mais alta.
MedidasdeTendênciaCentral

27. Moda
a) Dados agrupados em intervalos de classes
Fórmula de Czuber: hLM io .
21
1









iL
1
2
h
Onde:
é o limite inferior da classe modal. Chama-se classe
modal à classe de maior freqüência absoluta
é a diferença entre a freqüência da classe modal e
a freqüência da classe imediatamente anterior
é a diferença entre a freqüência da classe modal e a
freqüência da classe imediatamente posterior
é o intervalo da classe modal.
MedidasdeTendênciaCentral

28. Moda
Exemplo 1:
Determine a moda da distribuição abaixo.
Idade
(xi)
Número de
alunos (fi)
20 1
21 3
22 4
23 7
24 9
25 6
26 4
27 0
28 1
Total 35
Moda é a idade que mais
se repete, ou seja, a que
tem maior frequência.
Logo, Mo = 24 anos.
MedidasdeTendênciaCentral

29. Moda
Exemplo 2:
Determine a moda da distribuição abaixo.
k Alturas (m) fi fac
1 1,45 |― 1,49 4 4
2 1,49 |― 1,53 8 12
3 1,53 |― 1,57 4 16
4 1,57 |― 1,61 5 21
5 1,61 |― 1,65 4 25
6 1,65 |― 1,69 5 30
Total 30
Classe modal: 2ª
h
Δ+Δ
Δ
+L=M io ).(
21
1
04,0).
44
4
(49,1
+
+=Mo
Mo = 1,51 metros
Cálculo da moda:
MedidasdeTendênciaCentral

30. Medidas de Dispersão
As medidas de tendência central, por si só, não
são suficientes para caracterizar duas
distribuições estatísticas.
Exemplo:
Dois candidatos à emprego fizeram 5 provas e
vamos comparar seus rendimentos com base na
media aritmética.
Candidato A: 70, 71, 69, 70, 70 Média = 70
Candidato B: 40, 80, 98, 62, 70 Média = 70
Com base somente na média aritmética diríamos
que os dois candidatos apresentaram o mesmo
rendimento. Porém, como podemos observar o
candidato A apresentou notas mais uniformes.
Conceitos

31. Medidas de Dispersão
Para avaliar quantitativamente o grau de
variabilidade ou dispersão dos valores de um
conjunto de números em torno do valor médio,
utiliza-se ferramentas estatísticas denominadas
medidas de dispersão.
As principais medidas são:
• Amplitude total
• Desvio médio
• Variância
• Desvio-padrão
• Coeficiente de variação
Conceitos

32. Amplitude Total
Dia Amplitude
Empregado
1° 2° 3° 4° 5°
Média
total
A 82 70 65 60 73 70 82 – 60 = 22
B 60 78 68 62 82 70 82 – 60 = 22
C 53 72 75 75 75 70 75 – 53 = 22
Exemplo:
A tabela abaixo apresenta o rendimento diário (em %) de
três empregados:
Amplitude total é a diferença entre o maior e o
menor valor dos dados.
Muitas vezes a amplitude total não é a medida de
dispersão mais adequada para avaliar a dispersão, como
mostrou o exemplo anterior.
MedidasdeDispersão

33. Desvio Médio (d)
O desvio médio de um conjunto de “n” valores
x1, x2, x3, ... , xn é dada pela expressão:
n
xx∑
n
=i
i
1
-
d =
Para dados agrupados:
n
xxf∑
k
=i
ii
1
-
d =
Esta medida de dispersão considera todos os
valores do conjunto de dados.
MedidasdeDispersão

34. Variância Amostral (s2)
1-
)-(
1
2
n
xx∑
n
=i
i
A variância de um conjunto de “n” valores x1, x2,
x3, ... , xn é a média aritmética dos quadrados
do desvio médio de cada valor se estes dados
são de uma população.
s2 =
1-
.)-(
1
2
n
fxx∑
k
=i
ii
Para dados agrupados: s2 =
MedidasdeDispersão
Se os dados são de uma amostra, a variância é
dada pela expressão:

35. Desvio-padrão (s)
Desvio-padrão é a raiz quadrada da variância,
ou seja:
1-
)-(
1
2
n
xx∑
n
=i
i
s =
1-
.)-(
1
2
n
fxx∑
k
=i
ii
s =
para dados brutos
para dados agrupados
MedidasdeDispersão

36. Desvio-padrão (s)
s = 3
1 2 3 4 5 6 7
s = 1,0
1 2 3 4 5 6 7
s = 0,8
1 2 3 4 5 6 71 2 3 4 5 6 7
s = 0
7
6
5
4
3
2
1
0
O desvio-padrão cresce quando a dispersão dos dados aumenta
MedidasdeDispersão

37. Coeficiente de Variação (CV)
Coeficiente de variação é a razão entre o
desvio-padrão e a média aritmética, em
porcentagem, ou seja:
100.
x
s
cv =
MedidasdeDispersão

38. Exemplo 1
Idade
(xi)
Número
de
alunos
(fi)
20 1 13,7
21 3 21,9
22 4 11,6
23 7 3,5
24 9 0,8
25 6 10,1
26 4 21,2
27 0 0
28 1 18,5
Total 35 101,3
ii fxx .)-( 2
1-
.)-(
1
2
n
fxx∑
k
=i
ii
s =
1-35
3,101
s =
s = 1,7 anos
100.
x
s
cv =
%2,7100.
7,23
7,1
=cv =
MedidasdeDispersão

39. Exemplo 2
Alturas (m) fi xi
1,45 |― 1,49 4 1,47 0,0324
1,49 |― 1,53 8 1,51 0,0200
1,53 |― 1,57 4 1,55 0,0004
1,57 |― 1,61 5 1,59 0,0045
1,61 |― 1,65 4 1,63 0,0196
1,65 |― 1,69 5 1,67 0,0605
Total 30 0,1374
ii fxx .)-( 2
07,0
29
1374,0
1-
.)-(
1
2
==
n
fxx∑
k
=i
ii
%46,4100.
57,1
07,0
100. ==
x
s
cv =
s = metros
MedidasdeDispersão

40. Medidas de Posição ou Separatrizes
São medidas que dividem um conjunto de
valores em um certo número de partes iguais. A
mediana, por exemplo, divide um conjunto de
dados em duas partes iguais.
Conceitos
As outras principais medidas de posição são:
• Quartis
• Decis
• Centis ou Percentis

41. Quartis
O quartil divide um conjunto de valores ordenado em
quatro partes iguais. O primeiro quartil (Q1) é o valor
que antecede 25% da freqüência abaixo dele e
sucede 75%, segundo quartil (Q2) é igual ao valor da
mediana e terceiro quartil (Q3) é o valor que antecede
75% da freqüência abaixo dele e sucede 25%.
A expressão para cálculo do quartil “i” é a mesma da
mediana:
h
f
fP
+L=Q
IQ
aci
ii ).
-
(
'
4
.ni
=PiOnde a posição do quartil “i” é dada por:
MedidasdePosição
com i = 1, 2, 3

42. Quartis
Idade
(xi)
Número de
alunos (fi)
fac
20 1 1
21 3 4
22 4 8
23 7 15
24 9 24
25 6 30
26 4 34
27 0 34
28 1 35
Total 35
4
.ni
=Pi
Exemplo:
Determine o 3º quartil das idades dos 35 alunos:
Posição do Q3:
25,26
4
35.3
3 ==P
Entre a 26ª e a 27ª idade
Logo, Q3 = 25 anos
MedidasdePosição

43. Decis
O decil divide um conjunto de valores
ordenados em dez partes iguais e são
representados por D1, D2, ... , D9. O 5º decil é a
mediana.
A expressão para calcular o decil “i” é:
h
f
fP
+L=D
ID
aci
ii ).
-
(
'
10
.ni
=PiOnde a posição do decil “i” é dada por:
MedidasdePosição
com i = 1, 2, ... , 9

44. Centis ou Percentis
O centil divide um conjunto de valores
ordenados em 100 partes iguais e são
representados por C1, C2, ... ,C99. O 50º centil é
a mediana e o 25º e 75º centis correspondem
ao 1º e ao 3º quartis, respectivamente.
A expressão para calcular o centil “i” é:
h
f
fP
+L=C
IC
aci
ii ).
-
(
'
100
.ni
=PiOnde a posição do centil “i” é dada por:
MedidasdePosição
com i = 1, 2, 3, ... , 99

45. Exemplo
Alturas (m) fi fac
1,45 |― 1,49 4 4
1,49 |― 1,53 8 12
1,53 |― 1,57 4 16
1,57 |― 1,61 5 21
1,61 |― 1,65 4 25
1,65 |― 1,69 5 30
Total 30
No exemplo das alturas dos 30 alunos determine o 3º
quartil, 6º decil e 20º centil.
Posição do 3º quartil:
h
f
fP
+L=Q
IQ
aci
ii ).
-
(
'
a
==P 5,22
4
30.3
3
04,0).
4
12-5,22
(61,13 +=Q
Q3 = 1,63 metros
Cálculo do 3º quartil:
MedidasdePosição
Interpretação: 75% dos alunos têm
altura menor ou igual a 1,63 m e 25%
das alturas são superiores a 1,63 m

46. Exemplo
Alturas (m) fi fac
1,45 |― 1,49 4 4
1,49 |― 1,53 8 12
1,53 |― 1,57 4 16
1,57 |― 1,61 5 21
1,61 |― 1,65 4 25
1,65 |― 1,69 5 30
Total 30
Posição do 6º decil:
h
f
fP
+L=D
ID
aci
ii ).
-
(
'
a
==P 18
10
30.6
6
04,0).
5
61-81
(57,16 +=D
D6 = 1,59 metros
Cálculo do 6º decil:
altura
MedidasdePosição

47. Exemplo
Alturas (m) fi fac
1,45 |― 1,49 4 4
1,49 |― 1,53 8 12
1,53 |― 1,57 4 16
1,57 |― 1,61 5 21
1,61 |― 1,65 4 25
1,65 |― 1,69 5 30
Total 30
Posição do 20º centil:
h
f
fP
+L=C
IC
aci
ii ).
-
(
'
a
==P 6
100
30.20
20
04,0).
8
4-6
(49,120 +=C
C20 = 1,50 metros
Cálculo do 20º centil:
altura
MedidasdePosição

48. Medidas de Assimetria
As medidas de assimetria procuram
caracterizar o quanto o histograma de uma
distribuição de freqüência se afasta da
condição de simetria em relação à uma medida
de tendência central.
0
2
4
6
8
10
1 2 3 4 5 6 7 8 9
0
2
4
6
8
10
1 2 3 4 5 6 7 8 9
Distribuição assimétrica
positiva
Distribuição assimétrica
negativa
Conceitos

49. Coeficiente de Assimetria de Pearson (A)
s
Mx
=A o-
A
A
O grau de assimetria de uma distribuição de
frequência pode ser avaliada utilizando o
coeficiente de Pearson:
• < 0,15 : distribuição praticamente simétricaA
• 0,15 < < 1 : distribuição assimétrica moderada
• > 1 : distribuição fortemente assimétrica
MedidasdeAssimetria

50. Medidas de Curtose
As medidas de curtose caracterizam uma
distribuição simétrica ou aproximadamente
simétrica quanto ao seu achatamento, tomando
como referência uma distribuição normal, que
será objeto de estudo mais adiante.
0
1
2
3
4
5
6
1 2 3 4 5 6 7 8 9
0
2
4
6
8
10
12
14
16
18
1 2 3 4 5 6 7 8 9
0
2
4
6
8
10
12
14
16
18
1 2 3 4 5 6 7 8 9
Mesocúrtica
(normal)
Platicúrtica Leptocúrtica
Conceitos

51. Coeficiente Percentílico de Curtose (C)
)-(2
-
1090
2575
CC
CC
=C
O grau de achatamento com relação a
distribuição normal de uma distribuição de
frequência pode ser avaliado através do
coeficiente percentílico:
• Se C = 0,263: distribuição é mesocúrtica (normal)
• Se C < 0,263: distribuição leptocúrtica (alongada)
• Se C > 0,263: distribuição platicúrtica (achatada)
Onde C10, C25, C75 e C90 são os 10º, 25º, 75º e
90º centis (ou percentis)
MedidasdeCurtose

52. Exemplo
Alturas (m) fi fac
1,45 |― 1,49 4 4
1,49 |― 1,53 8 12
1,53 |― 1,57 4 16
1,57 |― 1,61 5 21
1,61 |― 1,65 4 25
1,65 |― 1,69 5 30
Total 30
Classifique a distribuição abaixo quanto a assimetria e
curtose
07,0
51,1-1,57
=A
s
Mx
=A o-
86,0=A
Distribuição com
assimetria moderada
MedidasdeAssimetriaeCurtose

53. Exemplo
Alturas (m) fi fac
1,45 |― 1,49 4 4
1,49 |― 1,53 8 12
1,53 |― 1,57 4 16
1,57 |― 1,61 5 21
1,61 |― 1,65 4 25
1,65 |― 1,69 5 30
Total 30
Logo, a distribuição é
platicúrtica
48,104,0).
4
0-3
(45,110 =+=C
51,104,0).
8
4-7,5
(49,125 =+=C
63,104,0).
4
21-22,5
(61,175 =+=C
263,0316,0
)48,1-67,1.(2
1,51-1,63
>==C
67,104,0).
5
25-27
(65,190 =+=C
MedidasdeAssimetriaeCurtose