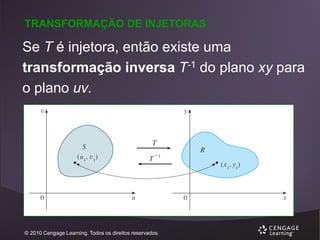
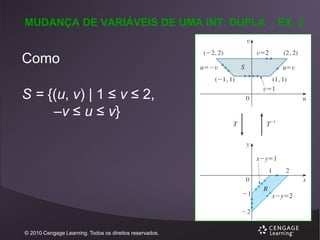
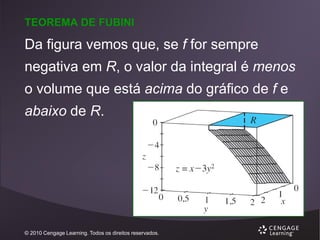
O documento discute integrais múltiplas. Ele introduz o conceito de integrais iteradas e como expressar integrais duplas como integrais iteradas, permitindo que sejam calculadas como integrais unidimensionais. O documento também apresenta o Teorema de Fubini, que estabelece que a ordem da integração em integrais duplas não importa, e fornece exemplos para ilustrar esses conceitos.




![INTRODUÇÃO
Suponha que f seja uma função de duas
variáveis contínua no retângulo
R = [a, b] x [c, d].
Usaremos a notação
d
c
f ( x, y) dy
significando que x é mantido fixo e f (x, y) é
integrada em relação a y de y = c até y = d.
© 2010 Cengage Learning. Todos os direitos reservados.](https://image.slidesharecdn.com/integraismultiplas-131107135731-phpapp01/85/Integrais-multiplas-5-320.jpg)

























![INTEGRAIS ITERADAS
Calcule
onde
R = [1, 2] x [0, ]
© 2010 Cengage Learning. Todos os direitos reservados.
EXEMPLO 3](https://image.slidesharecdn.com/integraismultiplas-131107135731-phpapp01/85/Integrais-multiplas-33-320.jpg)








![INTEGRAIS ITERADAS
EXEMPLO 4
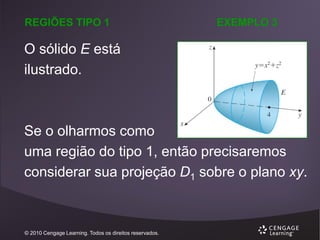
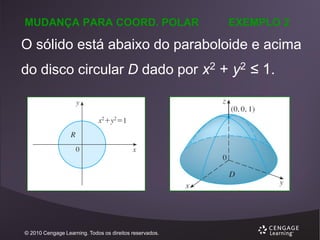
Observemos primeiro que S é o sólido que está
abaixo da superfície z = 16 – x2 – 2y2
acima do quadrado R = [0, 2] x [0, 2].
© 2010 Cengage Learning. Todos os direitos reservados.](https://image.slidesharecdn.com/integraismultiplas-131107135731-phpapp01/85/Integrais-multiplas-42-320.jpg)



![INTEGRAIS ITERADAS
Para sermos específicos, suponha que:
f(x, y) = g(x)h(y)
R = [a, b] x [c, d]
© 2010 Cengage Learning. Todos os direitos reservados.](https://image.slidesharecdn.com/integraismultiplas-131107135731-phpapp01/85/Integrais-multiplas-46-320.jpg)


![INTEGRAIS ITERADAS
Equação 5
Portanto, nesse caso, a integral dupla de f
pode ser escrita como o produto de duas
integrais unidimensionais:
g ( x)h( y ) dA g ( x) dx h( y ) dy
b
d
a
c
R
onde R = [a, b] x [c, d]
© 2010 Cengage Learning. Todos os direitos reservados.](https://image.slidesharecdn.com/integraismultiplas-131107135731-phpapp01/85/Integrais-multiplas-49-320.jpg)
![INTEGRAIS ITERADAS
Equação 5
Se R = [0, /2] x [0, /2], então, pela
Equação 5,
© 2010 Cengage Learning. Todos os direitos reservados.](https://image.slidesharecdn.com/integraismultiplas-131107135731-phpapp01/85/Integrais-multiplas-50-320.jpg)













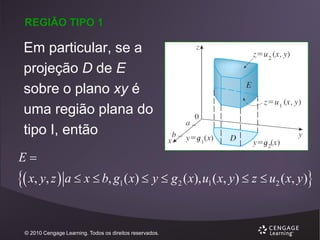
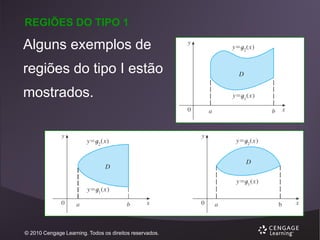
![REGIÕES DO TIPO 1
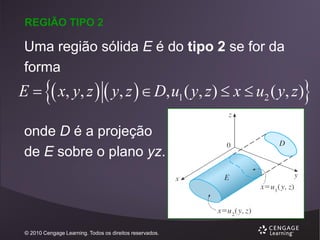
Uma região plana D é dita do tipo I se for a
região entre o gráfico de duas funções
contínuas de x, ou seja,
D = {(x, y) | a ≤ x ≤ b, g1(x) ≤ y ≤ g2(x)}
onde g1 e g2 são contínuas em [a, b].
© 2010 Cengage Learning. Todos os direitos reservados.](https://image.slidesharecdn.com/integraismultiplas-131107135731-phpapp01/85/Integrais-multiplas-64-320.jpg)
![REGIÕES DO TIPO 1
Para calcular
f ( x, y) dA quando D é do
D
tipo I, escolhemos um retângulo
R = [a, b] x [c, d] que contenha D e
consideramos a
função F definida
na Equação 1;
© 2010 Cengage Learning. Todos os direitos reservados.](https://image.slidesharecdn.com/integraismultiplas-131107135731-phpapp01/85/Integrais-multiplas-66-320.jpg)







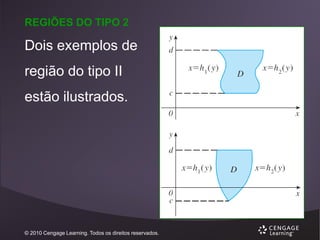


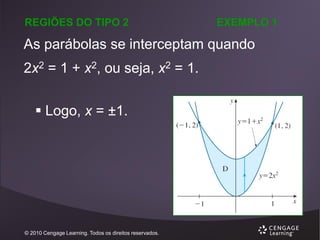
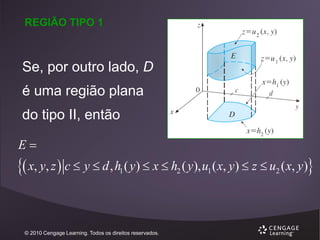
![REGIÕES DO TIPO 2
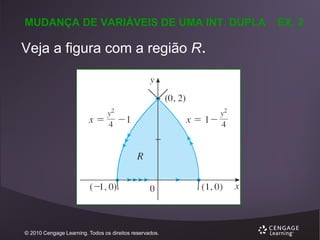
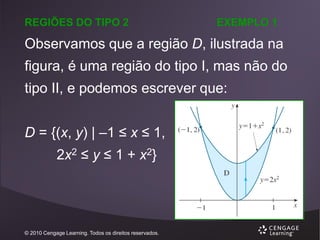
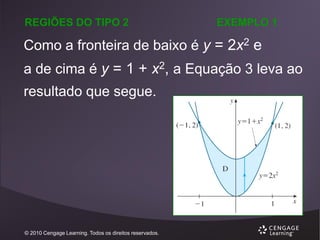
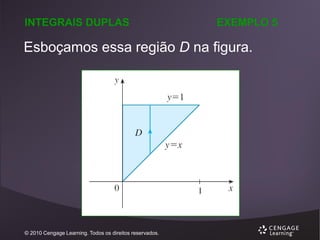
EXEMPLO 1
( x 2 y) dA
D
1
1 x 2
1 2 x
2
( x 2 y ) dy dx
[ xy y ]
1
2 y 1 x 2
y 2 x2
1
dx
[ x(1 x 2 ) (1 x 2 ) 2 x(2 x 2 ) (2 x 2 ) 2 ] dx
1
1
(3 x 4 x3 2 x 2 x 1) dx
1
1
1
x x
x x
32
3 2 x
5 4
3 2
1 15
5
4
3
2
© 2010 Cengage Learning. Todos os direitos reservados.](https://image.slidesharecdn.com/integraismultiplas-131107135731-phpapp01/85/Integrais-multiplas-80-320.jpg)








































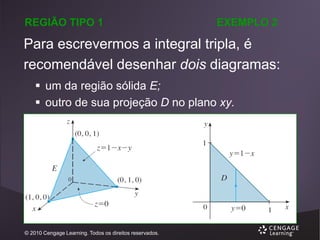
![INTEGRAIS TRIPLAS
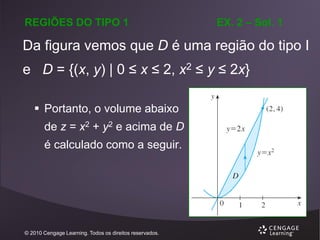
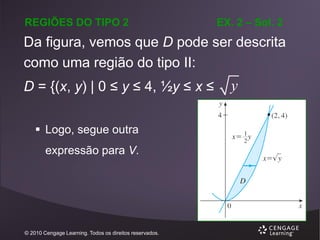
O primeiro passo é
dividir B em
subcaixas.
Fazemos isso dividindo:
o intervalo [a, b] em l subintervalos [xi-1, xi] de
comprimentos iguais Δx.
[c, d] em m subintervalos de comprimentos Δy.
[r, s] em n subintervalos de comprimento Δz.
© 2010 Cengage Learning. Todos os direitos reservados.](https://image.slidesharecdn.com/integraismultiplas-131107135731-phpapp01/85/Integrais-multiplas-124-320.jpg)






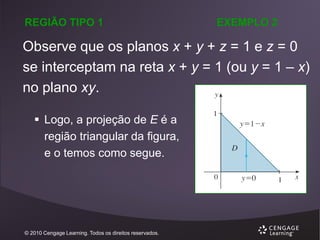
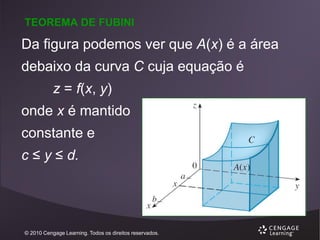
![TEOREMA DE FUBINI (INTEGRAIS TRIPLAS)
Se f é contínua em uma caixa retangular
B = [a, b] x [c, d] x [r, s], então
f x, y, z dV
B
s
r
f x, y, z dx dy dz
d
b
c
a
© 2010 Cengage Learning. Todos os direitos reservados.
T. 4](https://image.slidesharecdn.com/integraismultiplas-131107135731-phpapp01/85/Integrais-multiplas-131-320.jpg)