O documento aborda o cálculo de integrais múltiplas, focando na integral dupla, sua definição, interpretação geométrica e propriedades. Apresenta o teorema de Fubini e exemplos práticos para calcular volumes e áreas utilizando integrais duplas em regiões específicas. O material também discute a linearidade, monotonicidade e aditividade da integral dupla, além de explicar o método das somas de Riemann para aproximação do volume sob a superfície.



![Aula 1: Integrais Múltiplas
CÁLCULO IV
Integral Definida
Definição:
Seja f uma função definida ao menos no intervalo
fechado [a,b]. Então a área com sinal sob o gráfico
de f entre x=a e x=b é denotada por
( )
b
a
f x dx
Portanto, podemos escrever,
b
a
b
f
a
f
dx
x
f )
(
)
(
)
(](https://image.slidesharecdn.com/aula01-240823002915-81e194eb/85/Aula-de-Matematica-Integrais-Multiplas-ppt-4-320.jpg)

![Aula 1: Integrais Múltiplas
CÁLCULO IV
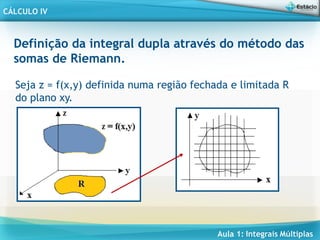
Interpretação Geométrica da Integral Dupla
Considere uma função real z = f(x,y) definida e contínua no
retângulo R = [a,b] x [c,d].
O retângulo R pode ser escrito como:
R = { (x,y) 2
| a ≤ x ≤ b e c ≤ y ≤ d }
Ambas as notações podem ser usadas, pois estão
descrevendo a mesma região.](https://image.slidesharecdn.com/aula01-240823002915-81e194eb/85/Aula-de-Matematica-Integrais-Multiplas-ppt-6-320.jpg)
![Aula 1: Integrais Múltiplas
CÁLCULO IV
Integral definida →
Área da função y = f(x) no intervalo [a,b] e geometricamente
seria descrita por:
b
a
A
A
dx
x
f 2
1
)
(](https://image.slidesharecdn.com/aula01-240823002915-81e194eb/85/Aula-de-Matematica-Integrais-Multiplas-ppt-7-320.jpg)

![Aula 1: Integrais Múltiplas
CÁLCULO IV
Exemplo
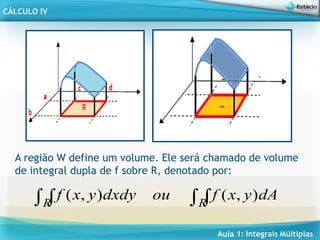
Se f(x,y) = 1 - x e R = [0,1] x [0,1].
A região R será definida pelos pontos:
f(x,y) no ponto x = 0, y = 0 será f(x,y) = 1. Então teremos
o ponto (0,0,1).
f(x,y) no ponto x = 0, y = 1 será f(x,y) = 0. Então teremos
o ponto (0,1,0).
f(x,y) no ponto x = 1, y = 0 será f(x,y) = 0. Então teremos
o ponto (1,0,0).
f(x,y) no ponto x = 1, y = 1 será f(x,y) = 0. Então teremos
o ponto (1,1,0).](https://image.slidesharecdn.com/aula01-240823002915-81e194eb/85/Aula-de-Matematica-Integrais-Multiplas-ppt-10-320.jpg)
![Aula 1: Integrais Múltiplas
CÁLCULO IV
Cálculo da Integral Dupla
Resolvendo a primeira integral dupla
Seja f(x,y) = 1 – x e R = [0,1] x [0,1].
1
0
1
0
)
1
(
)
,
( dxdy
x
dxdy
y
x
f
b
a
d
c](https://image.slidesharecdn.com/aula01-240823002915-81e194eb/85/Aula-de-Matematica-Integrais-Multiplas-ppt-12-320.jpg)



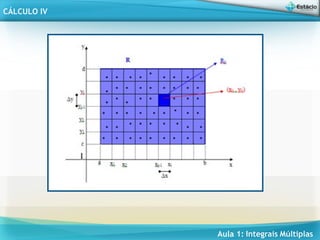
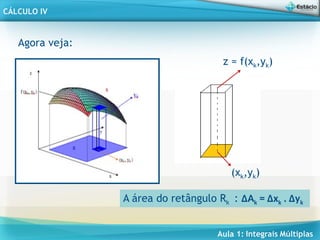








![Aula 1: Integrais Múltiplas
CÁLCULO IV
Teorema de Fubine
Se z = f(x,y) é contínua no retângulo R = [a,b] x [c,d],
então a integral dupla de f sobre R pode ser obtida
através de integrais iteradas, ou seja:
d
c
b
a
b
a
d
c
R
dy
dx
y
x
f
dx
dy
y
x
f
dA
y
x
f )
,
(
)
,
(
)
,
(
O Teorema de Fubine é prático para o cálculo de integrais
duplas através de duas integrações sucessivas de funções de
uma variável.](https://image.slidesharecdn.com/aula01-240823002915-81e194eb/85/Aula-de-Matematica-Integrais-Multiplas-ppt-27-320.jpg)
![Aula 1: Integrais Múltiplas
CÁLCULO IV
Exemplo
Seja f(x,y) em R = [-1,1] x [0, π/2].
Podemos escrever:
1
1
2
0
2
0
1
1
)
,
(
)
,
(
dydx
y
x
f
dxdy
y
x
f](https://image.slidesharecdn.com/aula01-240823002915-81e194eb/85/Aula-de-Matematica-Integrais-Multiplas-ppt-28-320.jpg)