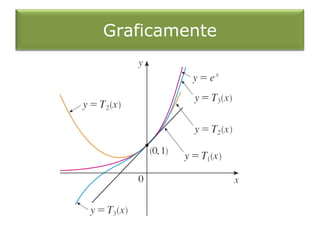
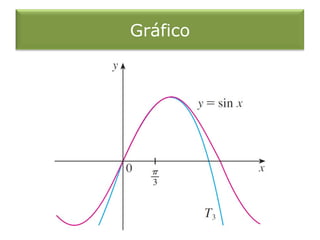
O documento discute séries de Taylor e de Maclaurin. Apresenta a fórmula para os coeficientes das séries e exemplos de como encontrar as séries de funções como exponencial, seno, cosseno e outras. Explica as condições para uma função ser igual à soma de sua série de Taylor.

1. Prof. Roberto Cristóvão
robertocristovao@gmail.com
Aula 18
Séries de Taylor e de Maclaurin

2. Série de Taylor e de Maclaurin
Se tiver uma representação (expansão)
em série de potências em isto é, se
então seus coeficientes são dados pela
fórmula

3. Série de Taylor
Substituindo essa fórmula para de volta
na série, então teremos a chamada série
de Taylor da função em (ou em
torno de ou centrada em )

4. Série de Maclaurin
Para o caso especial , a série de
Taylor torna-se
e recebe o nome especial de série de
Maclaurin

5. Exemplo 1
Encontre a série de Maclaurin da função
e seu raio de convergência.
Solução: Se então
Assim para todo
Logo a série de Maclaurin é

6. Exemplo 1
Fazendo temos
Pelo Teste da Razão a série converge para
todo , e o raio de convegência é

7. Investigação
Sob quais circunstâncias uma função é igual
à soma de sua série Taylor?
Em outras palavras, se tiver derivadas de
todas as ordens, quando é verdade que

8. Polinômio de Taylor de grau n
é o limite da sequência das somas
parciais. No caso da série de Taylor, as
somas parciais são:
é chamado polinômio de Taylor de
grau de em

9. Ilustração
Para os polinômios de Taylor em
0 com e 3 são

10. Teste de Comparação no LimiteGraficamente

11. Teorema
Se , onde é um
polinômio de Taylor de grau de em
e
para , então é igual à soma
de uma série de Taylor no intervalo

12. Exemplo 3
Encontre a série de Taylor de em
Solução:

13. Exemplo 4
Encontre a série de Maclaurin para senx.
Solução:

14. Exemplo 5
Encontre a série de Maclaurin para cosx.
Solução:

15. Exemplo 6
Encontre a série de Maclaurin para xcosx.
Solução:

16. Exemplo 7
Represente f (x)=senx como a soma de sua
série de Taylor centrada em π/3.
Solução:

17. Exemplo 7
Represente f (x)=senx como a soma de sua
série de Taylor centrada em π/3.
Solução:

18. Exemplo 7

19. Gráfico

20. Exemplo 8
Encontre a série de Maclaurin para
onde é um número real.
Solução:

21. Exemplo 8
(Série Binomial)
Converge se .
Notação radicional:

22. Série Binomial
Se é um número real e , então

23. Exemplo 9
Encontre a série de Maclaurin para afunção
e seu raio de convergência.

24. Solução
Série binomial com . Substituindo por :

25. Solução
A série converge para , ou seja, .
Portanto o raio de convergência é

26. Tabela

27. Exemplo 10
Calcule com erro inferior a 0,001.
Solução:

28. Exemplo