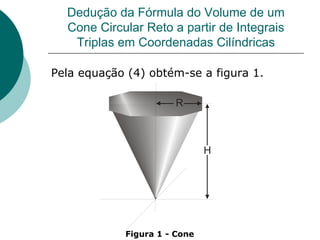
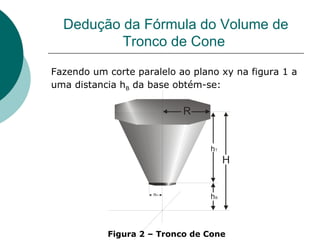
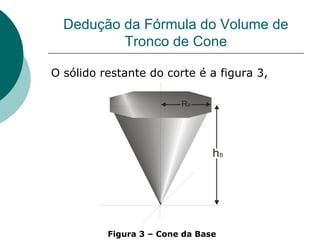
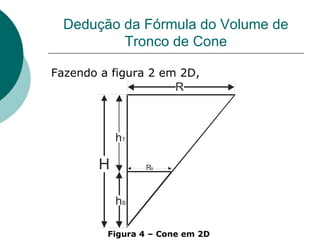
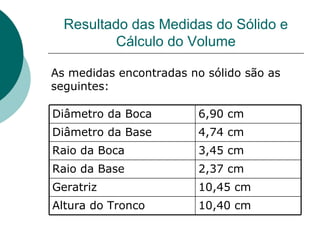
Este documento apresenta a dedução da fórmula do volume de um cone e de um tronco de cone a partir de integrais triplas em coordenadas cilíndricas. Primeiro deduz a fórmula do volume de um cone circular reto como πR2H/3 e depois generaliza para o volume de um tronco de cone como πR2(H-hB)/3, onde R é o raio, H a altura total e hB a altura da base do tronco. Por fim, aplica as fórmulas ao cálculo do volume de um sól

1. Cálculo do Volume de um Sólido Geométrico a partir de Integrais Triplas em Coordenadas Cilíndricas 1 Anderson Iop 1 Diego Guarnieri Corrêa 1 Donizete de Gouvêa 2 Hudson Antonio de Sousa Junior 1 Discente do Curso de Engenharia da Computação 2 Discente do Curso de Engenharia Elétrica 3 Valdemir Antunes 3 Docente da Disciplina de Cálculo Diferencial e Integral II do Curso de Engenharia da Computação/Elétrica

2. Dedução da Fórmula do Volume de um Cone Circular Reto a partir de Integrais Triplas em Coordenadas Cilíndricas A partir da equação do cone: Vendo que o cone tem base circular é possível dizer que: (1) (2)

3. Dedução da Fórmula do Volume de um Cone Circular Reto a partir de Integrais Triplas em Coordenadas Cilíndricas Também pela equação (1), tem-se: Reescrevendo a equação (1): Onde R é o raio do Cone e H a altura. (3) (4)

4. Dedução da Fórmula do Volume de um Cone Circular Reto a partir de Integrais Triplas em Coordenadas Cilíndricas Pela equação (4) obtém-se a figura 1. Figura 1 - Cone

5. Dedução da Fórmula do Volume de um Cone Circular Reto a partir de Integrais Triplas em Coordenadas Cilíndricas Ainda pela equação (4), isolando “z”, E fazendo, (5) (6)

6. Dedução da Fórmula do Volume de um Cone Circular Reto a partir de Integrais Triplas em Coordenadas Cilíndricas Substituindo (6) em (5), Onde “z” esta em função de “r”, sendo que “H” e “R” são constantes. (7)

7. Dedução da Fórmula do Volume de um Cone Circular Reto a partir de Integrais Triplas em Coordenadas Cilíndricas A partir de uma integral triplas é possível o realizar o cálculo do volume do sólido. Utilizando coordenadas cilíndricas a integral fica:

8. Dedução da Fórmula do Volume de um Cone Circular Reto a partir de Integrais Triplas em Coordenadas Cilíndricas Substituindo os limites de integração a partir da figura 1, e usando simetria em relação a “z”, (8)

9. Dedução da Fórmula do Volume de um Cone Circular Reto a partir de Integrais Triplas em Coordenadas Cilíndricas

10. Dedução da Fórmula do Volume de um Cone Circular Reto a partir de Integrais Triplas em Coordenadas Cilíndricas Finalmente: Onde R é o raio do cone e H a altura do mesmo. (9)

11. Dedução da Fórmula do Volume de Tronco de Cone Fazendo um corte paralelo ao plano xy na figura 1 a uma distancia h B da base obtém-se: Figura 2 – Tronco de Cone

12. Dedução da Fórmula do Volume de Tronco de Cone O sólido restante do corte é a figura 3, Figura 3 – Cone da Base

13. Dedução da Fórmula do Volume de Tronco de Cone O volume da figura 2 pode ser calculado pela diferença do volume da figura 1 com o volume da figura 3, logo, Como Vc e Vcb são respectivamente, (10) (11) (12)

14. Dedução da Fórmula do Volume de Tronco de Cone Fazendo a figura 2 em 2D, Figura 4 – Cone em 2D

15. Dedução da Fórmula do Volume de Tronco de Cone Pela figura 4 e por semelhança de triângulos, Substituindo (13) em (14) e isolando “h B “, (14) (13) (15)

16. Dedução da Fórmula do Volume de Tronco de Cone Substituindo (11), (12), (13) e (15) em (10), Resolvendo, (16)

17. Resultado das Medidas do Sólido e Cálculo do Volume As medidas encontradas no sólido são as seguintes: 10,40 cm Altura do Tronco 10,45 cm Geratriz 2,37 cm Raio da Base 3,45 cm Raio da Boca 4,74 cm Diâmetro da Base 6,90 cm Diâmetro da Boca

18. Resultado das Medidas do Sólido e Cálculo do Volume Volume obtido utilizando a equação (16): V T = 279,58122 cm 3 ou V T = 279,58122 ml Medindo o volume do sólido obtém-se: V T = 280 ml

19. Referências Bibliográficas Swokowski, E. W. Cálculo com Geometria Analítica – volume 2 . São Paulo: Makron Books, 1994. p. 459 – 535. LEITHOLD, Louis. O Cálculo com Geometria Analítica – volume 2 . São Paulo: Harbra, 1994. p. 1023 – 1060. _________.Notas de Aula, da disciplina de Cálculo Diferencial e Integral II do Curso de Engenharia da Computação da Universidade Norte do Paraná, 2006.