O documento apresenta os conceitos e propriedades das integrais duplas, incluindo: (1) integrais duplas como extensão do conceito de integral definida para funções de duas variáveis, (2) exemplos de cálculo de integrais duplas, (3) propriedades das integrais duplas, e (4) cálculo de integrais duplas para domínios retangulares e não retangulares.

1. Ensino Superior
7. Integrais Duplas
Conceitos e Propriedades
Amintas Paiva Afonso
Cálculo 3

2. Integrais Duplas
• Integral dupla é uma extensão natural do conceito
de integral definida para as funções de duas
variáveis. Serão utilizadas para analisar diversas
situações envolvendo cálculo de áreas e volumes,
determinação de grandezas físicas e outros.

3. Exemplo 1

4. Exemplo 2
dx

5. Exemplo 3
( ) 2/32
3/2
2
2
1
3
1
3
u
-
du
2
1
2
1
-dr
2
1
dr.1
r
u
dur
dudrr
ur
rr
−−
−
=
=−
=−
−
∫
∫
θ

6. Exemplo 4

7. Exemplo 5

8. Exemplo 6

9. Exemplo 7
Calcule , onde R = [1, 2] x [0, π].
∫∫R
dAxyysen )(
∫∫ =R
dAxyy )sin( dydxxyy∫ ∫
2
1 0
)sin(
π
( )dxxyydx∫ ∫ −=
2
1 0
))(cos(1π
dxdyxyxyy xx∫ ∫+−=
2
1 00
])cos(|)cos([ 11 ππ
dxxyx xx∫ +−=
2
1 02 ]|)sin()cos([ 11 π
ππ dxx
x
x
x
∫ −=
2
1 2 ][
)cos()sin( πππ
∫−∫=
2
1
2
1 2
)cos()sin(
dxdx x
x
x
x πππ
∫−∫=
2
1
2
1 2
)sin()sin(
x
xd
x
x
dx ππ
∫−∫= −
 2
1 2
2
1 2
)sin(2
1
)sin()sin(
dxdx x
x
x
x
x
x πππ
0
2
1
)sin(
=−= 

x
xπ

10. Exemplo 8
Calcule a integral Iterada ( )
1 1
2
0
sin
x
y dy dx∫ ∫
D = {(x, y) / 0 ≤ x ≤ 1, x ≤ y ≤ 1}
( ) ( )
1 1
2 2
0
sin sin
x
D
y dy dx y dA=∫ ∫ ∫∫

11. Exemplo 8
Calcule a integral Iterada ( )
1 1
2
0
sin
x
y dy dx∫ ∫
D = {(x, y) / 0 ≤ y ≤ 1, 0 ≤ x ≤ y}
( ) ( )
1 1
2 2
0
sin sin
x
D
y dy dx y dA=∫ ∫ ∫∫

12. Exemplo 8
Calcule a integral Iterada ( )
1 1
2
0
sin
x
y dy dx∫ ∫
( ) ( )
( )
( )
( )
( )
1 1
2 2
0
1
2
0 0
1
2
00
1
2
0
121
2 0
1
2
sin sin
sin
sin
sin
cos
(1 cos1)
x
D
y
x y
x
y dy dx y dA
y dxdy
x y dy
y y dy
y
=
=
=
=
=   
=
= − 
= −
∫ ∫ ∫∫
∫ ∫
∫
∫

13. Exercícios
1) Calcule a integral abaixo onde R é o retângulo no plano xy
limitado pelo eixo x, pela reta y = x e pela reta x = 1.
dA
x
x
R
∫∫
sen
2) Resolver a integral dupla .∫ ∫ +
2
0
2
2
)24(.
x
x
dydxx
3) Integrar a função f(x,y), considerando o domínio definido
pelas retas x = 0, y = 0 e y = x. .

14. Propriedades das Integrais Duplas

15. Integrais Dupla para
Domínios Não Retangulares
 Múltiplo constante:
 Soma e diferença:
 Aditividade: (R = R1 + R2)
∫∫∫∫ =
RR
dxdyyxfkdxdyyxfk ),(),(.
∫∫∫∫∫∫ +=+
RRR
dxdyyxgdxdyyxfdxdyyxgyxf ),(),()],(),([
∫∫∫∫∫∫ +=
21
),(),(),(
RRR
dxdyyxfdxdyyxfdxdyyxf

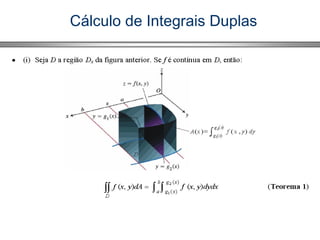
16. Cálculo de Integrais Duplas
Se f (x, y) é contínua no retângulo R = [a, b] × [c, d], a integral
dupla é igual a integral iterada.
a b
x
y
c
d
x
y
∫∫∫∫∫∫ ==
b
a
d
c
d
c
b
aR
dydxyxfdxdyyxfdAyxf ),(),(),(
fixo fixo

17. Cálculo de Integrais Duplas
a b
x
y
h(x)
g(x)
x
∫ ∫∫∫ =
b
a
xg
xhA
dydxyxfdAyxf
)(
)(
),(),(
A
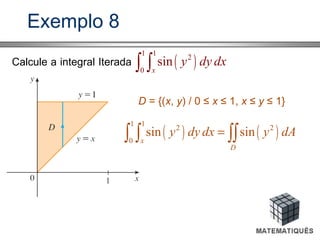
Se f (x, y) é contínua em A = {(x, y) / x em [a, b] e h(x) ≤ y ≤ g(x)},
a integral dupla é igual a integral iterada.

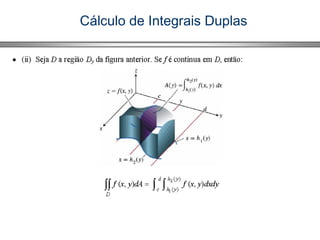
18. Cálculo de Integrais Duplas
d
x
y
∫ ∫∫∫ =
d
c
yg
yhR
dxdyyxfdAyxf
)(
)(
),(),(
c
h(y) g(y)
y
A
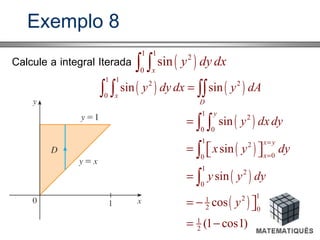
Se f (x, y) é contínua em A = {(x, y) / y em [c, d] e h(y) ≤ x ≤ g(y)},
a integral dupla é igual a integral iterada.

19. Cálculo de Integrais Duplas
∫ ∫ ∫==
b
a
b
a
xg
xg
dxdyyxfdxxAV
)(2
)(1
]),(.[)( ∫ ∫ ∫==
b
a
d
c
yh
yh
dydxyxfdyyAV
)(2
)(1
]),(.[)(

20. Integrais Duplas para
Domínios Não Retangulares
∫ ∫ ∫==
b
a
b
a
xg
xg
dxdyyxfdxxAV
)(2
)(1
]),(.[)(

21. Cálculo de Integrais Duplas

22. Integrais Dupla para
Domínios Não Retangulares
∫ ∫ ∫==
b
a
d
c
yh
yh
dydxyxfdyyAV
)(2
)(1
]),(.[)(

23. Cálculo de Integrais Duplas

24. Integrais Iteradas – Definição
∫ ∫
∫ ∫∫∫








=








=
d
c
b
a
b
a
d
cR
dydx)y,x(f
dxdy)y,x(fdA)y,x(f

25. Exercícios
Calcule onde D é a região limitada pelas parábolas
y = 2x2
e y = 1 + x2
.
∫∫ +
D
dA)y2x(
( )dxdyyx
x
x∫ ∫ += −
+1
1
1
2
2
2 )2(
( ) dxyxy
xy
xy
2
2
1
2
1
1
2
+=
=−∫ +=
( )dxxxxxx∫ −−+++= −
1
1
43222
42)1()1(
( )dxxxxx∫ +++−−= −
1
1
234
123
1
123
2
45
3
345
−






+++−−= x
xxxx
15
32
=

26. Exercícios
Resposta: 36
Calcule , onde D é a região limitada pela reta y = x – 1
e pela parábola y2
= 2x + 6.
∫∫
D
xydA

27. Exercícios
Calcule , onde D é a região limitada pela reta y = x – 1
e pela parábola y2
= 2x + 6.
∫∫
D
xydA
21
2
21
2
4 1
2 3
12
4
2
3
4
2 2 21 1
2 22
5
4
3 21
2 2
46 3
4 21
2
2
2
( 1) ( 3)
4 2 8
4
2 4 36
24 3
y
y
D
x y
x y
xydA xy dxdy
x
y dy
y y y dy
y
y y y dy
y y
y y
+
− −
= +
−
= −
−
−
−
=
 
=  
 
= + − −  
 
= − + + − ÷
 
 
= − + + − = 
 
∫∫ ∫ ∫
∫
∫
∫

28. Exercícios
Calcule , onde D é a região limitada pela reta y = x – 1
e pela parábola y2
= 2x + 6.
∫∫
D
xydA
1 2 6 5 2 6
3 2 6 1 1
x x
x x
D
xydA xy dy dx xy dy dx
− + +
− − + − −
= +∫∫ ∫ ∫ ∫ ∫

29. Exercícios

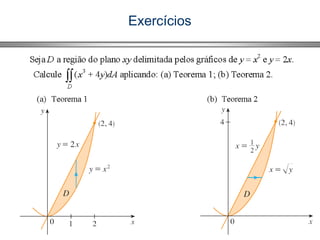
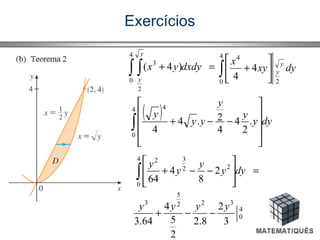
30. Exercícios
=+∫ ∫ )4(
2
0
2
3
2
dydxyx
x
x
dx
y
yx x
x∫ +
2
0
2
2
3
2)
2
4
(
[ ]dxxxxxxx∫ −−+
2
0
22323
)(2.)2(22
=∫ )8(
2
0
52
dx-xx 2
0
63
63
8 x
-
x
3
32
6
64
6
64
3
64
==-

31. Exercícios
=+∫ ∫ )4(
4
0
2
3
dxdyyx
y
y
dyxy
x y
y
2
4
0
4
4
4∫ 





+
( ) dyy
y
y
yy
y
∫ 









−−+
4
0
4
.
2
4
4
2.4
4
=








−−+∫ 2
8
4
64
4
0
22
32
dyy
y
y
y
4
0
322
5
3
3
2
8.2
2
5
4
64.3
yyyy
−−+

32. Exercícios
4
0
322
5
3
3
2
8.2
2
5
4
64.3
yyyy
−−+
4
0
322
5
3
3
2
165
8
192
yyyy
−−+
3
4.2
16
4
5
4.8
192
4 322
5
3
−−+
3
32
3
128
1
5
4.128
3
1
3
4.2
16
4
5
4.8
192
4 322
5
3
=−−+=−−+

33. Exercícios

34. Exercícios

35. Exercícios

36. Exercícios

37. Valor Médio de f(x,y) sobre o domínio R
∫ ∫
∫ ∫
∫∫ == b
a
d
c
b
a
d
c
R
dydx
dydxyxf
dxdyyxf
Rdeàrea
VM
),(
),(
..
1

38. Valor Médio de f(x,y) sobre o domínio R
Exemplo:
Calcular o valor médio da função f(x,y) = sen(x + y), no
retângulo 0 ≤ x ≤ π e 0 ≤ x ≤ π/2.