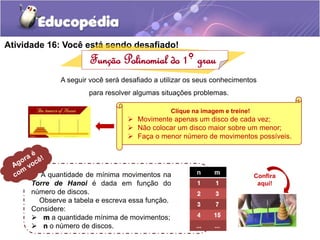
O documento apresenta uma aula sobre funções polinomiais do 1o grau. Nele, são discutidos conceitos como diagrama de flechas, produto cartesiano, domínio, contradomínio e imagem de uma função. Além disso, são fornecidos exercícios interativos para que o aluno teste seus conhecimentos sobre o assunto.
















![Atividade 15: Educoquiz 3 – O que mais você aprendeu?
O preço de venda de um livro é de R$ 25,00 a
unidade. Sabendo que o custo de cada livro corresponde a um
valor fixo de R$ 4,00 mais R$ 6,00 por unidade, construa uma
função capaz de determinar o lucro líquido (valor descontado
das despesas) na venda de x livros, e o lucro obtido na venda de
500 livros.
Considere: Venda = Receita [ R(x) ]
Fabricação = Custo [ C(x) ]
Receita – Custo = Lucro [ L (x) ]
( A ) L(x) = 21 x + 6 e R$ 10.506,00
( B ) L(x) = 21 x – 6 e R$ 10.494,00
( C ) L (x) = 19 x + 4 e R$ 9.504,00
( D ) L (x) = 19 x – 4 e R$ 9.496,00
GABARITO: Letra ( D )
Questão 4:.](https://image.slidesharecdn.com/funopolinomialdo1grau-140915180102-phpapp01/85/Funcao-polinomial-do-1-grau-23-320.jpg)