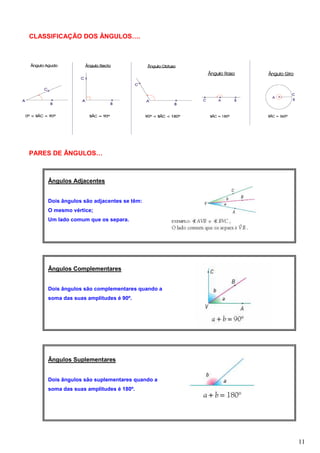
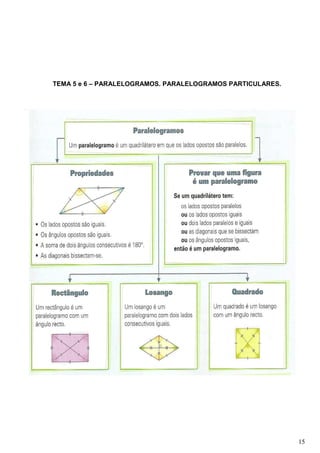
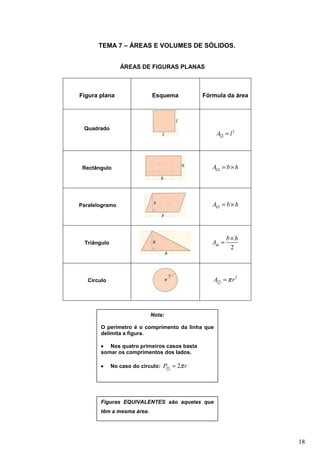
Este documento fornece informações sobre um plano de aula de matemática do 7o ano. Contém sete temas: 1) Posições relativas de retas e planos, 2) Triângulos, 3) Critérios de igualdade de triângulos, 4) Ângulos, 5) Paralelogramos, 6) Paralelogramos particulares, 7) Áreas e volumes de sólidos. Fornece definições-chave, atividades e exercícios para cada tema.

1. ESCOLA BÁSICA INTEGRADA ELIAS GARCIA
MATEMÁTICA – 7º ANO
FICHA INFORMATIVA E DE ACTIVIDADES
Unidade 6: Do Espaço ao Plano
Nome do Aluno: __________________________________________________Número:_____ Turma:_______
TEMA 1 – POSIÇÕES RELATIVAS DE RECTAS E PLANOS
1

2. EXERCÍCIOS SOBRE POSIÇÕES RELATIVAS DE RECTAS E PLANOS
2

3. TEMA 2 – TRIÂNGULOS. DESIGUALDADE TRIANGULAR.
3

4. DESIGUALDADE TRIANGULAR (REVISÃO 6ºANO)
4

5. EXERCÍCIOS SOBRE DESIGUALDADE TRIANGULAR.
5

6. CONSTRUÇÃO DE TRIÂNGULOS (REVISÃO 6ºANO)
6

7. EXERCÍCIOS SOBRE CONSTRUÇÃO DE TRIÂNGULOS
7

8. TEMA 3 – CRITÉRIOS DE IGUALDADE DE TRIÂNGULOS.
Dois triângulos são geometricamente iguais quando têm simultaneamente:
Os ângulos correspondentes iguais;
Os comprimentos dos lados correspondentes iguais.
Não é no entanto necessário conhecer todos os elementos de um triângulo (o comprimento dos três
lados e a amplitude dos três ângulos) para garantir a igualdade. Existem condições mínimas que
garantem a igualdade de dois triângulos – os critérios de igualdade de triângulos.
Vais construir alguns triângulos e concluir quais são essas condições mínimas.
Abre a página http://matti.usu.edu/nlvm/nav/frames_asid_165_g_3_t_3.html
ACTIVIDADE 1
1. Escolhe a opção SSS.
2. Com os três segmentos a vermelho tenta construir um triângulo, unindo as extremidades dos
segmentos.
- Move um segmento carregando e arrastando o seu ponto médio, utilizando o rato.
- Roda um segmento carregando e arrastando uma das extremidades.
3. Quando conseguires formar um triângulo, o seu interior fica colorido.
4. Repete os passos 2 e 3 para os segmentos a azul.
5. Depois de construíres os dois triângulos, sobrepõe um triângulo sobre o outro.
O que concluis? …………………………………………………………………
(LLL) CONCLUSÃO:
Para que dois triângulos sejam iguais, basta que os três ……………… de um sejam
………………… aos três lados do outro.
ACTIVIDADE 2
1. Escolhe a opção SAS.
2. Com os dois segmentos e o ângulo a vermelho tenta construir um triângulo, unindo a um dos
segmentos o ângulo e por fim o outro segmento.
3. Quando conseguires formar um triângulo, o seu interior fica colorido.
4. Repete os passos 2 e 3 para os segmentos e o ângulo a azul.
5. Depois de construíres os dois triângulos, sobrepõe um triângulo sobre o outro.
O que concluis? …………………………………………………………………
(LAL) CONCLUSÃO:
Para que dois triângulos sejam iguais basta que dois ……………… sejam iguais e o
……………… compreendido entre eles também seja igual.
8

9. ACTIVIDADE 3
1. Escolhe a opção ASA.
2. Com os dois ângulos e o segmento a vermelho tenta construir um triângulo.
3. Quando conseguires formar um triângulo, o seu interior fica colorido.
4. Repete os passos 2 e 3 para os ângulos e o lado a azul.
5. Depois de construíres os dois triângulos, sobrepõe um triângulo sobre o outro.
O que concluis? …………………………………………………………………
(ALA) CONCLUSÃO:
Para que dois triângulos sejam iguais basta que tenham um ………… igual e os dois
………………… adjacentes a esse lado iguais.
EXERCÍCIOS SOBRE CRITÉRIOS DE IGUALDADE DE TRIÂNGULOS
9

10. TEMA 4 – ÂNGULOS
10

11. CLASSIFICAÇÃO DOS ÂNGULOS….
PARES DE ÂNGULOS…
Ângulos Adjacentes
Dois ângulos são adjacentes se têm:
O mesmo vértice;
Um lado comum que os separa.
Ângulos Complementares
Dois ângulos são complementares quando a
soma das suas amplitudes é 90º.
Ângulos Suplementares
Dois ângulos são suplementares quando a
soma das suas amplitudes é 180º.
11

12. Ângulos Verticalmente Opostos
Vamos investigar as relações que existem entre ângulos formados por rectas.
Construímos duas rectas, AB e AC, como mostra a figura (o ponto A está em ambas as rectas).
As duas rectas concorrentes determinam dois pares de ângulos verticalmente opostos.
Ângulos verticalmente opostos são aqueles que têm o mesmo _________________ e em que os
___________ de um estão no prolongamento dos _____________ do outro.
D
B
A
E C
1. Assinala com a mesma cor dois ângulos agudos e mede as suas amplitudes.
O que verificas?
2. Assinala com outra cor dois ângulos obtusos e mede as suas amplitudes.
O que verificas?
3. Os ângulos ∠ BAC e ∠ CAE (um ângulo agudo e um ângulo obtuso ) dizem-se ângulos
suplementares. O nome advém do facto de existir uma relação entre eles. Qual é?
4. Conclusão:
Ângulos Verticalmente Opostos são___________________________________
Nota: Consulta o endereço:
http://moodle.ebiji-eliasgarcia.edu.pt/mod/resource/view.php?id=2122
e faz tu mesmo a experiência com os ângulos assinalados, movendo os seus lados…
12

13. Ângulos de Lados Paralelos
1. Construímos a recta AB e o ponto C que não pertence a AB.
C
A B
2. Depois, construímos a recta paralela a AB que passa por C e a recta AC.
C
A B
3. Marcamos os pontos D, E, F, G e H como mostra a figura.
E
D
C F
H
A B
G
4.a) Mede os oito ângulos da figura anterior e regista as suas amplitudes:
∠ ECF a sua amplitude é_______ ∠ CAB a sua amplitude é_______ ∠ FCA a sua amplitude é______
∠ BAG a sua amplitude é_______ ∠ ECD a sua amplitude é________ ∠ CAH a sua amplitude é_______
∠ DCA a sua amplitude é_______ ∠ HAG a sua amplitude é________.
b) Os ângulos ∠ ECF e ∠ CAB dizem-se ângulos de lados paralelos. Escreve todos os pares de
ângulos de ângulos de lados paralelos da figura anterior:
Agudos:_____________________________________________________________________
O que concluis?_____________________________________________________________________
Obtusos:____________________________________________________________________
O que concluis?_____________________________________________________________________
Um Agudo e Outro Obtuso:_____________________________________________________
O que concluis?_____________________________________________________________________
13

14. 5. Conclusão:
Dois ângulos de lados paralelos
Se forem da mesma espécie (ambos agudos ou ambos obtusos) são……………………..;
Se um for agudo e o outro obtuso, são ………………………………………………………….
Nota: Consulta o endereço:
http://moodle.ebiji-eliasgarcia.edu.pt/mod/resource/view.php?id=2920
e faz tu mesmo a experiência com os ângulos assinalados, movendo os seus lados…
EXERCÍCIOS SOBRE ÂNGULOS
14

15. TEMA 5 e 6 – PARALELOGRAMOS. PARALELOGRAMOS PARTICULARES.
15

16. EXERCÍCIOS SOBRE PARALELOGRAMOS
16

17. EXERCÍCIOS SOBRE PARALELOGRAMOS PARTICULARES
17

18. TEMA 7 – ÁREAS E VOLUMES DE SÓLIDOS.
ÁREAS DE FIGURAS PLANAS
Figura plana Esquema Fórmula da área
Quadrado
A□ = l 2
Rectângulo A▭ = b × h
Paralelogramo A▱ = b × h
b×h
Triângulo A△ =
2
Círculo A⊙ = π r 2
Nota:
O perímetro é o comprimento da linha que
delimita a figura.
• Nos quatro primeiros casos basta
somar os comprimentos dos lados.
• No caso do círculo: P⊙ = 2π r
Figuras EQUIVALENTES são aquelas que
têm a mesma área.
18

19. VOLUMES DE SÓLIDOS
PRISMAS CILINDRO
Cubo Paralelepípedo Outros prismas
V = Ab × h V = Ab × h V = Ab × h
ou ou ou
V = a3 V = a×b×c V = Ab × h V = π × r2 × h
Volume=Área da base × altura
PIRÂMIDES CONE
Ab × h 1 Ab × h 1
V = ou V = × Ab × h V = ou V = × π × r × h
2
3 3 3 3
1
Volume= × Área da base × altura
3
Sólidos EQUIVALENTES são aqueles que têm o
mesmo volume.
19

20. EXERCÍCIOS SOBRE ÁREAS E VOLUMES
1
1.1
.
1.2
.
2
2.1
.
2.2
2
3
Bom Trabalho!
Professora: Carla Varela
20