Aula 2 - Distribuição de probabilidade

Universidade Federal da Paraíba - Centro de Ciências Sociais Aplicadas - Programa de Pós-Graduação em Ciências Contábeis
Campus I - Cidade Universitária - CEP 58.051-900 - João Pessoa/PB
Telefone: +55 (83) 3216 7285 - http://ccsa.ufpb.br/ppgcc - e-mail: ppgcc@ccsa.ufpb.br
DISTRIBUIÇÕES DE
PROBABILIDADES E OUTLIERS
Felipe Pontes
www.contabilidademq.blogspot.com
1. Revisão do Exercício da aula passada 2. Ditribuições de
probabilidades (revisão de conceitos básicos) 3. Aplicação do
assunto da aula 1 e 2 com uma base de dados real

www.contabilidademq.blogspot.com Felipe Pontes 22
it
k
k
ktk
k
kitk
j
jitjit XCustosIncAD     1
,,2,,10
𝑃𝑡 =
𝜏=1
∞
𝑅𝑓−𝑡
𝐸𝜏 𝑑 𝑡+𝜏
youtube.com/contabilidademq
@felfelipepontes
@contabilidademq
Slideshare.net/felipepontes16
/pontesfelipe Se inscreva em nosso canal e
ative as notificações para não
perder nada!

INTRODUÇÃO
• Na aula passada vimos como descrever um conjunto de variáveis (estatísticas
descritivas). Isso nos permite identificar certos padrões e tendências. Vamos
discutir sobre as suas respostas da aula passada: 1) questões do livro, 2)
explicação rápida sobre as estatísticas descritivas de um artigo e 3) explicação
rápida sobre a análise descritiva dos dados da aula passada.
• ATENÇÃO: hoje faremos alguns exercícios. Façam de forma organizada em
uma planilha do Excel, ou no Word, e me enviem pela “tarefa” do SIGAA.
• Importância do assunto de hoje: o fundamento da tomada de decisões (teste de
hipóteses) é a probabilidade (LEVIN; FOX; FORD, 2012), pois envolve a incerteza.
• Probabilidade teórica (50% de chance de nascer homem) x Probabilidade
empírica (51% de chance de nascer homem com dados de longo prazo)
www.ccsa.ufpb.br/ppgcc ppgcc@ccsa.ufpb.br 3

DEFINIÇÃO:
• As variáveis econômicas são, por sua natureza, aleatórias. Não sabemos quais serão seus valores,
até observá-los (“experimentando”).
• Como são aleatórias, a ocorrência de seus valores é incerta. A probabilidade é uma forma de
expressar esta incerteza.
VARIÁVEL ALEATÓRIA X VARIÁVEL DE UMA EQUAÇÃO ALGÉBRICA
• 10 + X = 13 .:. X = 3 X é um valor desconhecido que pode ser calculado
• No processo de jogar 2 dados, a variável X pode ser qualquer valor entre 2 e 12
VARIÁVEIS ALEATÓRIAS

EXPERIMENTO CONTROLADO E NÃO CONTROLADO
• Controlado  variável não aleatória
• Não controlado  variável aleatória
“O Lado B do Insider Trading”: a) empresa sem operações dos insiders e b) empresa com operações dos
insiders (QI e QII)
Tudo é constante, exceto uma “variável”

• Sobre a importância dos experimentos, leiam o capítulo 2 do livro
Superprevisores.
• Apesar de não haver perfeição em nossas pesquisas, os experimentos são
melhores do que apenas “sabichões coçando o queixo” e pessoas com
“complexo de deus”.
• Para conhecer um pouco mais sobre o livro, leia a minha review lá no blog:
http://contabilidademq.blogspot.com.br/2017/03/review-superprevisores-
arte-e-ciencia-de-antecipar-o-futuro.html

• As variáveis aleatórias podem ser contínuas ou discretas. Classifique as
variáveis abaixo em um dos dois grupos.
Lançamento
de moedas
Retorno das
ações da bolsa
Quantidade de M&Ms azuis
Lançamento
de dados
Lucro das
empresas da
bolsa

• Para trabalhar com variáveis aleatórias e testar hipóteses, precisamos de
uma distribuição de probabilidades (contínuas ou discretas).
http://isomorphism.es/post/18913494015/probability-distributions

• No mundo real
• http://isomorphism.es/

DISTRIBUIÇÃO DE
PROBABILIDADES

DISTRIBUIÇÃO DE
PROBABILIDADES
• A é o resultado de um evento qualquer, a partir de um experimento não
controlado. A probabilidade de A, representada por P(A), é a frequência
relativa com que o resultado A ocorre em muitas provas repetidas do
experimento. Para qualquer evento, 0≤P(A)≤1 e Σp(A)= 1.
• Função de probabilidade – quando se relacionam os valores de uma
variável aleatória discreta com sua probabilidade de ocorrência, o
resultado é uma função de probabilidade. No caso de uma variável
continua temos a função densidade de probabilidade (f.d.p ou p.d.f).

NORMAL
• É um modelo teórico (ou ideal) muito usado em econometria básica (foco
desta disciplina). Por meio dela o pesquisador pode generalizar seus
resultados de amostras para populações.
CARACTERÍSTICAS BÁSICAS:
1. Formato de sino
2. Simétrica
3. Unimodal (só tem um pico de máxima probabilidade)
4. Média = Moda = Mediana
https://www.mathsisfun.com/data/standard-normal-distribution.html
IMPLICAÇÃO: por exemplo, teríamos poucas
empresas com retornos extremos (positivos ou
negativos) – as empresas não devem gerar lucros
“anormais” para sempre.

NORMAL
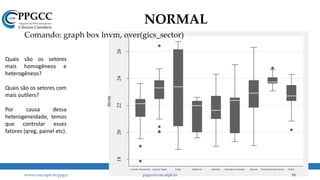
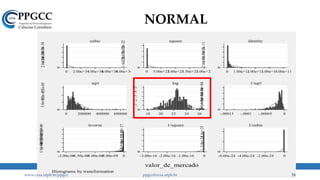
• Na prática, o que encontramos são coisas assim:
0
2
4
6
8
10
12
14
16
18
20
-0.1 0 0.1 0.2 0.3
acc_disc_abs
acc_disc_abs
N(0.036252,0.051882)
Test statistic for normality:
Chi-square(2) = 356.744 [0.0000]
0
5
10
15
20
25
30
0.00 0.05 0.10 0.15 0.20 0.25 0.30
Series: ACC_DISC_ABS
Sample 1 89
Observations 89
Mean 0.036252
Median 0.020848
Maximum 0.334798
Minimum 6.94e-18
Std. Dev. 0.051882
Skewness 3.665601
Kurtosis 18.70847
Jarque-Bera 1114.363
Probability 0.000000
05
101520
0 .1 .2 .3 .4
acc_disc_abs
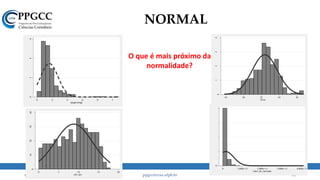
A assimetria é muito maior do que 0,5.
Regra geral: -0,5 < Skew < 0,5.
A Normal tem curtose = 3.
A partir dessa análise, o que pode ter
gerado nosso “problema”?
No Eviews, GRETL e Stata.

NORMAL
0246
Density
0 .2 .4 .6 .8 1
rpegaverage
0
10203040
Frequency
0 5 10 15 20
cob_eps
0
.1.2.3.4
Density
18 20 22 24 26
lnvm
O que é mais próximo da
normalidade?
0
1.0e-112.0e-113.0e-114.0e-11
Density
0 1.000e+11 2.000e+11 3.000e+11 4.000e+11
valor_de_mercado

NORMAL
0
.1.2.3.4
Os pontos fora da “caixa” são outliers
(maiores que 0,1 nesse caso)
A linha dentro da caixa é a mediana, como não
está no meio... Evidencia assimetria.
O limite superior da caixa indica o percentil 75%
e o limite inferior representa 25%.
O “bigode” de cima é o limite superior = P75% -
1,5*(P75% - P25%)
O “bigode” de baixo é o limite inferior = P25% -
1,5*(P75% - P25%)

0
.2.4.6.8
1
NORMAL
Os pontos fora da “caixa” são outliers
(maiores que 0,4 nesse caso)
A linha dentro da caixa é a mediana, como não
está no meio... Evidencia assimetria.
O limite superior da caixa indica o percentil 75%
e o limite inferior representa 25%.
O “bigode” de cima é o limite superior = P75% -
1,5*(P75% - P25%)
O “bigode” de baixo é o limite inferior = P25% -
1,5*(P75% - P25%)

NORMAL
1820222426
O que dizer sobre isso?
05
101520
cob_eps

1820222426
lnvm
Consumer Discretionary Consumer Staples Energy Health Care Industrials Information Technology Materials Telecommunication Services Utilities
NORMAL
Comando: graph box lnvm, over(gics_sector)
Quais são os setores
mais homogêneos e
heterogêneos?
Quais são os setores com
mais outliers?
Por causa dessa
heterogeneidade, temos
que controlar esses
fatores (qreg, painel etc).

NORMAL
• Se a distribuição for normal, os pontos ficarão em cima da reta
-.1
0
.1.2.3
acc_disc_abs
-.1 -.05 0 .05 .1 .15
Inverse Normal

NORMAL
1820222426
lnvm
18 20 22 24 26
Inverse Normal
-5
05
101520
cob_eps
-5 0 5 10 15 20
Inverse Normal
Quem é discreto e quem é contínuo?

NORMAL
• Algumas vezes, transformações resolvem nosso problema: log 10, ln, sqrt
(assimetria à direita), quadrática, cúbica (assimetria à esquerda) etc.
• Plotem o histograma da variável vm (valor de mercado) (histogram vm).
Qual é o tipo de assimetria? Depois compare com o histograma da variável
lnvm.
• O comando para transformar a variável é “generate
NOME_DA_NOVA_VARIÁVEL=TIPO_DE_TRANSF(inserir a variável a
ser transformada)”
• generate lnvm=ln(vm)

NORMAL
1/cubic 1/(vm^3) . 0.000
1/square 1/(vm^2) . 0.000
inverse 1/vm . 0.000
1/(square root) 1/sqrt(vm) . 0.000
log log(vm) 3.25 0.197
square root sqrt(vm) . 0.000
identity vm . 0.000
square vm^2 . 0.000
cubic vm^3 . 0.000
Transformation formula chi2(2) P(chi2)
. ladder vm
O comando ladder do Stata nos diz qual é a melhor transformação (você não precisa ficar
calculando uma por uma). Faça com a variável vm.

NORMAL
1/cubic 1/(lnvm^3) 47.04 0.000
1/square 1/(lnvm^2) 31.10 0.000
inverse 1/lnvm 18.07 0.000
1/(square root) 1/sqrt(lnvm) 12.80 0.002
log log(lnvm) 8.51 0.014
square root sqrt(lnvm) 5.26 0.072
identity lnvm 3.25 0.197
square lnvm^2 5.77 0.056
cubic lnvm^3 15.44 0.000
. ladder lnvm

NORMAL
0
2.0e-344.0e-346.0e-348.0e-34
0 2.00e+344.00e+346.00e+348.00e+34
cubic
0
1.0e-222.0e-223.0e-224.0e-22
0 5.00e+221.00e+231.50e+232.00e+23
square
0
2.0e-114.0e-116.0e-118.0e-11
0 1.00e+112.00e+113.00e+114.00e+11
identity
0
5.0e-061.0e-051.5e-05
0 200000 400000 600000
sqrt
0
.1.2.3.4.5
18 20 22 24 26
log
0
2.0e+044.0e+046.0e+048.0e+04
-.00015 -.0001 -.00005 0
1/sqrt
0
5.0e+081.0e+091.5e+092.0e+092.5e+09
-2.00e-08-1.50e-08-1.00e-08-5.00e-09 0
inverse
0
5.0e+161.0e+171.5e+172.0e+17
-3.00e-16 -2.00e-16 -1.00e-16 0
1/square
0
5.0e+241.0e+25
-6.00e-24 -4.00e-24 -2.00e-24 0
1/cubic
Density
valor_de_mercado
Histograms by transformation

NORMAL
• O gladder projeta os tipos de transformações
0
1.0e-042.0e-043.0e-044.0e-04
5000 10000 15000 20000
cubic
0
.002.004.006.008
.01
300 400 500 600 700
square
0
.1.2.3.4.5
18 20 22 24 26
identity
012345
4.2 4.4 4.6 4.8 5 5.2
sqrt
05
10
2.9 3 3.1 3.2 3.3
log
0
20406080
100
-.24 -.23 -.22 -.21 -.2 -.19
1/sqrt
0
50
100150200250
-.055 -.05 -.045 -.04 -.035
inverse
0
100020003000
-.003 -.0025 -.002 -.0015
1/square
0
1.0e+042.0e+043.0e+044.0e+04
-.0002 -.00015 -.0001 -.00005
1/cubic
Density
lnvm

NORMAL
1/cubic 1/(cob_eps^3) . .
1/square 1/(cob_eps^2) . .
inverse 1/cob_eps . .
1/(square root) 1/sqrt(cob_eps) . .
log log(cob_eps) . .
square root sqrt(cob_eps) 43.48 0.000
identity cob_eps 63.13 0.000
square cob_eps^2 34.52 0.000
cubic cob_eps^3 42.33 0.000
. ladder cob_eps Por que será que nenhuma transformação deu jeito? Pense e
confirme o raciocínio no próximo slide

NORMAL
• Dá para perceber a diferença com relação aos gráficos anteriores?
0
5.0e-04
.001
.0015
.002
.0025
0 2000 4000 6000
cubic
0
.005
.01
.015
.02
.025
0 100 200 300
square
0
.1.2.3
0 5 10 15 20
identity
0
.5
1
1.5 0 1 2 3 4
sqrt
cob_eps

NORMAL
NO SLIDE ANTERIOR ESTÁVAMOS
TENTANDO ADEQUAR UMA
VARIÁVEL DISCRETA A UMA
DISTRIBUIÇÃO CONTÍNUA!

5000
100001500020000
5000 10000 15000 20000
cubic
300400500600700
300 400 500 600 700
square
1820222426
18 20 22 24 26
identity
4.24.44.64.8
5
5.2
4.2 4.4 4.6 4.8 5 5.2
sqrt
2.9
3
3.13.23.3
2.9 3 3.1 3.2 3.3
log
-.24-.23-.22-.21
-.2
-.19
-.23 -.22 -.21 -.2 -.19
1/sqrt
-.055
-.05
-.045
-.04
-.035
-.055 -.05 -.045 -.04 -.035
inverse
-.003
-.0025
-.002
-.0015
-.001
-.003 -.0025 -.002 -.0015 -.001
1/square
-.0002
-.00015
-.0001
-.00005
-.00014-.00012-.0001-.00008-.00006-.00004
1/cubic
lnvm
Quantile-Normal plots by transformation
NORMAL
• Para verificar o gráfico da normal, pode-se utilizar o qladder

-2.00e+34
0
2.00e+344.00e+346.00e+34 -1.00e+34-5.00e+33 0 5.00e+331.00e+341.50e+34
cubic
-5.00e+22
0
5.00e+221.00e+231.50e+23
-4.00e+22-2.00e+22 0 2.00e+224.00e+22
square
-1.00e+11
0
1.00e+112.00e+113.00e+114.00e+11
-1.00e+11-5.00e+10 0 5.00e+101.00e+111.50e+11
identity
-200000
0
200000400000600000
-100000 0 100000200000300000
sqrt
1820222426
18 20 22 24 26
log
-.00015
-.0001
-.00005
0
.00005
-.00006 -.00004 -.00002 0 .00002
1/sqrt
-2.00e-08-1.50e-08-1.00e-08-5.00e-09
0
5.00e-09
-4.00e-09-2.00e-09 0 2.00e-094.00e-09
inverse
-3.00e-16-2.00e-16-1.00e-16
0
1.00e-16
-4.00e-17-2.00e-17 0 2.00e-174.00e-17
1/square
-6.00e-24-4.00e-24-2.00e-24
0
2.00e-24
-1.00e-24-5.00e-25 0 5.00e-251.00e-24
1/cubic
valor_de_mercado

-2000
0
200040006000
-2000 0 2000 4000 6000
cubic
-100
0
100200300
-100 0 100 200 300
square
-5
05
101520
-5 0 5 10 15 20
identity
0246
0 2 4 6
sqrt
cob_eps

NORMAL
• É importante fazer essa análise antes de rodar o modelo final, para
detectar os problemas e tratá-los, se possível ou ter ideia das possíveis
limitações da sua análise: usar outros estimadores que não o OLS, por
exemplo.
• Esses gráficos precisam estar na versão final do artigo? Definitivamente
Não!

NORMAL
• Utilize os seguintes comandos com os dados do “sysuse nlsw88, clear”.
Analise a variável wage e tenure.
• Analise brevemente e salve os gráficos em um arquivo do Word, no final
faremos um exercício completo:
• histogram wage, normal
• graph box wage
• qnorm wage
• ladder wage
• gladder wage
• sktest wage
• ** testa a normalidade univariada
• ** Use transformações para testar, a exemplo de:
• g logwage=log(wage) ou lnwage=ln(wage)

NORMAL
ESCORE PADRÃO (Z) E A CURVA NORMAL
• O Z-escore nos diz quantos desvios-padrão um valor X está acima ou
abaixo da média.
• Tem algumas utilidades quando trabalhamos com a Normal e também é
utilizado para identificar outliers univariados (geralmente 3 DP da média
– mas fiquem de olho no tamanho da amostra, as pequenas são mais
sensíveis). Também é usada para tratar o efeito do uso de diferentes
escalas na análise multivariada.
• Para identificar outliers com o Z-escore, presume-se a normalidade dos
dados. Quando os dados não são normalmente distribuídos, o box-plot é
uma ferramenta melhor para detectá-los.

NORMAL
http://resources.esri.com/

NORMAL
ESCORE PADRÃO (Z) E A CURVA NORMAL
• Supondo que os dados são normalmente distribuídos e que têm média 9,5
e desvio-padrão de 17, qual é o Z-Escore de uma observação X = 53?
• Calcule o Z-Escore da variável FCO, na planilha “Pasta 1”, de modo a
encontrar possíveis outliers.
• Quais são os outliers, usando 2 DP da média, por ser uma amostra
pequena?

NORMAL
• Como padronizar variáveis no Stata, com o Z-escore (exemplo com Wage):
• sum wage
• ** A média foi 7.766949 e o desvio-padrão foi 5.755523. Aplicamos isso
na fórmula do Z-escore para padronizar a variável, fazendo com que
ela fique com média zero e variância constante
• ** Crio a nova variável
• g Zwage=(wage-7.766949)/5.755523
• ** Verificando:
• sum Zwage
• Para calcular o Z-Escore, existe também a função “padronizar” no Excel.

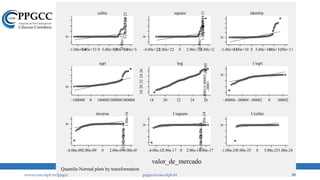
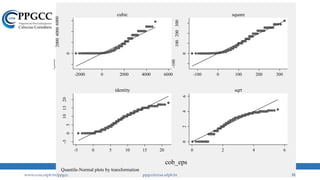
AMOSTRAS E POPULAÇÕES
• A contabilidade é uma ciência social aplicada, isso implica dizer que temos
tempo e recursos escassos (por exemplo não dá para entrevistar todos os
auditores do mundo). Para tirar nossas conclusões, partimos de um grupo
pequeno de indivíduos (amostra) e fazemos inferências sobre o grupo de
todos os indivíduos (população).
• Amostragem aleatória x não aleatória (intencional)
• O resultado obtido na amostragem dificilmente será
igual ao da população, devido ao “erro amostral”.
Todos têm a mesma chance de
estar na amostra
Não estamos falando de “erro intencional”: cada amostra terá características
“próprias”, mas não intencionais. Ex.: QIC apenas em empresas do Novo Mercado

INTERVALO DE CONFIANÇA
• Nós convencionamos usar 95% como nível de confiança (Z = 1,96 para cada lado,
– 47,5% e + 47,5% = 95% - VER NA TABELA NORMAL = 5%/2 = 2,5%).
• Mesmo usando os 95% de nível de confiança, podemos ter a “sorte” de selecionar
uma amostra que gere uma média dentro dos 5% restantes. Exemplo com várias
amostras da idade da turma.
• Calcule a média do FCO e utilize o nível de 95% para estimar um intervalo de
confiança: Média amostral + ou – 1,96*[DP/(N^0,5)]. Considere que o desvio-
padrão da amostra é igual ao da população.
• Considerando que a um nível de significância de 90% o Z é 1,645 (90%/2 = 0,45 
buscando 0,45 na Tabela Normal, temos 1,645 aproximadamente), estime o IC do
FCO.
• Agora considere um nível de 99% (Z = 2,575) para o mesmo FCO.

DISTRIBUIÇÃO t
• Anteriormente consideramos que sabíamos o desvio-padrão da população.
Isso faz pouco sentido!
• Para poder usar o DP amostral, basta utilizar o ajuste nos graus de
liberdade que vimos na aula passada: Média amostral + ou – t*{DP/[(N –
1)^0,5]}.
• Em amostras grandes isso faz pouca diferença. À medida que aumentamos
os GL a t tende à normal.
• A tabela t de Student é um pouco diferente da normal, ela usa os GL (N-1)
e o alfa. Lembrem de dividir por 2, porque estamos falando de duas
caudas.
• Refaça os exercícios do slide anterior, considerando a tabela t.

APLICAÇÃO 1
• Vamos usar outras metodologias de detecção de outliers.
• Use a base “dados para aula de normalidade” para detector outliers na
variável “rpegaverage”, comparando com a variável “cob_eps”:
• sum rpegaverage cob_eps
• extremes rpegaverage cob_eps
• scatter rpegaverage cob_eps

APLICAÇÃO 2
• Utilize a base de dados da aula de hoje (Plan1) para efetuar uma análise
descritiva (estatísticas descritivas, testes de normalidade, detecção de
outliers etc).
• Escreva um relatório, como se fosse um artigo. Por isso vocês analisaram
as estatísticas descritivas de um artigo na semana passada!

Questões para a próxima aula
1. Por que experimentos controlados são importantes?
2. Defina variáveis aleatórias e diferencie as contínuas das discretas.
3. Como calcular o valor esperado de uma variável aleatória?
4. Cite 2 exemplos de experimentos controlados. 1 deles deve ser um artigo
publicado em uma revista A1, A2 ou B1.
5. Cite algumas maneiras de se “induzir” a normalidade dos dados (não se limite
aos slides). A ideia é buscar maneiras de se “corrigir” esse problema.
6. Diferencie amostragem aleatória da não aleatória. Quais são as vantagens e
desvantagens de cada uma delas?
7. O que é amostragem por cotas, por julgamento, aleatória simples, sistemática e
estratificada?
8. Como se pode estimar o tamanho de uma amostra confiável?

Para ter acesso a mais conteúdos,
acesse:
• Blogs
www.ContabilidadeMQ.blogspot.com
www.FinancasAplicadasBrasil.blogspot.com
• Facebook:
www.facebook.com/ContabilidadeMQ
• Twitter:
www.twitter.com/ContabilidadeMQ
• YouTube:
www.youtube.com/ContabilidadeMQ
44

it
k
k
ktk
k
kitk
j
jitjit XCustosIncAD     1
,,2,,10
𝑃𝑡 =
𝜏=1
∞
𝑅𝑓−𝑡
𝐸𝜏 𝑑 𝑡+𝜏
youtube.com/contabilidademq
@felfelipepontes
@contabilidademq
Slideshare.net/felipepontes16
/pontesfelipe Se inscreva em nosso canal e
ative as notificações para não
perder nada!

Aula 2 - Distribuição de probabilidade

Mais conteúdo relacionado

Mais procurados

Semelhante a Aula 2 - Distribuição de probabilidade

Mais de Felipe Pontes

Aula 2 - Distribuição de probabilidade