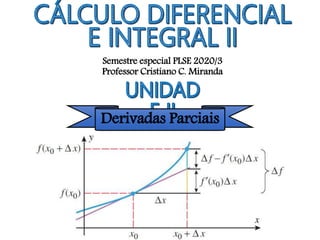
Derivadas Parciais de Funções de Duas Variáveis
- 1. Semestre especial PLSE 2020/3 Professor Cristiano C. Miranda Derivadas Parciais
- 2. Introdução De modo resumido, derivada é a taxa de crescimento pontual de uma função, para o caso de uma ou várias variáveis. Essa taxa pode ser positiva ou negativa, o que indica, respectivamente, se a função está ganhando ou perdendo valor. tan 𝛼 = lim ℎ→0 𝑓 𝑎 + ℎ − 𝑓 𝑎 ℎ = 𝑓′(𝑎)
- 3. Introdução A interpretação geométrica da derivada de função de uma variável é a inclinação de uma reta tangente ao gráfico da função. Veja como a derivada explica a forma de crescimento da função 𝑓(𝑥)
- 4. Introdução Para o caso de funções de duas variáveis, a derivada pode representar a inclinação de um plano tangente ao gráfico da função.
- 5. Motivação O índice Humidex (I) Em um dia quente, a umidade muito alta aumenta a sensação de calor, ao passo que, se o ar está muito seco, temos a sensação de temperatura mais baixa do que a indicada no termômetro. O Serviço Meteorológico do Canadá introduziu o humidex (ou índice de temperatura-umidade) para descrever os efeitos combinados da temperatura e umidade. O humidex 𝐼 é a temperatura aparente do ar quando a temperatura real for 𝑇 e a umidade relativa for 𝐻. Desse modo, 𝐼 é uma função de 𝑇 e 𝐻 e podemos descrever 𝐼 = 𝑓 (𝑇, 𝐻). Índice de calor 𝐼 como uma função de temperature 𝑇 e umidade 𝐻. 𝒙𝒚
- 6. A tabela de valores de I a seguir é a parte de uma tabela compilada pelo Serviço Meteorológico. Motivação Índice de calor I como uma função de temperatura e umidade Por hora, tomaremos como exemplo o valor 𝑓 30, 60 = 38 Veja que se fixarmos um valor de 𝑇 = 30 a função dependerá apenas de H. Se torna uma função de uma variável 𝒚 𝑯 = 𝒇(𝟑𝟎, 𝑯), ou seja o índice 𝑰 varia conforme caminha-se na direção de 𝑯
- 7. A tabela de valores de I a seguir é a parte de uma tabela compilada pelo Serviço Meteorológico. Motivação Índice de calor I como uma função de temperatura e umidade Pela definição, já sabemos como calcular a derivada de 𝑦(𝐻). 𝑦′ 60 = lim ℎ→0 𝑦 60+ℎ −𝑦 60 ℎ Usaremos os dados da tabela para estimar esse limite
- 8. Motivação Índice de calor I como uma função de temperatura e umidade 𝑦′ 60 ≈ 𝑦 65 − 𝑦 60 5 = 40 − 38 5 = 0,4 𝑦′ 60 ≈ 𝑦 55 − 𝑦 60 −5 = 37 − 38 −5 = 0,2 Para fazer a aproximação do valor da derivada, vamos analisar o valor de 𝑦′ 60 ≈ 𝑦 60+ℎ −𝑦 60 ℎ à direita e a esquerda de 𝐻 = 60 Se o incremento ℎ = 5 temos: Se o incremento ℎ = −5 temos: 60+560-5 Fazendo a média temos que a taxa de crescimento pontual do índice 𝐼 é 0,4+0,2 2 = 0,3, ou seja 𝐼 aumenta 0,3°𝐶 para cada percentual de 𝐻.
- 9. Motivação Uma representação gráfica dessa situação fica da seguinte forma: 𝑦′ 60 ≈ 𝑦 65 − 𝑦 60 5 = 40 − 38 5 = 0,4 𝑦′ 60 ≈ 𝑦 55 − 𝑦 60 −5 = 37 − 38 −5 = 0,2
- 10. Motivação Índice de calor I como uma função de temperatura e umidade Podemos fazer uma estimativa para derivada de 𝑓(𝑇, 𝐻) na direção de 𝑇. Basta fixar 𝐻 = 60 e definir 𝑓 𝑇, 60 = 𝑥(𝑇) como uma função que depende apenas de 𝑇. 𝑥′ 30 = lim ℎ→0 𝑥 30 + ℎ − 𝑥 30 ℎ 𝑥′ 30 ≈ 𝑥 32 − 𝑥 30 2 = 42 − 38 2 = 2 𝑥′ 30 ≈ 𝑥 28 − 𝑥 30 −2 = 35 − 38 −2 = 1,5 Se o incremento ℎ = 2 temos: Se o incremento ℎ = −2 temos: Basta fazer a média aritmética para determinar qual é a aproximação da derivada 𝒙′ 𝟑𝟎 ≈ 𝟐 + 𝟏, 𝟓 𝟐 = 𝟏, 𝟕𝟓
- 11. Definição Calculamos até então 𝑦′(60) e 𝑥′ 30 : 𝑦′ 60 = lim ℎ→0 𝑦 60+ℎ −𝑦 60 ℎ ≈ 0,3 e 𝑥′ 30 = lim ℎ→0 𝑥 30+ℎ −𝑥 30 ℎ ≈ 1,75 Porém, pode-se ver que 𝑦 60 + ℎ = 𝑓(30, 60 + ℎ), e 𝑦 60 = 𝑓(30, 60) Assim podemos reescrever 𝑦′ 60 = lim ℎ→0 𝑓 30, 60+ℎ −𝑓 30, 60 ℎ = 𝑓𝐻 ′ 30, 60 ≈ 0,3 E também reescrever 𝑥′ 30 = lim ℎ→0 𝑓 30+ℎ, 60 −𝑓 30, 60 ℎ = 𝑓𝑇 ′ 30, 60 ≈ 1,75 Generalizando: 𝑓𝑇 ′ 𝑎, 𝑏 = lim ℎ→0 𝑓 𝑎 + ℎ, 𝑏 − 𝑓 𝑎, 𝑏 ℎ ; 𝑓𝐻 ′ (𝑎, 𝑏) = lim ℎ→0 𝑓 𝑎, 𝑏 + ℎ − 𝑓 𝑎, 𝑏 ℎ Derivada de 𝒇(𝑻, 𝑯) no ponto (𝒂, 𝒃) na direção 𝑻 Derivada de 𝒇(𝑻, 𝑯) no ponto (𝒂, 𝒃) na direção 𝑯
- 12. Definição Seja 𝒇(𝒙, 𝒚) uma função 𝒇: 𝑹 𝟐 → 𝑹. Pode-se calcular as Derivadas Parciais no ponto (𝒂, 𝒃) nas direção de 𝒙, 𝒇 𝒙 ′ 𝒂, 𝒃 = 𝐥𝐢𝐦 𝒉→𝟎 𝒇 𝒂 + 𝒉, 𝒃 − 𝒇 𝒂, 𝒃 𝒉 , e de 𝒚, 𝒇 𝒚 ′ 𝒂, 𝒃 = 𝒍𝒊𝒎 𝒉→𝟎 𝒇 𝒂, 𝒃 + 𝒉 − 𝒇 𝒂, 𝒃 𝒉 . As funções Derivadas Parciais ficam: 𝒇 𝒙 ′ 𝒙, 𝒚 = 𝐥𝐢𝐦 𝒉→𝟎 𝒇 𝒙 + 𝒉, 𝒚 − 𝒇 𝒙, 𝒚 𝒉 , 𝒇 𝒚 ′ 𝒙, 𝒚 = 𝐥𝐢𝐦 𝒉→𝟎 𝒇 𝒙, 𝒃 + 𝒉 − 𝒇 𝒙, 𝒚 𝒉 .
- 13. Exemplos 1. Seja 𝒇 𝒙, 𝒚 = 𝟗 − 𝒙 𝟐 − 𝒚 𝟐. Encontre as derivadas parciais no ponto 𝟏, −𝟏 . Podemos repetir o que fizemos no caso da função Humidex. Quando fixamos 𝑥 = 1 temos: 𝑓 1, 𝑦 = 8 − 𝑦2 = 𝑔(𝑦), ou seja, uma função de uma variável. Sua derivada para 𝑦 = −1 fica: 𝑔′ (−1) = lim ℎ→0 𝑔 −1 + ℎ − 𝑔 −1 ℎ = lim ℎ→0 8 − −1 + ℎ 2 − 7 ℎ = = lim ℎ→0 8 − 1 − 2ℎ + ℎ2 − 7 ℎ = lim ℎ→0 (2 − ℎ) = 2 Também podemos usar o seguinte método equivalente: 𝑓𝑦 1, −1 = lim ℎ→0 𝑓 1, −1 + ℎ − 𝑓 1, −1 ℎ = lim ℎ→0 8 − −1 + ℎ 2 − 7 ℎ , 𝑓𝑦 1, −1 = 2
- 14. Exemplos 1. Seja 𝒇 𝒙, 𝒚 = 𝟗 − 𝒙 𝟐 − 𝒚 𝟐. Encontre as derivadas parciais no ponto 𝟏, −𝟏 . Do mesmo modo, quando fixamos 𝑦 = −1 temos: 𝑓 𝑥, −1 = 8 − 𝑥2 = ℎ(𝑥), ou seja, uma função de uma variável. Sua derivada para x = 1 fica: ℎ′ 1 = lim ℎ→0 ℎ 1 + ℎ − ℎ 1 ℎ = lim ℎ→0 8 − 1 + ℎ 2 − 7 ℎ = = lim ℎ→0 8 − 1 + 2ℎ + ℎ2 − 7 ℎ = lim ℎ→0 −2 − ℎ = −2 Também podemos usar o seguinte método equivalente: 𝑓𝑥 1, −1 = lim ℎ→0 𝑓 1 + ℎ, −1 − 𝑓 1, −1 ℎ = lim ℎ→0 8 − 1 + ℎ 2 − 7 ℎ , 𝑓𝑥 1, −1 = −2
- 15. 𝐥𝐢𝐦 𝒉→𝟎 − 𝟐𝒙 − 𝒉 𝒉 𝒉 = 2. Seja 𝒇 𝒙, 𝒚 = 𝟗 − 𝒙 𝟐 − 𝒚 𝟐. Encontre as derivadas parciais de primeira ordem. Usando a definição da função derivada parcial, 𝒇 𝒙 𝒙, 𝒚 = 𝐥𝐢𝐦 𝒉→𝟎 𝒇 𝒙 + 𝒉, 𝒚 − 𝒇 𝒙, 𝒚 𝒉 , Temos para a função 𝒇 𝒙: 𝐥𝐢𝐦 𝒉→𝟎 𝟗 − 𝒙 𝟐 − 𝟐𝒙𝒉 − 𝒉 𝟐 − 𝒚 𝟐 − 𝟗 + 𝒙 𝟐 + 𝒚 𝟐 𝒉 = Exemplos 𝐥𝐢𝐦 𝒉→𝟎 − 𝟐𝒙 − 𝒉 = −𝟐𝒙 𝒇 𝒙 𝒙, 𝒚 = −𝟐𝒙 𝒇 𝒙 𝒙, 𝒚 = 𝐥𝐢𝐦 𝒉→𝟎 𝟗 − 𝒙 + 𝒉 𝟐 − 𝒚 𝟐 − (𝟗 − 𝒙 𝟐 − 𝒚 𝟐) 𝒉 =
- 16. 2. Seja 𝒇 𝒙, 𝒚 = 𝟗 − 𝒙 𝟐 − 𝒚 𝟐. Encontre as derivadas parciais de primeira ordem. Usando a definição da função derivada parcial, 𝒇 𝒚 𝒙, 𝒚 = 𝐥𝐢𝐦 𝒉→𝟎 𝒇 𝒙, 𝒚 + 𝒉 − 𝒇 𝒙, 𝒚 𝒉 , Temos para a função 𝒇 𝒚: 𝐥𝐢𝐦 𝒉→𝟎 − 𝟐𝒚 − 𝒉 𝒉 𝒉 =𝐥𝐢𝐦 𝒉→𝟎 𝟗 − 𝒙 𝟐 − 𝒚 𝟐 − 𝟐𝒚𝒉 − 𝒉 𝟐 − 𝟗 + 𝒙 𝟐 + 𝒚 𝟐 𝒉 = Exemplos 𝐥𝐢𝐦 𝒉→𝟎 − 𝟐𝒚 − 𝒉 = −𝟐𝒚 𝒇 𝒚 𝒙, 𝒚 = −𝟐𝒚 𝒇 𝒚 𝒙, 𝒚 = 𝐥𝐢𝐦 𝒉→𝟎 𝟗 − 𝒙 𝟐 − (𝒚 + 𝒉) 𝟐−(𝟗 − 𝒙 𝟐 − 𝒚 𝟐) 𝒉 =
- 17. RESUMO DOS EXEMPLOS Exemplos 𝒇 𝒙 𝟏, −𝟏 = −𝟐 𝒇 𝒚 𝟏, −𝟏 = 𝟐 𝒇 𝒚 𝒙, 𝒚 = −𝟐𝒚 𝒇 𝒙 𝒙, 𝒚 = −𝟐𝒙 Devidas parciais de 𝒇 𝒙, 𝒚 = 𝟗 − 𝒙 𝟐 − 𝒚 𝟐, no ponto (𝟏, −𝟏) Devidas parciais de 𝒇 𝒙, 𝒚 = 𝟗 − 𝒙 𝟐 − 𝒚 𝟐. O resultado é um número que representa a inclinação da reta tangente à 𝑓(𝑥, 𝑦) no ponto (1, −1). Veja que (1, −1) pertence ao domínio de 𝑓(𝑥, 𝑦) O resultado é uma função que representa a inclinação da reta tangente à 𝑓(𝑥, 𝑦) no ponto (𝑥, 𝑦) . Perceba que 𝑥, 𝑦 deve pertencer ao domínio de 𝑓(𝑥, 𝑦) Usaremos a definição apenas em algumas situações específicas. Na maioria das situações as derivadas parciais serão calculadas usando as regras de derivação já conhecidas do Cálculo I
- 18. Existem algumas notações alternativas para o operador derivadas parciais. Algumas mais econômicas em espaço e outras melhores para demonstrações Notação 𝒇 𝒙 𝟏, −𝟏 = 𝝏𝒇(𝟏, −𝟏) 𝝏𝒙 = 𝝏𝒛 𝝏𝒙 𝒙=𝟏 𝒚=−𝟏 = −𝟐 𝒇 𝒚 𝟏, −𝟏 = 𝝏𝒇(𝟏, −𝟏) 𝝏𝒚 = 𝝏𝒛 𝝏𝒚 𝒙=𝟏 𝒚=−𝟏 = 𝟐 𝒇 𝒚 𝒙, 𝒚 = 𝝏𝒇(𝒙, 𝒚) 𝝏𝒚 = 𝝏𝒛 𝝏𝒚 = −𝟐𝒚𝒇 𝒙 𝒙, 𝒚 = 𝝏𝒇(𝒙, 𝒚) 𝝏𝒙 = 𝝏𝒛 𝝏𝒙 = −𝟐𝒙 Devidas parciais de 𝒇 𝒙, 𝒚 = 𝟗 − 𝒙 𝟐 − 𝒚 𝟐, no ponto (𝟏, −𝟏) Devidas parciais de 𝒇 𝒙, 𝒚 = 𝟗 − 𝒙 𝟐 − 𝒚 𝟐. 𝒇 𝒙 𝒙, 𝒚 = 𝒇 𝒙 = 𝝏𝒇 𝝏𝒙 = 𝝏𝒇(𝒙, 𝒚) 𝝏𝒙 = 𝝏𝒛 𝝏𝒙 = 𝑫 𝒙 𝒇 = 𝐥𝐢𝐦 𝒉→𝟎 𝒇 𝒙 + 𝒉, 𝒚 − 𝒇 𝒙, 𝒚 𝒉 𝒇 𝒚 𝒙, 𝒚 = 𝒇 𝒚 = 𝝏𝒇 𝝏𝒚 = 𝝏𝒇(𝒙, 𝒚) 𝝏𝒚 = 𝝏𝒛 𝝏𝒚 = 𝑫 𝒚 𝒇 = 𝐥𝐢𝐦 𝒉→𝟎 𝒇 𝒙, 𝒚 + 𝒉 − 𝒇 𝒙, 𝒚 𝒉 Derivada com relação a 𝑦 mantendo 𝑥 como uma constante. Derivada com relação a 𝑥 mantendo 𝑦 como uma constante.
- 19. 3. Usando as regras de derivação, calcule as derivadas parciais de primeira ordem de 𝐳 = 𝒇 𝒙, 𝒚 = 𝟑𝒙 𝟒 𝒚 𝟓 . Exemplos 𝒇 𝒙 𝒙, 𝒚 = 𝝏 𝝏𝒙 𝟑𝒙 𝟒 𝒚 𝟓 = 𝟏𝟐𝒙 𝟑 𝒚 𝟓 Derivada com relação a 𝑥 mantendo 𝑦 como uma constante. Notação alternativ a. 𝒚 𝟓 𝝏 𝝏𝒙 𝟑𝒙 𝟒 = O 𝑦 é uma constante. Pode sair do operador Usando a regra do tombo, 𝟑 ⋅ 𝟒 = 𝟏𝟐 𝝏𝒛 𝝏𝒙 = 𝒇 𝒚 𝒙, 𝒚 = 𝝏 𝝏𝒚 𝟑𝒙 𝟒 𝒚 𝟓 = 𝟏𝟓𝒙 𝟒 𝒚 𝟒 Derivada com relação a 𝑦 mantendo 𝑥 como uma constante. Notação alternativ a. 𝒙 𝟒 𝝏 𝝏𝒚 𝟑𝒚 𝟓 = O 𝑥 é uma constante. Pode sair do operador Usando a regra do tombo, 𝟑 ⋅ 𝟓 = 𝟏𝟓 𝝏𝒛 𝝏𝒚 =
- 20. 3. Usando as regras de derivação, calcule as derivadas parciais de primeira ordem de 𝐳 = 𝒇 𝒙, 𝒚 = 𝐬𝐢𝐧(𝒙 𝟐 𝒚). Exemplos 𝝏 𝝏𝒙 sin(𝒙 𝟐 𝒚) = Derivada com relação a 𝑥 mantendo 𝑦 como uma constante. Usando a regra do tombo, fica 𝟐𝒙 Nota-se que 𝑓(𝑥, 𝑦) é uma função composta, do tipo sin(ℎ(𝑥, 𝑦)), onde ℎ 𝑥, 𝑦 = 𝑥2 𝑦. co𝑠 𝒙 𝟐 𝒚 ⋅ 𝝏 𝝏𝒙 𝒙 𝟐 𝒚 = Derivada de fora O 𝑦 é uma constante. Pode sair do operador co𝑠 𝒙 𝟐 𝒚 ⋅ 𝒚 ⋅ 𝝏 𝝏𝒙 𝒙 𝟐 = 𝟐𝒙𝒚 co𝑠 𝒙 𝟐 𝒚
- 21. 3. Usando as regras de derivação, calcule as derivadas parciais de primeira ordem de 𝐳 = 𝒇 𝒙, 𝒚 = 𝐬𝐢𝐧(𝒙 𝟐 𝒚). Exemplos 𝝏 𝝏𝒚 sin(𝒙 𝟐 𝒚) = Derivada com relação a y mantendo x como uma constante. Usando a regra do tombo, fica 1 Nota-se que 𝑓(𝑥, 𝑦) é uma função composta, do tipo sin(ℎ(𝑥, 𝑦)), onde ℎ 𝑥, 𝑦 = 𝑥2 𝑦. co𝑠 𝒙 𝟐 𝒚 ⋅ 𝝏 𝝏𝒚 𝒙 𝟐 𝒚 = Derivada de fora O 𝑥 é uma constante. Pode sair do operador co𝑠 𝒙 𝟐 𝒚 ⋅ 𝒙 𝟐 ⋅ 𝝏 𝝏𝒚 𝒚 = 𝒙 𝟐 co𝑠 𝒙 𝟐 𝒚 Derivada de fora Derivada de dentro
- 22. 4. Calcule as derivadas parciais de segunda ordem de 𝐳 = 𝒇 𝒙, 𝒚 = 𝐬𝐢𝐧(𝒙 𝟐 𝒚). Derivadas sucessivas Já temos o resultado das derivadas de primeira ordem . 𝝏 𝝏𝒚 sin(𝒙 𝟐 𝒚) = 𝒙 𝟐 co𝑠 𝒙 𝟐 𝒚 𝝏 𝟐 𝝏𝒙 𝟐 sin(𝒙 𝟐 𝒚) = 𝟐𝒙𝒚 co𝑠 𝒙 𝟐 𝒚 Vamos calcular, então, 𝝏 𝟐 𝝏𝒙 𝟐 sin(𝒙 𝟐 𝒚) e 𝝏 𝟐 𝝏𝒚 𝟐 sin(𝒙 𝟐 𝒚) . 𝝏 𝝏𝒙 sin(𝒙 𝟐 𝒚) = 𝝏 𝝏𝒙 𝟐𝒙𝒚 co𝑠 𝒙 𝟐 𝒚 = 𝝏 𝝏𝒙 𝟐𝒙𝒚 ⋅ co𝑠 𝒙 𝟐 𝒚 + 𝟐𝒙𝒚 ⋅ 𝝏 𝝏𝒙 co𝑠 𝒙 𝟐 𝒚 = 𝝏 𝝏𝒙 𝝏 𝝏𝒙 sin 𝒙 𝟐 𝒚 = 𝟐𝒚 co𝑠 𝒙 𝟐 𝒚 + 𝟐𝒙𝒚 − sin 𝒙 𝟐 𝒚 ⋅ 𝝏 𝝏𝒙 𝒙 𝟐 𝒚 = 𝟐𝒚 co𝑠 𝒙 𝟐 𝒚 − 𝟐𝒙𝒚 sin 𝒙 𝟐 𝒚 ⋅ 𝟐𝒙𝒚 = 𝟐𝒚 co𝑠 𝒙 𝟐 𝒚 − 𝟒𝒙 𝟐 𝒚 𝟐 sin 𝒙 𝟐 𝒚 Regra do produto Derivada da 1ª função 2ª função 1ª função Derivada da 2ª função Função composta
- 23. x é constante 4. Calcule as derivadas parciais de segunda ordem de 𝐳 = 𝒇 𝒙, 𝒚 = 𝐬𝐢𝐧(𝒙 𝟐 𝒚). Derivadas sucessivas Já temos o resultado das derivadas de primeira ordem . 𝝏 𝝏𝒚 sin(𝒙 𝟐 𝒚) = 𝒙 𝟐 co𝑠 𝒙 𝟐 𝒚 𝝏 𝟐 𝝏𝒚 𝟐 sin(𝒙 𝟐 𝒚) = 𝟐𝒙𝒚 co𝑠 𝒙 𝟐 𝒚 Vamos calcular, então, 𝝏 𝟐 𝝏𝒙 𝟐 sin(𝒙 𝟐 𝒚) e 𝝏 𝟐 𝝏𝒚 𝟐 sin(𝒙 𝟐 𝒚) . 𝝏 𝝏𝒙 sin(𝒙 𝟐 𝒚) = 𝝏 𝝏𝒚 𝒙 𝟐 co𝑠 𝒙 𝟐 𝒚 = 𝝏 𝝏𝒚 𝝏 𝝏𝒚 sin 𝒙 𝟐 𝒚 = Função composta 𝒙 𝟐 𝝏 𝝏𝒚 co𝑠 𝒙 𝟐 𝒚 = −𝒙 𝟐 sen 𝒙 𝟐 𝒚 𝝏 𝝏𝒚 𝒙 𝟐 𝒚 = x é constante −𝒙 𝟒 sen 𝒙 𝟐 𝒚 Derivada de fora Derivada de dentro
- 24. 5. Calcule as derivadas parciais mistas de ordem 2 da função 𝐳 = 𝒇 𝒙, 𝒚 = 𝐬𝐢𝐧(𝒙 𝟐 𝒚). Derivadas sucessivas Já temos o resultado das derivadas de primeira ordem . 𝝏 𝝏𝒚 sin(𝒙 𝟐 𝒚) = 𝒙 𝟐 co𝑠 𝒙 𝟐 𝒚𝟐𝒙𝒚 co𝑠 𝒙 𝟐 𝒚 𝝏 𝝏𝒙 sin(𝒙 𝟐 𝒚) = Vamos calcular, então, 𝝏 𝟐 𝝏𝒚𝝏𝒙 sin(𝒙 𝟐 𝒚) e 𝝏 𝟐 𝝏𝒙𝝏𝒚 sin(𝒙 𝟐 𝒚). 𝝏 𝟐 𝝏𝒚𝝏𝒙 sin(𝒙 𝟐 𝒚) = 𝝏 𝝏𝒚 𝟐𝒙𝒚 co𝑠 𝒙 𝟐 𝒚 = 𝝏 𝝏𝒚 𝝏 𝝏𝒙 sin 𝒙 𝟐 𝒚 = Regra do produto 𝝏 𝝏𝒚 𝟐𝒙𝒚 ⋅ co𝑠 𝒙 𝟐 𝒚 + 𝟐𝒙𝒚 ⋅ 𝝏 𝝏𝒚 co𝑠 𝒙 𝟐 𝒚 = 𝟐𝒙 co𝑠 𝒙 𝟐 𝒚 + 𝟐𝒙𝒚 − sin 𝒙 𝟐 𝒚 ⋅ 𝝏 𝝏𝒚 𝒙 𝟐 𝒚 = Regra do produto Derivada da 1ª função 2ª função 1ª função Derivada da 2ª função 𝟐𝒙 co𝑠 𝒙 𝟐 𝒚 − 𝟐𝒙𝒚 sin 𝒙 𝟐 𝒚 ⋅ 𝒙 𝟐 = 𝟐𝒙 co𝑠 𝒙 𝟐 𝒚 − 𝟐𝒙 𝟑 𝒚 sin 𝒙 𝟐 𝒚
- 25. 5. Calcule as derivadas parciais mistas de ordem 2 da função 𝐳 = 𝒇 𝒙, 𝒚 = 𝐬𝐢𝐧(𝒙 𝟐 𝒚). Derivadas sucessivas Já temos o resultado das derivadas de primeira ordem . 𝝏 𝝏𝒚 sin(𝒙 𝟐 𝒚) = 𝒙 𝟐 co𝑠 𝒙 𝟐 𝒚𝟐𝒙𝒚 co𝑠 𝒙 𝟐 𝒚 𝝏 𝝏𝒙 sin(𝒙 𝟐 𝒚) = Vamos calcular, então, 𝝏 𝟐 𝝏𝒚𝝏𝒙 sin(𝒙 𝟐 𝒚) e 𝝏 𝟐 𝝏𝒙𝝏𝒚 sin(𝒙 𝟐 𝒚). 𝝏 𝟐 𝝏𝒙𝝏𝒚 sin(𝒙 𝟐 𝒚) = 𝝏 𝝏𝒙 𝒙 𝟐 co𝑠 𝒙 𝟐 𝒚 = 𝝏 𝝏𝒙 𝝏 𝝏𝒚 sin 𝒙 𝟐 𝒚 = Regra do produto 𝝏 𝝏𝒙 𝒙 𝟐 ⋅ co𝑠 𝒙 𝟐 𝒚 + 𝒙 𝟐 ⋅ 𝝏 𝝏𝒙 co𝑠 𝒙 𝟐 𝒚 = 𝟐𝒙 co𝑠 𝒙 𝟐 𝒚 + 𝒙 𝟐 − sin 𝒙 𝟐 𝒚 ⋅ 𝝏 𝝏𝒙 𝒙 𝟐 𝒚 = Regra do produto Derivada da 1ª função 2ª função 1ª função Derivada da 2ª função 𝟐𝒙 co𝑠 𝒙 𝟐 𝒚 − 𝒙 𝟐 sin 𝒙 𝟐 𝒚 ⋅ 𝟐𝒙𝒚 = 𝟐𝒙 co𝑠 𝒙 𝟐 𝒚 − 𝟐𝒙 𝟑 𝒚 sin 𝒙 𝟐 𝒚 Mesmo resultado
- 26. Resumindo os exercícios 4, 5 e 6 Derivadas sucessivas Já temos o resultado das derivadas de primeira ordem . 𝝏 𝝏𝒚 sin(𝒙 𝟐 𝒚) = 𝒙 𝟐 co𝑠 𝒙 𝟐 𝒚𝟐𝒙𝒚 co𝑠 𝒙 𝟐 𝒚 𝝏 𝝏𝒙 sin(𝒙 𝟐 𝒚) = 𝝏 𝟐 𝒇(𝒙, 𝒚) 𝝏𝒙𝝏𝒚 = 𝝏 𝝏𝒙 𝒙 𝟐 co𝑠 𝒙 𝟐 𝒚 = 𝝏 𝝏𝒙 𝝏 𝝏𝒚 sin 𝒙 𝟐 𝒚 = 𝟐𝒙 co𝑠 𝒙 𝟐 𝒚 − 𝟐𝒙 𝟑 𝒚 sin 𝒙 𝟐 𝒚 𝝏 𝟐 𝒇(𝒙, 𝒚) 𝝏𝒚𝝏𝒙 = 𝝏 𝝏𝒚 𝟐𝒙𝒚 co𝑠 𝒙 𝟐 𝒚 = 𝝏 𝝏𝒚 𝝏 𝝏𝒙 sin 𝒙 𝟐 𝒚 = 𝟐𝒙 co𝑠 𝒙 𝟐 𝒚 − 𝟐𝒙 𝟑 𝒚 sin 𝒙 𝟐 𝒚 𝝏 𝟐 𝒇(𝒙, 𝒚) 𝝏𝒙 𝟐 = 𝝏 𝝏𝒙 𝟐𝒙𝒚 co𝑠 𝒙 𝟐 𝒚 = 𝝏 𝝏𝒙 𝝏 𝝏𝒙 sin 𝒙 𝟐 𝒚 = 𝟐𝒚 co𝑠 𝒙 𝟐 𝒚 − 𝟒𝒙 𝟐 𝒚 𝟐 sin 𝒙 𝟐 𝒚 𝝏 𝟐 𝒇(𝒙, 𝒚) 𝝏𝒚 𝟐 = 𝝏 𝝏𝒚 𝒙 𝟐 co𝑠 𝒙 𝟐 𝒚 = 𝝏 𝝏𝒚 𝝏 𝝏𝒚 sin 𝒙 𝟐 𝒚 = −𝒙 𝟒 sen 𝒙 𝟐 𝒚 Resultado Importante
- 27. Teorema de Clairaut Teorema de Clairaut Suponha que 𝑓(𝑥, 𝑦) seja definida em uma bola aberta 𝐷 que contenha o ponto (𝑎, 𝑏). Se as funções 𝝏 𝟐 𝒇(𝒙,𝒚) 𝝏𝒙𝝏𝒚 e 𝝏 𝟐 𝒇(𝒙,𝒚) 𝝏𝒚𝝏𝒙 forem ambas contínuas em 𝐷, então 𝝏 𝟐 𝒇(𝒙, 𝒚) 𝝏𝒙𝝏𝒚 = 𝝏 𝟐 𝒇(𝒙, 𝒚) 𝝏𝒚𝝏𝒙 𝑓 (𝑥, 𝑦) = 𝑥3 + 𝑥2 𝑦3 – 2𝑦2.Considere a função Analise as seguintes derivadas mistas: 𝝏𝒇(𝒙, 𝒚) 𝝏𝒙 = 3𝑥2 + 2𝑥𝑦3 𝝏 𝝏𝒙 𝑥3 + 𝑥2 𝑦3 – 2𝑦2 = 𝝏𝒇(𝒙, 𝒚) 𝝏𝒚 = 3𝑥2 𝑦2 – 4𝑦 𝝏 𝟐 𝒇(𝒙, 𝒚) 𝝏𝒙𝝏𝒚 = 𝝏 𝝏𝒙 𝝏𝒇 𝒙, 𝒚 𝝏𝒚 = 𝝏 𝝏𝒙 3𝑥2 𝑦2 – 4𝑦 = 6𝑥𝑦2 𝝏 𝟐 𝒇(𝒙, 𝒚) 𝝏𝒚𝝏𝒙 = 𝝏 𝝏𝒚 𝝏𝒇 𝒙, 𝒚 𝝏𝒙 = 𝝏 𝝏𝒚 3𝑥2 + 2𝑥𝑦3 = 6𝑥𝑦2 𝒚 se torna constante Mesmo resultado
- 28. Teorema de Clairaut Teorema de Clairaut Suponha que 𝑓(𝑥, 𝑦) seja definida em uma bola aberta 𝐷 que contenha o ponto (𝑎, 𝑏). Se as funções 𝝏 𝟐 𝒇(𝒙,𝒚) 𝝏𝒙𝝏𝒚 e 𝝏 𝟐 𝒇(𝒙,𝒚) 𝝏𝒚𝝏𝒙 forem ambas contínuas em 𝐷, então 𝝏 𝟐 𝒇(𝒙, 𝒚) 𝝏𝒙𝝏𝒚 = 𝝏 𝟐 𝒇(𝒙, 𝒚) 𝝏𝒚𝝏𝒙 Você também pode verificar que 𝝏 𝟑 𝒇(𝒙, 𝒚) 𝝏𝒙𝝏𝒚 𝟐 = 𝝏 𝟑 𝒇(𝒙, 𝒚) 𝝏𝒚 𝟐 𝝏𝒙 = 𝝏 𝟑 𝒇(𝒙, 𝒚) 𝝏𝒚𝝏𝒙𝝏𝒚 𝝏 𝝏𝒙 𝝏 𝝏𝒚 𝝏𝒇(𝒙, 𝒚) 𝝏𝒚 = 𝝏 𝝏𝒚 𝝏 𝝏𝒚 𝝏𝒇(𝒙, 𝒚) 𝝏𝒙 = 𝝏 𝝏𝒚 𝝏 𝝏𝒙 𝝏𝒇(𝒙, 𝒚) 𝝏𝒚 = 𝝏 𝟑 𝒇(𝒙, 𝒚) 𝝏𝒚𝝏𝒙 𝟐 = 𝝏 𝟑 𝒇(𝒙, 𝒚) 𝝏𝒙 𝟐 𝝏𝒚 = 𝝏 𝟑 𝒇(𝒙, 𝒚) 𝝏𝒙𝝏𝒚𝝏𝒙 𝝏 𝝏𝒚 𝝏 𝝏𝒙 𝝏𝒇(𝒙, 𝒚) 𝝏𝒙 = 𝝏 𝝏𝒙 𝝏 𝝏𝒙 𝝏𝒇(𝒙, 𝒚) 𝝏𝒚 = 𝝏 𝝏𝒙 𝝏 𝝏𝒚 𝝏𝒇(𝒙, 𝒚) 𝝏𝒙 = E ainda verificar que
- 29. Anote suas dúvidas! Estarei sempre disposto a tirar vossas dúvidas. Boa leitura!