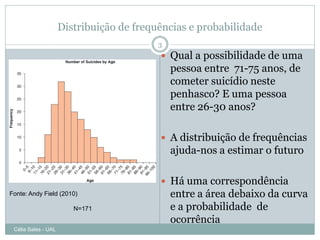
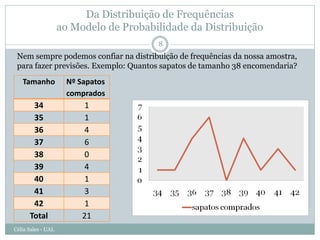
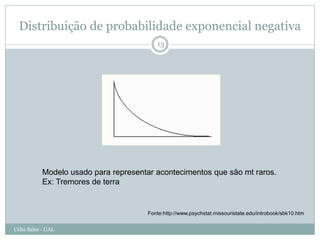
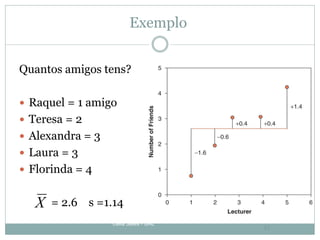
O documento discute distribuições de probabilidade, incluindo a curva normal e z-scores. Aborda conceitos como modelos de distribuição, parâmetros, áreas sob a curva, e como z-scores podem ser usados para padronizar dados e consultar tabelas de probabilidade.

1. Distribuição de Probabilidade, Curva Normal, Z-Scores
PROFª DOUTORA CÉLIA SALES

2. Conteúdos
2
 Da distribuição de frequências ao modelo de
distribuição
 Modelos de Probabilidade
 Definição
 Exemplos
 Distribuição Normal
 Distribuição Normal estandardizada
 Z-scores
Célia Sales - UAL

3. Distribuição de frequências e probabilidade
3
 Qual a possibilidade de uma
pessoa entre 71-75 anos, de
cometer suicídio neste
penhasco? E uma pessoa
entre 26-30 anos?
 A distribuição de frequências
ajuda-nos a estimar o futuro
 Há uma correspondência
Fonte: Andy Field (2010) entre a área debaixo da curva
N=171 e a probabilidade de
ocorrência
Célia Sales - UAL

4. Probabilidade
4
Fortuna Imperatrix Mundi
Sem a capacidade de tomar decisões em situação de
incerteza, guiado pela avaliação das
probabilidades, um animal fraco como o homem
estaria decerto extinto em vez de se ter tornado a
praga de maior sucesso no planeta.
(Pestana & Velosa, 2006, p. 191)
Célia Sales - UAL

5. Probabilidade
5
A probabilidade é um termo primitivo, medindo o
grau de possibilidade de um acontecimento
incerto se realizar
(Pestana & Velosa, 2006, p. 192)
Célia Sales - UAL

6. 6
Publica em 1812, o
livro
THÉORIE
ANALYTIQUE DES
PROBABILITÉS
onde enuncia os
princípios gerais que
devem guiar a
atribuição e cálculo
de probabilidades
Pierre-Simon Laplace (1794-1827)
Célia Sales - UAL

7. Probabilidade Laplaciana
7
 A probabilidade de um acontecimento A
Se os casos possíveis tiverem a mesma probabilidade
de acontecerem (equiprováveis)
Célia Sales - UAL

8. Da Distribuição de Frequências
ao Modelo de Probabilidade da Distribuição
8
Nem sempre podemos confiar na distribuição de frequências da nossa amostra,
para fazer previsões. Exemplo: Quantos sapatos de tamanho 38 encomendaria?
Tamanho Nº Sapatos
comprados
34 1
35 1
36 4
37 6
38 0
39 4
40 1
41 3
42 1
Total 21
Célia Sales - UAL

9. Distribuição de Frequências
e Modelos de Probabilidade
9
 No exemplo dos sapatos, a distribuição de frequência não é
um bom critério para planear a quantidade de sapatos a
encomendar
 Pelo facto de, na amostra (N=21), não ter aparecido ninguém a calçar
o 38, não quer dizer que não seja necessário ter esse nº em stock…
 Sabemos que, noutra amostra, possivelmente haveria alguém a
calçar o 38 (principalmente se a amostra fosse maior)
 Modelo de Probabilidade
 Como seria a curva de distribuição de frequências do tamanho de
sapato, se medíssemos um nº infinito de pés de mulheres adultas?
 Esse modelo (ou curva de distribuição “ideal”) seria uma alternativa
melhor do que a distribuição de frequências da amostra, para
estimar o tamanho de sapatos a encomendar
Célia Sales - UAL

10. Distribuição de probabilidade. Definição.
10
 Modelo de distribuição de frequência = Distribuição de
probabilidade = Modelo de Probabilidade
 Curva que descreve uma distribuição de frequências
idealizada (ou teórica) de uma certa variável
 A distribuição é idealizada porque corresponde à
distribuição de frequências que obteríamos se tivessemos
um número infinito de resultados
 A partir dessa curva é possível calcular a probabilidade
de ocorrência de valores específicos da variável
 Expressão algébrica que descreve a frequência relativa (a
curva) de todos os valores possíveis
Célia Sales - UAL

11. Modelos de Probabilidade. Exemplos
11
 Exemplos:
1. Distribuição Uniforme ou Rectangular
2. Distribuição Exponencial Negativa
3. Distribuição Normal ou Curva Normal
Célia Sales - UAL

12. Distribuição de probabilidade uniforme
12
Cada resultado tem a mesma probabilidade de acontecer.
Fonte:http://www.psychstat.missouristate.edu/introbook/sbk10.htm
Célia Sales - UAL

13. Distribuição de probabilidade exponencial negativa
13
Modelo usado para representar acontecimentos que são mt raros.
Ex: Tremores de terra
Fonte:http://www.psychstat.missouristate.edu/introbook/sbk10.htm
Célia Sales - UAL

14. Distribuição Normal
14
Distribuição de probabilidade de uma variável aleatória,
que é perfeitamente simétrica (achatamento=0 e assimetria
=0) (Field, 2010)
 A maior parte das variáveis sociais e psicológicas seguem um
distribuição Normal
Fonte:http://www.psychstat.missouristate.edu/introbook/sbk10.htm
Célia Sales - UAL

15. Propriedades das Distribuições de Probabilidade
15
1. Parâmetros
(presentes em quase todos os modelos de probabildiade).
Parâmetros são variáveis do modelo que têm que ser
estabelecidas à partida; mudando os parâmetros de um
modelo de probabilidade muda a forma da curva
2. A área total debaixo da curva é igual a 1
Pelo mesmo motivo pelo qual a soma total da distribuição de
frequências relativas numa amostra tem que ser 1 (ou 100%)
3. A área debaixo da curva, entre dois resultados
quaisquer é uma PROBABILIDADE
Probabilidade de um acontecimento = Frequência relativa
teórica desse acontecimento num modelo da população.
Célia Sales - UAL

16. Curva Normal
16
Constantes: Variáveis:
π = 3,1416… X - valor do resultado
e = 2,81… µ Parâmetros
σ
Célia Sales - UAL

17. Distribuição de probabilidades. Utilidade:
17
 Os estatísticos identificaram várias distribuições
presentes muitas vezes na realidade
 Para algumas dessas distribuições, desenvolveram uma
fórmula que especifica versões idealizadas (teóricas)
dessas distribuições (isto é, a distribuição de
probabilidade), que corresponde a uma curva
 Se certa variável tiver uma distribuição semelhante a
uma destas distribuição de probabilidade (ex: Distrib.
Normal), podemos calcular a probabilidade de
ocorrência de valores específicos
 Essa probabilidade é dada pela área, debaixo da curva, entre
dois valores
Célia Sales - UAL

18. Tabela de probabilidade da distribuição de normal
18
 Os estatísticos calcularam a probabilidade de certos valores
ocorrerem numa distribuição normal com uma média de 0
(zero) e desvio padrão 1
 Colocaram estes valores numa tabela: Tabela de probabilidade da
distribuição normal
Assim:
 Se tivermos dados que se distribuem com uma forma normal
 Se a média dessa distribuição for zero e o desvio padrão for 1,
 Podemos consultar a tabela e ver qual a probabilidade de um
certo Resultado acontecer
Célia Sales - UAL

19. Temos apenas um pequeno problema…
19
Nem todos os dados com distribuição em forma
normal têm média=0 e DP=1…
Se conseguíssemos esta transformação poderíamos
usar as tabelas de distribuição da probabilidade
Z-scores
Célia Sales - UAL

20. Lógica dos Z-scores
20
Calcular o desvio em
X X
relação à média (“centrar”)
z
s Usar o desvio-padrão como
unidade de medida
(“reduzir”)
(como se fossem dúzias… 24 ovos a
dividir por 12, passam a 2 dúzias –
unidade de medida passa a dúzias)
Célia Sales - UAL

21. Exemplo
Quantos amigos tens?
 Raquel = 1 amigo
 Teresa = 2
 Alexandra = 3
 Laura = 3
 Florinda = 4
X = 2.6 s =1.14
Célia Sales - UAL
21

22. scores v.s z-scores
22
Scores Z-scores
média = 2.6 e s = 1.14 Média = 0 e s = 1
Os resultados (scores) são: Os “z-scores” são:
1 amigo
2 amigos 1  2.6
3 amigos   1.40 Desvios em
1.14 relação à média
3 amigos
4 amigos 2  2.6
etc ...
1.14
Resultados estandardizados
Resultados observados
(Resultado observado
expresso em unidades de desvio padrão)
Célia Sales - UAL

23. Exemplo do penhasco
23
Qual é a probabilidade de uma pessoa de 70 anos ou
mais se suicidar no Penhasco?
(Partindo do pressuposto de que esta distribuição tem uma forma
normal…)
1º passo
Converter 70 em z-score
(média de suicídios = 36; desvio padrão = 13)
2º passo
Procurar o valor obtido na tabela da distribuição
normal estandardizada Coluna “SMALLER PART”
Célia Sales - UAL

24. Compreendemos então que…
24
A distribuição normal estandardizada permite-nos:
 Partir de um conjunto de resultados para calcular a
probabilidade de ocorrência de um certo resultado
 Saber se um certo resultado pode ou não acontecer
numa certa distribuição
 Esta noção está na base da lógica do cálculo de p, nos testes de
hipóteses
Célia Sales - UAL

25. Dados importantes sobre a distribuição normal
25
 68% dos valores situam-se entre + ou – 1 desvio
padrão da média
 95% dos valores situa-se entre + ou – 2 desvios
padrões da média
 99.7% situam-se entre + ou – 3 desvios padrões da
média
Célia Sales - UAL

26. Leitura de apoio:
26
 http://www.psychstat.missouristate.edu/introbook/
sbk10.htm
 Muito recomendado para compreender o conceito de
Distribuição de Probabilidade
 Tem exemplos interactivos de simulação da Curva Normal
 Field (2010), cap. 1
Célia Sales - UAL