Este documento apresenta um resumo do capítulo 1 - Limites do curso de Cálculo ministrado pelo professor Gustavo Viegas. O capítulo introduz os conceitos fundamentais de limites, incluindo limites num ponto, limites laterais, limites infinitos e assíntotas verticais, ilustrando cada tópico com exemplos.

1. Versão 1
Março de 2016 Curso de Cálculo
Prof. Gustavo Viegas

2. todaamatematica.com pág 1 engenhariae.com.br
Índice
Capítulo 1 - Limites
Limite num ponto Pág. 3
Limites infinitos Pág. 5
Operações com limites Pág. 7
Limites no infinito Pág. 9
Alguns limites no infinito Pág. 10
Indeterminação 0/0 Pág. 12
Funções contínuas Pág. 13
Teorema do valor intermediário Pág. 16
Continuidade das funções trigonométricas Pág. 17
Teorema do confronto Pág. 19
Limites trigonométricas Pág. 21

3. todaamatematica.com pág 2 engenhariae.com.br
Este livro é o material para acompanhar o
Curso de Cálculo disponível no canal do
Youtube do Toda a Matemática.
www.youtube.com/cursogustavoviegas
Para um estudo mais completo, temos
o nosso curso presencial.
Apoio:
engenhariae.com.br

4. todaamatematica.com pág 3 engenhariae.com.br
TODA A MATEMÁTICA
GUSTAVO VIEGAS
LIMITES
CURSO PRESENCIAL:
Av. Osvaldo Aranha 734/404
Porto Alegre - RS
CURSO DE CÁLCULO CAPÍTULO 1
LIMITE NUM PONTO
Problema da reta tangente
Dada uma função 𝑓 e um ponto em seu gráfico, encontrar a
equação da reta tangente ao gráfico de 𝑓 naquele ponto.
Problema da área
Dada uma função 𝑓, encontrar a área entre o gráfico de 𝑓 e
um intervalo [a, b] no eixo x.
Em 1665, Newton e, onze anos mais tarde, Leibniz
conseguiram entender que o problema da reta tangente e o
problema da área estão relacionados e foram os primeiros a
desenvolver técnicas gerais para resolvê-los.
O primeiro problema está relacionado às derivadas e o
segundo às integrais e ambos envolvem um processo de
limite. Esse foi o desenvolvimento inicial do Cálculo
Diferencial e Integral.
Isaac Newton
(1643 - 1727)
Gottfried Leibniz
(1646 - 1726)
Mais tarde, principalmente com D´Alembert, notou-se que
tanto o processo de derivação quanto o de integração
precisavam ser postos em bases mais sólidas e isso
dependia, inicialmente, de um estudo mais completo de
limites. Cauchy chegou perto de resolver o problema, mas
foi só em 1850 que Weierstrass desenvolveu os limites com
precisão.
Jean D´Alembert
(1717 – 1783)
Augustin Cauchy
(1789 – 1857)
Exemplo 1
E1(1,8 ; 0,50)
E2(1,9 ; 0,70)
E3(1,99 ; 0,85)
E4(1,995 ; 0,98)
D1(2,4 ; 1,3)
D2(2,2 ; 1,12)
D3 (2,1 ; 1,03)
D4(2,01 ; 1,004)
Quando x está cada vez mais perto de 2, as imagens 𝑓(x)
ficam cada vez mais próximas de y = 1, e isso acontece
tanto à esquerda, quando à direita, dizemos que o limite de
𝑓 quando x tende a 2 é 1. Escrevemos
lim
x  2
𝑓(x) = 1
Observação
É importante notar que o limite num ponto não tem relação
com o valor da função ali.
Notação
Weierstrass inventou a abreviação lim, mas em 1908 Hardy
escreveu a notação atual para limites, lim
x  a
𝑓(x).
Weierstrass
(1815 -1897)
Godfrey Hardy
(1877 - 1847)
Limite num ponto (informalmente)
O limite da função 𝑓 em x = a é L, lim
x  a
𝑓(x) = L, se os
valores de 𝑓(x) puderem ser tomados tão próximos de L
quanto se queira, desde que sejam tomados valores de x
suficientemente próximos de a (mas não iguais a).

5. todaamatematica.com pág 4 engenhariae.com.br
Exemplo 2
E1(2,6 ; 1,002)
E2(2,8 ; 1,04)
E3(2,9 ; 1,1)
D1(3,5 ; 2,9)
D2(3,3 ; 3,012)
D3(3,1 ; 3,002)
Quando x se aproxima de 3, pelo lado esquerdo, as imagens
𝑓(x) ficam cada vez mais próximas de y = 1. Dizemos que o
limite de 𝑓 quando x tende a 3 pela esquerda é 1 e
escrevemos lim
x  3−
𝑓(x) = 1.
Analogamente, pela direita, lim
x  3+
𝑓(x) = 3.
Observação
Os limites laterais não têm relação com o valor da função ali.
Limite lateral pela esquerda
O limite da função 𝑓 em x = a pela esquerda é L,
lim
x  a−
𝑓(x) = L, se os valores de 𝑓(x) puderem ser tomados
tão próximos de L quanto se queira, desde que sejam
tomados valores de x suficientemente próximos de a (mas
menores do que a).
Analogamente, temos o limite pela direita, lim
x  a+
𝑓(x) = L.
Limite bilateral
lim
x  a
𝑓(x) = L se, e somente se, lim
x  a−
𝑓(x) = L = lim
x  a+
𝑓(x)
Observação
lim
x  2−
𝑓(x) = 1
lim
x  2+
𝑓(x) = 1
lim
x  2
𝑓(x) = 1
lim
x  3−
𝑓(x) = 1
lim
x  3+
𝑓(x) = 3
lim
x  3
𝑓(x) não existe
Exemplo 3
Calculando tanto pela esquerda quanto pela direita, temos
uma ideia de que o limite da função 𝑓 em
x = 1 é 2. Isso se confirma verificando no gráfico.
lim
x  1−
x − 1
√x − 1
𝐱 𝒇(𝐱)
𝟎, 𝟗𝟗𝟗 1,9995
𝟎, 𝟗𝟗𝟗𝟗 1,99995
𝟎, 𝟗𝟗𝟗𝟗𝟗 1,999995
lim
x  1+
x − 1
√x − 1
𝐱 𝒇(𝐱)
𝟏, 𝟎𝟏 2,004988
𝟏, 𝟎𝟎𝟏 2,005
𝟏, 𝟎𝟎𝟎𝟏 2,00005
lim
x  1
x − 1
√x − 1
= 2
Exemplo 4
Calculando tanto pela esquerda quanto pela direita, temos
uma ideia de que o limite da função 𝑓 em
x = 0 é 0, mas isso está errado. Aconteceu que fizemos uma
escolha muito ruim dos pontos, o que levou à conclusão
errada. O limite da função naquele ponto não existe.
Isso mostra que precisaremos de técnicas para o cálculo de
limites, não podendo simplesmente ficar substituindo
valores e estimando qual o resultado final.
lim
x 0−
sen (
π
x
)
𝐱 𝒇(𝐱)
−𝟎, 𝟏 0
−𝟎, 𝟎𝟏 0
−𝟎, 𝟎𝟎𝟏 0
lim
x 0+
sen (
π
x
)
𝐱 𝒇(𝐱)
𝟎, 𝟏 0
𝟎, 𝟎𝟏 0
𝟎, 𝟎𝟎𝟏 0
lim
x 0
sen (
π
x
)
Não existe.
Se você escolher um valor qualquer L no intervalo [−1 ; 1],
é possível escolher infinitos pontos com abscissa cada vez
mais próxima de x = 0 de maneira que as imagens valem
sempre L.

6. todaamatematica.com pág 5 engenhariae.com.br
LIMITES INFINITOS
Exemplo 1
𝑓(x) =
1
x
E1(−0,25 ; −4)
E2(−0,1 ; −10)
E3(−0,02 ; − 50)
E4(−0,01 ; −100)
D1(0,25 ; 4)
D2(0,1 ; 10)
D3(0,02 ; 50)
D4(0,01 ; 100)
Quando x está cada vez mais perto de 0 pela esquerda, as
imagens 𝑓(x) decrescem sem cota. Dizemos que
lim
x  0−
1
x
= −∞
Analogamente,
lim
x  0+
1
x
= +∞
Limites infinitos (informalmente)
lim
x  a−
𝑓(x) = +∞
lim
x  a+
𝑓(x) = +∞
significam que 𝑓(x) crescem sem cota quando x tende a a
pela esquerda ou pela direita, respectivamente. Quando
valem os dois limites infinitos, dizemos que
lim
x  a
𝑓(x) = +∞
Analogamente com,
lim
x  a−
𝑓(x) = −∞
lim
x  a+
𝑓(x) = −∞
Observação
Em 1665, Wallis adotou o
símbolo  para representar o
infinito.
John Wallis
(1616 - 1703)
Observação
𝑓(x) =
1
xn
n par
𝑓(x) =
1
xn
n ímpar
Exemplo 2
lim
x  1−
1
(x − 1)2
= +
lim
x  1+
1
(x − 1)2
= +
lim
x  1
1
(x − 1)2
= +
lim
x  1−
−
1
x − 1
= +
lim
x  1+
−
1
x − 1
= −
lim
x  1
−
1
x−1
não existe
Exemplo 3
Conforme as abscissas aproximam-se x = −2 , os pontos do
gráfico da função ficam cada vez mais próximos da reta
vertical de x = −2. Dizemos que essa é uma assíntota
vertical do gráfico.

7. todaamatematica.com pág 6 engenhariae.com.br
Assíntotas verticais
Uma reta x = a é uma assíntota vertical se vale algum dos
limites:
lim
x  a−
𝑓(x) = −∞
lim
x  a+
𝑓(x) = −∞
lim
x  a+
𝑓(x) = +∞
lim
x  a+
𝑓(x) = −∞
A palavra assíntota vem do grego assymptotos, que significa
“que não pode coincidir”.
Exemplo 4
A reta x = 1 é
assíntota vertical.
A reta x = 0 é
assíntota vertical
da função y = ln x
x = 1 é assíntota
vertical, mesmo
que o limite pela
direita seja finito.
A função y = tan x
possui infinitas
assíntotas
verticais.
Exemplo 5
lim
x  6
x2
x − 6
A substituição de x = 6 na expressão nos leva a uma
indeterminação
36
0
. Em casos assim, calculamos os limites
laterais.
𝐱 𝒇(𝐱)
𝟓, 𝟗 −348,1
𝟓, 𝟗𝟗 −3588,01
𝟓, 𝟗𝟗𝟗 −35988,001
lim
x  6−
x2
x − 6
= −∞
Temos uma maneira mais prática de calcular isso. Basta
notar que para valores próximos a x = 6 pela esquerda
encontramos
36
−0
Pela direita, segue a mesma ideia
𝐱 𝒇(𝐱)
𝟔, 𝟏 372,1
𝟔, 𝟎𝟏 3612,01
𝟔, 𝟎𝟎𝟏 36012,001
lim
x  6+
x2
x − 6
= +∞
É mais simples notar que para valores próximos a x = 6 pela
direita encontramos
36
+0
lim
x  6−
x2
x − 6
= −∞
lim
x  6+
x2
x − 6
= +∞
lim
x  6
x2
x−6
não existe
Exemplo 6
Para encontrar a assíntota vertical de
y =
1 − x
x + 2
vamos calcular o limite no valor que anula o
denominador, ou seja, x = −2.
lim
x  −2
1 − x
x + 2

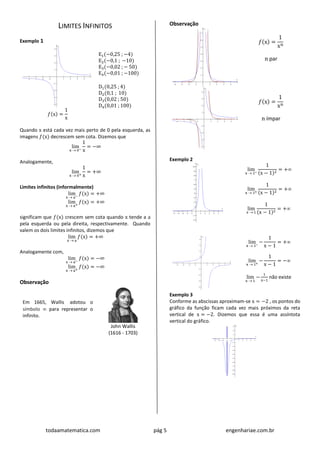
8. todaamatematica.com pág 7 engenhariae.com.br
A substituição de x = 2 na expressão nos leva a uma
indeterminação
3
0
. Informalmente, substituímos um valor à
esquerda (digamos x = −2,001) e encontramos.
3
−0
Pela direita, digamos x = −1,999) e encontramos.
3
+0
lim
x  −2−
1 − x
x + 2
= −∞
lim
x  −2+
1 − x
x + 2
= +∞
lim
x  −2
1−x
x+2
não
existe
Exemplo 7
lim
x  1
x
(x − 1)2
A substituição de x = 1 na expressão nos leva a uma
indeterminação
1
0
. Informalmente, substituímos um valor à
esquerda (digamos x = 0,999) e encontramos.
1
+0
Pela direita, digamos x = 1,001) e encontramos.
1
+0
lim
x  1−
x
(x − 1)2
= +∞
lim
x  1+
x
(x − 1)2
= +∞
lim
x  1
x
(x − 1)2
= +∞
OPERAÇÕES COM LIMITES
Limites fundamentais
Na função identidade y = x, conforme formos tomando
pontos cada vez mais próximos de x = a, teremos imagens
cada vez mais próximas desse mesmo valor, ou seja,
lim
x  a
x = a
Na função constante y = c, as imagens valem sempre o
valor, ou seja,
lim
x  a
c = c
Exemplo 1
lim
x  2
x = 2
lim
x  3
7 = 7
Definição de limite num ponto
Nesse momento, não queremos discutir o que é,
rigorosamente, o limite
lim
x  a
𝑓(x) = L
Como uma breve apresentação, Weierstrass definiu assim:
para todo  > 0, existe  > 0 tal que se 0 < |x − a| < , então
|𝑓(x) − L| < .
Operações com limites
Sejam
lim
x  a
𝑓(x) = L1
lim
x  a
𝑔(x) = L2
A partir da definição, conseguimos provar que
lim
x  a
[𝑓(x) ± 𝑔(x)] = L1 ± L2
lim
x  a
𝑓(x)𝑔(x) = L1L2
lim
x  a
𝑓(x)
𝑔(x)
=
L1
L2
, L2 0

9. todaamatematica.com pág 8 engenhariae.com.br
Observação
Se 𝑓(x) = c e lim
x  a
𝑔(x) = L
lim
x  a
𝑓(x)𝑔(x) = lim
x  a
c lim
x  a
𝑔(x) = c lim
x  a
𝑔(x) = cL
Isso significa que as constantes passam para fora do limite.
Exemplo 2
lim
x  1
2 + 3x + x2
= lim
x  1
2 + lim 3x
x  1
+ lim
x  1
x2
lim
x  1
2 + 3 lim x
x  1
+ ( lim
x  1
x) ( lim
x  1
x)
= 2 + 3.1 + 1.1 = 6
Limite de um polinômio
Diretamente das operações com limites, encontramos que
para 𝑝(x) = a0 + a1x + ⋯ + anxn
,
lim
x  a
𝑝(x) = 𝑝(a)
Exemplo 3
lim
x  1
2 + 3x + x2
= 2 + 3.1 + 12
= 6
Limite de uma função racional
Uma função racional é o quociente de dois polinômios
𝑓(x) =
a0 + a1x + ⋯ + anxn
c0 + c1x + ⋯ + cnxn
Se os limites do numerador p e denominador q existirem,
então
lim
x  a
p(x)
q(x)
=
L1
L2
, L2 0
Exemplo 4
lim
x  3
x + 1
x2 + 3x + 2
=
3 + 1
32 + 3.3 + 2
=
4
20
=
1
5
Exemplo 5
lim
x  −1
x + 1
x2 + 3x + 2
=
−1 + 1
(−1)2 + 3(−1) + 2
=
0
0
Temos uma aula para as indeterminações desse tipo.
Exemplo 6
lim
x  −2
x + 1
x + 2
=
−1
0
Com isso, devemos analisar os limites laterais.
lim
x  −2−
x + 1
x + 2
= +∞
lim
x  −2+
x + 1
x + 2
= −∞
Assim, o limite não existe.
Observação
lim
x  0+
(
1
x
−
1
x2
) = lim
x  0+
1
x
− lim
x  0+
1
x2
= ∞ − ∞
Não podemos separar o limite da diferença quando não
forem números reais. É necessário rescrever
lim
x  0+
(
1
x
−
1
x2
) = lim
x  0+
lim
x  0+
x − 1
x2
= −∞
Proposição
Se lim
x  a
𝑓(x) = 0 e 𝑔 é uma função limitada, então
lim
x  a
𝑓(x)𝑔(x) = 0
Exemplo 7
lim
x  0
xsen (
1
x
) = 0
pois lim
x  0
x = 0 e g(x) = sen (
1
x
) é uma função limitada.
|sen (
1
x
)|  1
y = xsen (
1
x
)

10. todaamatematica.com pág 9 engenhariae.com.br
LIMITES NO INFINITO
Quando os valores de x crescem sem parar, escrevemos
x  + . Quando decrescem sem parar, x  − .
Limites fundamentais
𝑓(x) =
1
x
E1(−10 ; −0,1)
E2(−100 ; −0,01)
E3(−1000 ; −0,001)
D1(10 ; 0,1)
D2(100 ; 0,01)
D3(1000 ; 0,001)
Quando x cresce cada vez mais, as imagens 𝑓(x) tendem a
zero. Dizemos que
lim
1
x
x  +
= 0
Analogamente,
lim
1
x
x  −
= 0
Limites no infinito (informalmente)
lim 𝑓(x)
x  +
= L significa que que os valores de 𝑓(x) ficam tão
próximos quanto quisermos de um número L à medida que
x cresce sem parar.
Analogamente com lim 𝑓(x)
x  −
= L.
Exemplo 1
Conforme x cresce sem parar, os pontos do gráfico da
função ficam cada vez mais próximos da reta horizontal y =
3. Dizemos que essa é uma assíntota horizontal do gráfico.
Assíntota horizontal
Uma reta y = L é uma assíntota horizontal se vale algum dos
limites:
lim 𝑓(x)
x  +
= L
lim 𝑓(x)
x  −
= L
Exemplo 2
y = sen(x) não tem
assíntotas horizontais.
y = arctan(x)
tem assíntota
y =
π
2
e y = −
π
2
𝑓(x) = (1 +
1
x
)
x
tem assíntota y = e.
𝑓(x) =
sen(x)
x
tem assíntota y = 0.
A função y = C tem
assíntota em y = C.
Observação
O precursor da ideia de limite no
infinito é Mādhava.
Mādhava de
Sangamagrama
(1350 - 1425
Exemplo 3
lim
x  +
ex
= +∞
lim
x  −
ex
= 0

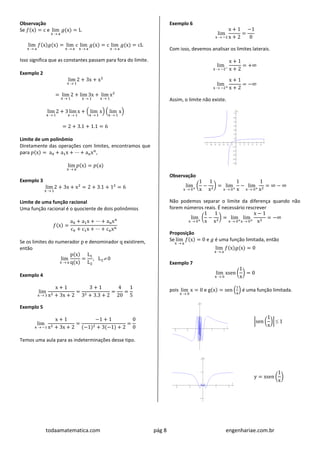
11. todaamatematica.com pág 10 engenhariae.com.br
lim
x  +
e−x
= 0
lim
x  −
e−x
= +∞
lim
x  +
ln(x) = +∞
lim
x  0+
ln(x) = −∞
Limites infinitos no infinito (informalmente)
Se os valores de 𝑓(x) crescem sem cota quando x  + ,
dizemos que
lim
x  +
𝑓(x) = +∞
Analogamente, lim
x  −
𝑓(x) = +∞
lim
x  +
𝑓(x) = −∞
lim
x  −
𝑓(x) = −∞
Exemplo 4
a) lim
x  0+
e1/x
= +∞
b) lim
x  0−
e1/x
= 0
Exemplo 5
Este é um modelo para o número de milhões de habitantes
nos EUA, em que o tempo é contado a partir de 1950. Qual
a expectativa de habitantes para daqui muito tempo?
p(t) =
50371,7
151,3 + 181,626 e−0,031636(t−1950)
lim
t + ∞
p(t) =
50371,7
151,3 + 0
= 333
Exemplo 6
a) lim
x  1−
ln(1 − x) = −∞
b)
lim
x  +∞
ln (
1
x
) = −∞
Exemplo 7
lim
x  +∞
[ln(x2
− 1) − ln(x + 1)]
= lim
x  +∞
ln
(x2
− 1)
x + 1
= lim
x  +∞
ln
(x + 1)(x − 1)
x + 1
= lim
x  +∞
ln(x − 1) = +∞
ALGUNS LIMITES NO INFINITO
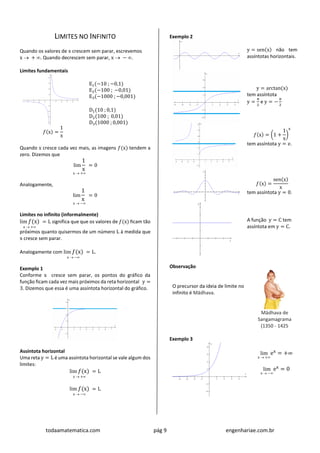
Observação
É importante conhecer o formato dos seguintes gráficos,
principalmente no que se refere ao seu comportamento
para valores muito grandes ou muito pequenos de x .
y = xn
n par
y = xn
n ímpar
n par
lim
x  +
xn
= +∞
lim
x  −
xn
= +∞
n ímpar
lim
x  +
xn
= +∞
lim
x  −
xn
= −∞
Exemplo 1
lim
x  +
(x3
+ 4x − 2)
= lim
x  +
x3
(1 +
4
x2
−
2
x3
)
= lim
x  +
x3
= +∞
Limites no infinito de polinômios
anxn
+ . . . + a1x + a0 = xn
(an + ⋯ +
a1
xn−1
+
a0
xn
)
lim
x ± 
(anxn
+ ⋯ + a1x + a0) = lim
x  ±
anxn
Exemplo 2
lim
x  +
(−x4
+ 4x3
− 2x)
= lim
x  +
(−x4)
= − lim
x  +
x4
= −∞

12. todaamatematica.com pág 11 engenhariae.com.br
Exemplo 3
Para limites de funções racionais, dividimos o numerador e
o denominador pela maior potência de x que aparece no
denominador.
lim
x  +
3x4
− 1
5x − 1
= lim
x  +
3x4
− 1
x
5x − 1
x
= lim
x  +
3x3
−
1
x
5 −
1
x
= lim
x  +
3x3
5
= +∞
Limites no infinito de funções racionais
Mais prático do que dividir pela maior potência de x que
aparece no denominador é observar que estamos
trabalhando com polinômios e seu comportamento no final
da função é governado pelo termo de maior grau.
lim
x  ±
anxn
+ ⋯ + a1x + a0
bmxm + ⋯ + b1x + b0
= lim
x  ±
anxn
bmxm
Exemplo 4
lim
x  +
(
3x4
− 1
5x − 1
) = lim
x  +
(
3x4
5x
) = lim
x  +
3
5
x3
= +
Exemplo 5
lim
x  +
(
−x5
+ x3
5x5 − 2x
) = lim
x  +
(
−x5
5x5
) = lim
x  +
(
−1
5
) = −
1
5
Exemplo 6
lim
x  +
(
2x3
+ 3
3x5 + 2x + 3
) = lim
x  + 
(
2x3
3x5
) = lim
x + 
2
3x2
= 0
Observação
√x2 = |x| = {
x, se x  0
−x, se x < 0
Exemplo 7
lim
x  +
√3x2 − 1
2x − 4
= lim
x  +
√3x2 − 1
|x|
2x − 4
|x|
Como x  + , então o valor é positivo e |x| = x.
= lim
x  +
√3x2 − 1
√x2
2x − 4
x
= lim
x  +
√3x2 − 1
x2
2 −
4
x
= lim
x  +
√3 −
1
x2
2 −
4
x
=
√3
2
Ou ainda
lim
x  +
√3x2
2x
= lim
x  +
√3√x2
2x
= lim
x  +
√3|x|
2x
= lim
x  +
√3x
2x
=
√3
2
Exemplo 8
lim
x  +
(√x2 − 1 − x)
Para limites assim, usamos (a − b)(a + b) = a2
− b2
.
= lim
x  +
(√x2 − 1 − x)(√x2 − 1 + x)
(√x2 − 1 + x)
= lim
x  +
(x2
− 1) − x2
(√x2 − 1 + x)
= lim
x  +
−1
(√x2 − 1 + x)
= 0

13. todaamatematica.com pág 12 engenhariae.com.br
INDETERMINAÇÃO 0/0
A técnica mais simples para resolver uma indeterminação
0/0 é usar a regra de L´Hopital. Todavia, isso envolve
derivadas. Enquanto não temos esse conhecimento,
precisaremos de algumas manipulações algébricas.
Observação
A simples retirada do ponto não altera o limite da função ali.
Esta será nossa ideia para resolver as indeterminações do
tipo 0/0: encontrar uma função mais simples com mesmo
limite no ponto considerado.
y = x − 2
lim
x  4
(x − 2) = 2
y =
(x − 2)(x − 4)
x − 4
lim
x  4
(x − 2)(x − 4)
x − 4
= 2
Observação
Dado um polinômio p de raízes x1, ...., xn, podemos fatorá-
lo em termos desses números.
anxn
+ an−1xn−1
… + a1x + a0
= an(x − x1)(x − x2). . . (x − xn)
Exemplo 1
lim
x  2
3x2
− 15x + 18
2x − 4
=
12 − 30 + 18
4 − 4
=
0
0
Como encontramos uma indeterminação 0/0, precisamos
fatorar os polinômios do numerador e denominador.
3x2
− 15x + 18 = 0
x2
− 5x + 6 = 0
x =
−b ± √b2 − 4ac
2a
=
5 ± √25 − 24
2
x1 = 2 x2 = 3
Isso significa que
ax2
+ bx + c = a(x − x1)(x − x2)
3x2
− 15x + 18 = 3(x − 2)(x − 3)
Assim,
lim
x  2
3x2
− 15x + 18
2x − 4
= lim
x  2
3(x − 2)(x − 3)
2(x − 2)
= lim
x  2
3(x − 3)
2
=
3(2 − 3)
2
= −
3
2
Exemplo 2
lim
x  1
2x − 2
x2 − 2x + 1
=
2 − 2
1 − 2 + 1
=
0
0
Como encontramos uma indeterminação 0/0, precisamos
fatorar os polinômios do numerador e denominador.
x2
− 2x + 1 = 0
x =
−b ± √b2 − 4ac
2a
=
2 ± √4 − 4
2
x1 = 1 x2 = 1
Logo,
lim
x  1
2(x − 1)
(x − 1)(x − 1)
= lim
x  1
2
x − 1
=
2
0
Para um problema assim, precisamos analisar pela direita e
pela esquerda.
lim
x  1−
2
x − 1
= −∞
lim
x  1+
2
x − 1
= +∞
Com isso, o limite em x = 1 não existe.
lim
x  a
𝑓(x)
𝑔(x)
=
0
0
Marquês de l'Hôpital
(1661 — 1704)

14. todaamatematica.com pág 13 engenhariae.com.br
Exemplo 3
lim
x  −2
x3
+ 8
x + 2
=
−8 + 8
−2 + 2
=
0
0
Como (−2)3
+ 8 = 0, x = −2 é raiz do polinômio do
numerador. Efetuando a divisão, encontramos que
x3
+ 8 = (x + 2)(x2
− 2x + 4)
x3
+ 8 |x + 2
−(x3
+ 2x2
) x2
− 2x + 4
−2x2
+ 8
−(−2x2
− 4x)
4x + 8
−(4x + 8)
0
Logo,
lim
x  −2
(x + 2)(x2
− 2x + 4)
x + 2
= lim
x  −2
(x2
− 2x + 4)
= (−2)2
− 2(−2) + 4 = 12
Exemplo 4
lim
x  9
x − 9
√x − 3
=
9 − 9
3 − 3
=
0
0
Para indeterminações assim, usaremos a fatoração
(a − b)(a + b) = a2
− b2
(√x − 3)(√x + 3) = x − 9
Assim,
= lim
x  9
x − 9
√x − 3
√x + 3
√x + 3
= lim
x  9
(x − 9)(√x + 3)
x − 9
= lim
x  9
(√x + 3) = √9 + 3 = 6
Exemplo 5
lim
x  0
√x + 4 − 2
x
=
2 − 2
0
=
0
0
Usando a fatoração (a − b)(a + b) = a2
− b2
,
= lim
x  0
√x + 4 − 2
x
√x + 4 + 2
√x + 4 + 2
= lim
x  0
(x + 4) − 4
x(√x + 4 + 2)
= lim
x  0
x
x(√x + 4 + 2)
= lim
x  0
1
√x + 4 + 2
=
1
√4 + 2
=
1
4
FUNÇÕES CONTÍNUAS
Exemplo 1
lim
x1−
𝑓(x) = 1
lim
x1+
𝑓(x) = 2
𝑓(1) = 2
lim
x1−
𝑓(x) = 1
lim
x1+
𝑓(x) = 1
𝑓(1) = 2
lim
x1−
𝑓(x) = 1
lim
x1+
𝑓(x) = 1
𝑓(1) = 1
De maneira intuitiva, notamos que para uma função ser
contínua num ponto é necessário que os limites laterais
existam, sejam iguais e coincidam com o valor da função.
Função contínua
Dizemos que 𝑓 é contínua em x = a se lim
xa
𝑓(x) = 𝑓(a)
O primeiro a preocupar-se
rigorosamente com a continuidade
foi Bolzano. Mas a definição atual é
de Cauchy.
Augustin Cauchy
(1789-1857)

15. todaamatematica.com pág 14 engenhariae.com.br
Observação
A sequência natural da disciplina de Cálculo é a de Análise
na reta. Ali, o rigor é a palavra chave e muitos conceitos são
revistos. A noção de função contínua, em particular, perde
totalmente sua intuição.
Num curso de Cálculo, dizemos que essa função é
descontínua em x = 1 . Num curso de Análise notamos que
a pergunta de fato não faz sentido.
Descontinuidades
Descontinuidade
removível
Descontinuidade salto
Descontinuidade infinita
Exemplo 2
A partir de 𝑓(x) = x + 2 conseguimos criar uma
descontinuidade removível em x = 1.
𝑓(x) = x + 2
𝑔(x) =
(x + 2)(x − 1)
x − 1
ℎ(x)
= {
(x + 2)(x − 1)
x − 1
, x  1
2, x = 1
Descontinuidade
removível
Exemplo 3
𝑓(x) =
x
|x|
Descontinuidade salto
𝑓(x) =
1
x
Descontinuidade infinita
Continuidade num intervalo
𝑓é contínua num intervalo (a, b) se for contínua em cada
ponto do intervalo. Para um intervalo [a, b], basta definir a
continuidade à direita de x = a
lim
xa+
𝑓(x) = 𝑓(a)
a continuidade à esquerda de x = b
lim
xb−
𝑓(x) = 𝑓(b)
Exemplo 4
𝑓(x) = √x − 1 é contínua
em [1, +)
lim
x1+
𝑓(x) = 𝑓(1) = 0
lim
x−2+
𝑓(x) = 𝑓(−2) = 0
lim
x2−
𝑓(x) = 𝑓(2) = 0
𝑓(x) = √4 − x2 é contínua
em [−2, 2]

16. todaamatematica.com pág 15 engenhariae.com.br
Teorema
Se 𝑓 e 𝑔 são contínuas em x = a, também são contínuas
nesse ponto
i) 𝑓 + 𝑔
ii) 𝑓 − 𝑔
iii) 𝑓𝑔
iv) 𝑓/𝑔, 𝑔(a)  0
Exemplo 5
São funções contínuas
y = c em todo o domínio.
y = x em todo o domínio.
Polinômios em todo o
domínio.
y = anxn
+ ⋯ + a1x + a0
Funções racionais são
contínua a exceção dos
pontos que apresentam
assíntotas verticais.
y =
anxn
+ ⋯ + a1x + a0
bmxm + ⋯ + b1x + b0
Exemplo 6
𝑓(x) = {
x − k, x < 2
x2
− 1, x  2
A função é contínua em x = 2 se
lim
x2−
𝑓(x) = 𝑓(2) = lim
x2+
𝑓(x)
lim
x2−
(x − k) = 22
− 1 = lim
x2+
(x2
− 1)
2 − k = 3
k = −1
Continuidade da função composta
Sejam 𝑓contínua em x = a e lim
xa
g(x) = L. Então
lim
xa
𝑓(g(x)) = 𝑓(lim
xa
g(x))
Exemplo 7
𝑓(x) = √x é contínua, com isso,
lim
x5
√2x − 3 = √lim
x5
(2x − 3) = √2.5 − 3 = √7
Exemplo 8
𝑓(x) = |x| é contínua, com isso,
lim
x1
|
x − 2
x2 + 1
|
= |lim
x1
x − 2
x2 + 1
|
= |
1 − 2
1 + 1
| =
1
2

17. todaamatematica.com pág 16 engenhariae.com.br
TEOREMA DO VALOR INTERMEDIÁRIO
Teorema do Valor Intermediário
Seja 𝑓 uma função contínua num intervalo [a, b]. Se k é um
número entre 𝑓(a) e 𝑓(b), então existe pelo menos um x =
c tal que 𝑓(c) = k.
Exemplo 1
A temperatura 𝑇 em C na qual a água ferve é dada
aproximadamente pela fórmula
𝑇(h) = 100,862 − 0,0415√h + 431,03
em que h é a altitude (em metros acima do nível do mar).
Pelo TVI, sabemos que a água ferve a 98C a uma altitude
entre 4 000 m e 4 500 m.
𝑇(4000) = 100,862 − 0,0415√4000 + 431,03 = 98,09
𝑇(4500) = 100,862 − 0,0415√4500 + 431,03 = 97,94
Observação
Bernard Bolzano
(1781-1848)
Em 1817, Bolzano provou o teorema numa versão
equivalente. O artigo era se chamava “Prova puramente
analítica do teorema que afirma que entre dois valores de
sinais opostos existe pelo menos uma raiz real da equação”.
Exemplo 2
A função 𝑓(x) = x5
− x − 2 tem pelo menos uma raiz no
intervalo[1, 2], pois
𝑓(1) = 1 − 1 − 2 < 0
𝑓(2) = 32 − 2 − 2 > 0
Pelo TVI, dado k = 0, existe x = c tal que 𝑓(c) = 0.
Exemplo 3
Um monge começou a caminhar em uma estrada de uma
montanha ao meio-dia e alcançou o topo à meia-noite. Ele
meditou e descansou até o meio-dia do dia seguinte, quando
começou a descer pela mesma estrada, alcançando a base à
meia-noite.
Mostre que há, no mínimo,
um ponto do caminho que
ele alcançou no mesmo
instante do dia, tanto na
subida quanto na descida.
Considere as funções subida 𝑠(𝑡) e descida 𝑑(𝑡), em que o
tempo é contado a partir do meio-dia do primeiro dia para a
função 𝑠 e a partir do meio-dia do segunda dia para a função
𝑑
𝑠(0) < 𝑑(0)
𝑠(12) > 𝑑(12)
Definindo a função 𝑓 = 𝑠 − 𝑑
𝑓(0) = 𝑠(0) − 𝑑(0) < 0
𝑓(12) = 𝑠(0) − 𝑑(0) > 0
Assim, pelo TVI, dado k = 0, existe horário t = c tal que
0 = 𝑓(c) = 𝑠(c) − 𝑑(c)
𝑑(c) = 𝑑(𝑐)
Observação
Sejam 𝑓 e 𝑔 funções contínuas em [a, b] tais que
𝑓(a) > 𝑔(a)
𝑓(b) < 𝑔(b).
Existe pelo menos um ponto x = c tal que 𝑓(c) = 𝑔(𝑐) em
(a, b).

18. todaamatematica.com pág 17 engenhariae.com.br
Exemplo 4
Se 𝑝 é um polinômio de grau ímpar, então 𝑝 tem pelo menos
uma raiz real.
Sem perda de generalidade,
lim
x +
𝑝 = +
lim
x −
𝑝 = −
Isso garante que existe um intervalo [a, b] tal que 𝑝(a) < 0
e 𝑝(b) > 0. Pelo TVI, dado k = 0, existe x = c tal
que 𝑝(c) = 0.
Observação
Considere a função 𝑓 que não é contínua.
𝑓(x)
= {sen (
1
x
) , x 0
1, x = 0
Se k é um número entre −1 e 1, então existe pelo menos
um x = c tal que 𝑓(c) = k. Com isso, função pode satisfazer
o Teorema do valor intermediário sem ser contínua.
Lebesgue chegou a
construir uma função que
satisfaz a propriedade do
valor intermediário, mas
não é contínua em um
ponto sequer.
Henri Lebesgue
(1875-1941)
CONTINUIDADE DAS FUNÇÕES
TRIGONOMÉTRICAS
As funções seno e cosseno são definidas no círculo
trigonométrico. De maneira intuitiva, quando o ponto
P(cos x , sen x) tende a A(cos a , sen a), temos que
lim
x→a
sen(x) = sen(a)
lim
x→a
cos(x) = cos(a)
Informalmente, os gráficos dessas funções indicam funções
contínuas.
y = sen(x)
y = cos(x)
A função tangente é contínua, exceto nos pontos que
anulam o denominador
lim
x→a
tan(x) = lim
x→a
sen(x)
cos(x)
=
sen(a)
cos(a)
= tan(a)
cos(a)  0
y = tan(x)
Exemplo 1
lim
x→1
sen (
2 − x
x
) = sen (lim
x→1
2 − x
x
) = sen(1)
lim
x→+∞
cos (
1
x
) = cos ( lim
x→+∞
1
x
) = cos(0) = 1
lim
x→+∞
sen (
πx
1 + 3x
) = sen ( lim
x→+∞
πx
1 + 3x
) = sen (
π
3
) =
√3
2

19. todaamatematica.com pág 18 engenhariae.com.br
Exemplo 2
A forma da Terra causa variações em sua gravidade 𝑔. Numa
cidade na latitude  ela vale aproximadamente
𝑔() = 9,78049(1 + 0,005264sen2
 + 0,000024sen4
)
A continuidade da função seno implica a continuidade de 𝑔.
Como
𝑔(35o) = 9,7974
𝑔(40o) = 9,8018
O Teorema do Valor Intermediário garante que existe
alguma latitude nesse intervalo tal que g = 9,8 m/s2
, o
valor adotado na maior parte dos livros
Observação
A exceção dos pontos que anulam os denominadores, de
maneira análoga, são contínuas as funções
sec(x) =
1
cos(x)
csc(x) =
1
sen(x)
cot(x) =
cos(x)
sen(x)
Continuidade da função inversa
Se 𝑓 é uma função contínua que possui inversa, então 𝑓−1
também é contínua.
De maneira intuitiva, o se o gráfico de 𝑓 não tem buracos,
então sua reflexão em torno da reta y = x também não tem
buracos.
São contínuas as funções arco seno e arco cosseno.
seno arco seno
cosseno arco cosseno
Exemplo 3
lim
x→+∞
arc sen (
2x
1 + 4x
)
= arcsen ( lim
x→+∞
2x
1 + 4x
)
= arcsen (
1
2
) =
π
6
Observação
Também são contínuas as funções arco tangente e arco
cotangente.
tangente arco tangente

20. todaamatematica.com pág 19 engenhariae.com.br
cotangente arco cotangente
As funções arco secante e arco cossecante não estão
definidas para todo x.
secante arco secante
cossecante arco cossecante
TEOREMA DO CONFRONTO
Teorema do confronto (ou da sanduíche)
Sejam 𝑓(x)  𝑔(x)  ℎ(x) e
lim
x→a
𝑓(x) = lim
x→a
𝑔(x) = lim
x→a
ℎ(x)
com
lim
x→a
𝑓(x) = L = lim
x→a
ℎ(x)
Então
lim
x→a
𝑔(x) = L
Exemplo 1
lim
x→0
xsen (
1
x
) = ?
y = sen (
1
x
)
|sen (
1
x
)|  1
|xsen (
1
x
)|  |x|
−|x|  xsen (
1
x
)  |x|
Como lim
x→0
|x| = 0, então
Logo,
lim
x→0
xsen (
1
x
) = 0

21. todaamatematica.com pág 20 engenhariae.com.br
Exemplo 2
lim
x→0
sen(x)
x
=?
A =
sen(x)
2
x
A
=
2π
π. 12
A =
x
2
A =
tan(x)
2
Com isso,
tan(x)
2

x
2

sen(x)
2
tan(x)  x  sen(x)
sen(x)
cos(x)
 x  sen(x)
Para x > 0 e pequeno,
1
cos(x)

x
sen(x)
 1
cos(x) 
sen(x)
x
 1
lim
x→0+
cos(x) = lim
x→0+
sen(x)
x
= lim
x→0+
1
1 = lim
x→0+
sen(x)
x
= 1
Também vale que
lim
x→0−
sen(x)
x
= 1
Pois a substituição x por – x não altera
cos(x) 
sen(x)
x
 1
Logo,
lim
x→0
sen(x)
x
= 1
y =
sen(x)
x
Exemplo 3
Para qualquer 𝑓 tal que cos(x)  𝑓(x)  1 − x2
, vale que
lim
x→0
cos(x) = 1 = lim
x→0
1 − x2
lim
x→0
𝑓(x) = 1
Exemplo 4
lim
x→+
sen(x)
x
= ?
Como
−
1
x

sen(x)
x

1
x
e
lim
x→+
1
x
= 0
então
lim
x→+
sen(x)
x
= 0
Observação
O Teorema do confronto também se chama Teorema do
Sanduíche. Existe outro resultado com o mesmo nome.
Considere um sanduíche forma por duas fatias de pão (com
formato qualquer) recheados com uma fatia de presunto
(colocado de qualquer forma). Em 1938, Banach provou que
existe uma maneira de cortar o alimento em duas partes que
ficam com a mesma quantidade de ingredientes.
Stefan Banach
(1892 1945)

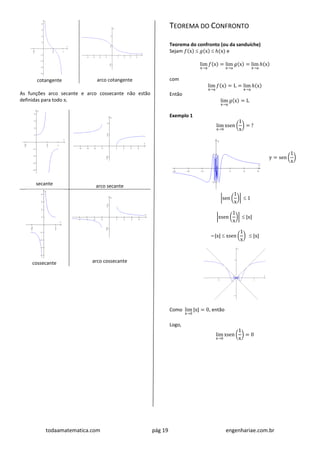
22. todaamatematica.com pág 21 engenhariae.com.br
LIMITES TRIGONOMÉTRICOS
Observação
lim
x→0
sen(x)
x
= 1
Exemplo 1
Com a mudança de variáveis y = 3x
lim
x→0
sen(3x)
x
= lim
y→0
sen(y)
y
3
= 3 lim
y→0
sen y
y
= 31 = 3
Outra solução é
lim
x→0
sen(3x)
x
= lim
x→0
3sen(3x)
3x
= 3 lim
x→0
sen(3x)
3x
= 31 = 3
Observação
Na prática,
lim
x→0
sen 

= 1
Exemplo 2
lim
x→0
sen(4x)
sen (5x)
= lim
x→0
sen(4x)
x
sen(5x)
x
= lim
x→0
4sen(4x)
4x
5sen(5x)
5x
=
4
5
lim
x→0
sen(4x)
4x
sen(5x)
5x
=
4
5

1
1
=
4
5
Exemplo 3
lim
x→0+
sen(x)
x2
= lim
x→0+
1
x
.
sen(x)
x
= +
Exemplo 4
lim
x→0
[sen(x)]2
x
= lim
x→0
sen(x)
sen(x)
x
= 01 = 0
Exemplo 5
lim
x→0
tan(x)
x
= lim
x→0
sen(x)
cos(x)
1
x
= lim
x→0
sen(x)
x
1
cos(x)
= 11 = 1
Exemplo 6
lim
x→0
1 − cos(x)
x
= lim
x→0
1 − cos(x)
x
1 + cos(x)
1 + cos(x)
Como (a − b)(a + b) = a2
− b2
= lim
x→0
1 − [cos(x)]2
x
1
1 + cos(x)
Como [cos(x)]2
+ [sen (x)]2
= 1
= lim
x→0
[sen(x)]2
x
1
1 + cos(x)
= lim
x→0
sen(x)
x
sen(x)
1 + cos(x)
= 1
0
1 + 1
= 0
Exemplo 7
lim
x→0
1 − cos(x)
x2
= lim
x→0
1 − cos(x)
x2
1 + cos(x)
1 + cos(x)
= lim
x→0
1 − [cos(x)]2
x2
1
1 + cos(x)
= lim
x→0
[sen(x)]2
x2
1
1 + cos(x)
= lim
x→0
[
sen(x)
x
]
2
1
1 + cos(x)
= 12
1
1 + 1
=
1
2