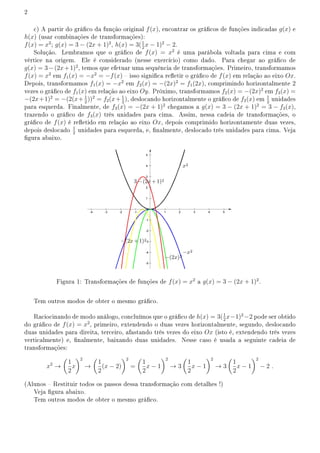
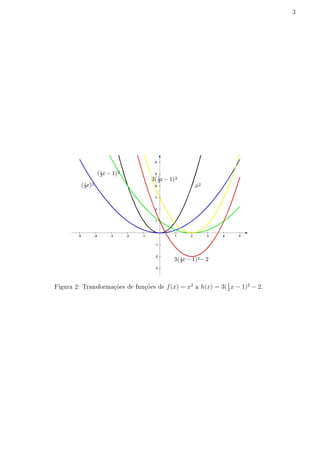
1) O documento discute transformações de funções e seus gráficos, incluindo translações horizontais e verticais, extensões e compressões horizontais e verticais, e combinações de transformações. 2) Exemplos detalhados são fornecidos para transformar gráficos de funções originais em gráficos de novas funções usando essas técnicas. 3) Figuras ilustram as etapas das transformações de funções para chegar aos gráficos solicitados.

1. 1
Transformações de funções e seus grácos.
Lista 10a - com respostas no livro/folha de exercícios e atendimento.
Atenção. As respostas devem ser completas, contendo todo o desenvolvimento lógico devido.
Somente conclusões nais não serão aceitas.
1. Demana p.120:
N 1, 3, 5
2. Exercícios adicionais:
a) A partir do gráco da função original f(x), encontrar os grácos de funções indicadas g(x) e
h(x) (usar translações horizontais e verticais):
f(x) = x2
; g(x) = (x − 1)2
+ 2, h(x) = (x + 2)2
− 1.
Solução.
Lembramos que o gráco de f(x) = x2
é uma parábola voltada para cima e com vértice na origem.
Esse gráco é considerado (nesse exercício) como dado. Lembramos que a transformação de f(x)
para f(x + c), qualquer que for f(x), resulta na translação horizontal do gráco de f(x) de c
unidades para esquerda (sendo para c negativo a translação se faz |c| unidades para direita). Assim,
partindo do gráco de f(x) = x2
chegamos, primeiro, ao gráco de ˜
f(x) = (x − 1)2
= f(x − 1)
deslocando o primeiro 1 unidade para direita. Agora, considerando o último como dado, faremos
mais uma transformação para obter g(x) = (x − 1)2
+ 2. Comparando ˜
f(x) e g(x), notamos que
g(x) = ˜
f(x) + 2, o que signica (geometricamente) a translação vertical do gráco de ˜
f(x) de 2
unidades para cima. (Lembramos que a transformação de f(x) para f(x) + c, qualquer que for
f(x), resulta na translação vertical do gráco de f(x) de c unidades para cima, o que no caso de c
negativo é interpretado como |c| unidades para baixo.) Assim, o gráco de g(x) = (x − 1)2
+ 2 é
obtido do gráco de f(x) = x2
deslocando o último 1 unidade para direita e 2 unidades para cima.
Raciocinando de modo análogo, podemos concluír que o gráco de h(x) = (x + 2)2
− 1 pode
ser obtido do gráco de f(x) = x2
deslocando o último 2 unidades para esquerda e 1 unidade para
baixo. (Alunos Restituir todos os passos dessa transformação !)
b) A partir do gráco da função original f(x), encontrar os grácos de funções indicadas g(x) e
h(x) (usar extensões e compressões horizontais e verticais):
f(x) = |2x|; g(x) = |1
3
x|, h(x) = −|2x|.
Solução.
Lembramos que o gráco de f(x) = |2x| consiste de duas partes retilíneas −2x, para x ≤ 0 e 2x
para x ≥ 0 as quais se encontram na origem (que é vértice desse gráco). Ele é considerado (nesse
exercício) como dado. Para chegar ao gráco de g(x) = |1
3
x|, podemos alongar (extender) o gráco
original 6 vezes na horizontal, uma vez que g(x) = |1
6
2x| = f(1
6
x). (Lembramos que a transformação
de f(x) para f(cx), c 0, qualquer que for f(x), resulta na extenção horizontal do gráco 1
c
vezes
caso c 1 e compressão c vezes caso c 1; se c 0, então aplicamos as mesmas transformações
com |c|, acrescidas da reexão do gráco em torno do eixo Oy.)
A maneira alternativa é levar tudo a extensão/compressão vertical. Para isso, podemos reescrever
g(x) na forma equivalente g(x) = 1
6
|2x| = 1
6
f(x). Então, para obter o gráco de g(x), podemos
comprimir o gráco original 6 vezes na vertical. (Lembramos que a transformação de f(x) para
cf(x), c 0, qualquer que for f(x), resulta na extenção vertical do gráco c vezes caso c 1
e compressão 1
c
vezes caso c 1; se c 0, então aplicamos as mesmas transformações com |c|,
acrescidas da reexão do gráco em torno do eixo Ox.)
Para obter o gráco de h(x) = −|2x| = −f(x), lembramos que multiplicação da função por −1
resulta em reexão do seu gráco em torno do eixo Ox.

2. 2
c) A partir do gráco da função original f(x), encontrar os grácos de funções indicadas g(x) e
h(x) (usar combinações de transformações):
f(x) = x2
; g(x) = 3 − (2x + 1)2
, h(x) = 3(1
2
x − 1)2
− 2.
Solução. Lembramos que o gráco de f(x) = x2
é uma parábola voltada para cima e com
vértice na origem. Ele é considerado (nesse exercício) como dado. Para chegar ao gráco de
g(x) = 3−(2x+1)2
, temos que efetuar uma sequência de transformações. Primeiro, transformamos
f(x) = x2
em f1(x) = −x2
= −f(x) isso signica reetir o gráco de f(x) em relação ao eixo Ox.
Depois, transformamos f1(x) = −x2
em f2(x) = −(2x)2
= f1(2x), comprimindo horizontalmente 2
vezes o gráco de f1(x) em relação ao eixo Oy. Próximo, transformamos f2(x) = −(2x)2
em f3(x) =
−(2x+1)2
= −(2(x+ 1
2
))2
= f2(x+ 1
2
), deslocando horizontalmente o gráco de f2(x) em 1
2
unidades
para esquerda. Finalmente, de f3(x) = −(2x + 1)2
chegamos a g(x) = 3 − (2x + 1)2
= 3 − f3(x),
trazendo o gráco de f3(x) três unidades para cima. Assim, nessa cadeia de transformações, o
gráco de f(x) é reetido em relação ao eixo Ox, depois comprimido horizontamente duas vezes,
depois deslocado 1
2
unidades para esquerda, e, nalmente, deslocado três unidades para cima. Veja
gura abaixo.
Figura 1: Transformações de funções de f(x) = x2
a g(x) = 3 − (2x + 1)2
.
Tem outros modos de obter o mesmo gráco.
Raciocinando de modo análogo, concluímos que o gráco de h(x) = 3(1
2
x−1)2
−2 pode ser obtido
do gráco de f(x) = x2
, primeiro, extendendo o duas vezes horizontalmente, segundo, deslocando
duas unidades para direita, terceiro, afastando três vezes do eixo Ox (isto é, extendendo três vezes
verticalmente) e, nalmente, baixando duas unidades. Nesse caso é usada a seguinte cadeia de
transformações:
x2
→
(
1
2
x
)2
→
(
1
2
(x − 2)
)2
=
(
1
2
x − 1
)2
→ 3
(
1
2
x − 1
)2
→ 3
(
1
2
x − 1
)2
− 2 .
(Alunos Restituir todos os passos dessa transformação com detalhes !)
Veja gura abaixo.
Tem outros modos de obter o mesmo gráco.

3. 3
Figura 2: Transformações de funções de f(x) = x2
a h(x) = 3(1
2
x − 1)2
− 2.