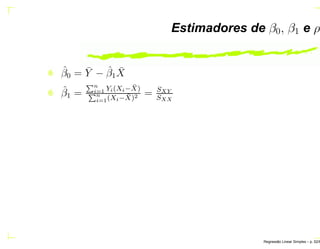
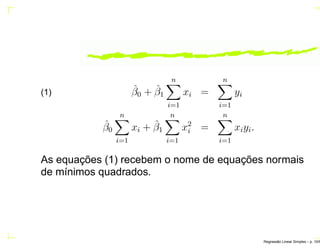
O documento discute regressão linear simples, apresentando seu objetivo de estudar a relação linear entre duas variáveis quantitativas através de coeficientes de regressão. Exemplos incluem a relação entre altura dos pais e filhos. O método dos mínimos quadrados ordinários é usado para estimar os parâmetros da função de regressão a partir de dados amostrais.

1. Regressão Linear Simples
V´ıctor Hugo Lachos D´avila
hlachos@ime.unicamp.br
Departamento Estat´ıstica-IMECC
Universidade Estadual de Campinas
Campinas, S˜ao Paulo, Brasil
Regress˜ao Linear Simples – p. 1/6

2. Objetivos
Estudar a relação linear entre duas variáveis quantitativas.
Veja alguns exemplos:
Altura dos pais e altura dos filhos(Fig 1);
Regress˜ao Linear Simples – p. 2/6

3. Objetivos
Estudar a relação linear entre duas variáveis quantitativas.
Veja alguns exemplos:
Altura dos pais e altura dos filhos(Fig 1);
Renda semanal e despensas de consumo;
Regress˜ao Linear Simples – p. 2/6

4. Objetivos
Estudar a relação linear entre duas variáveis quantitativas.
Veja alguns exemplos:
Altura dos pais e altura dos filhos(Fig 1);
Renda semanal e despensas de consumo;
Variação dos salarios e taxa de desemprego (Fig 2);
Regress˜ao Linear Simples – p. 2/6

5. Objetivos
Estudar a relação linear entre duas variáveis quantitativas.
Veja alguns exemplos:
Altura dos pais e altura dos filhos(Fig 1);
Renda semanal e despensas de consumo;
Variação dos salarios e taxa de desemprego (Fig 2);
Demanda dos productos de uma firma e publicidade;
Regress˜ao Linear Simples – p. 2/6

6. Objetivos
Estudar a relação linear entre duas variáveis quantitativas.
Veja alguns exemplos:
Altura dos pais e altura dos filhos(Fig 1);
Renda semanal e despensas de consumo;
Variação dos salarios e taxa de desemprego (Fig 2);
Demanda dos productos de uma firma e publicidade;
Sob dois pontos de vista:
Explicitando a forma dessa relação: regress˜ao.
Quantificando a força dessa relação: correlac¸ ˜ao.
Regress˜ao Linear Simples – p. 2/6

7. Observações
1) Regressão vs Causação
Uma relação estatística por sí propria não implica uma
causação
Para atribuir causação, devemos invocar a alguma
teoría (p.e. econômica)
2) Regressão (AR) vs Correlação (AC)
na AC há tratamento simetrico das variáveis
na AR a variável explanatoria é fixa
na AC presupõe-se que as duas variaveís são
aleatórias
Regress˜ao Linear Simples – p. 3/6

8. Dados Hipotéticos
Os dados se referem à renda semanal (X) e as despensas
de consumo (Y) (em US$), de uma população total de 60
familias. As 60 familias foram divididas em 10 grupos de
renda (Fig 3 e 4).
Y 80 100 120 140 160 180 200 220 240 260
55 65 79 80 102 110 120 135 137 150
60 70 84 93 107 115 136 137 145 152
65 74 90 95 110 120 140 140 155 175
X 70 80 94 103 116 130 144 152 165 178
75 85 98 108 118 135 145 157 175 180
- 88 - 113 125 140 - 160 189 185
- - - 115 - - - 162 - 191
Total 325 462 445 707 678 750 685 1043 966 1211
E(Y|X) 65 77 89 101 113 125 137 149 161 173
Regress˜ao Linear Simples – p. 4/6

9. Função de Regressão Populacional
É razoável supor que a média da variável aleatória Y , está
relacionada com X pela seguinte relação
E(Y |X = x) = µY |x = β0 + β1x
onde βo e β1, são respectivamente, o intercepto e a
inclinação da reta e recebem o nome de coeficientes de
regressão.
Regress˜ao Linear Simples – p. 5/6

10. Função de Regressão Populacional
É razoável supor que a média da variável aleatória Y , está
relacionada com X pela seguinte relação
E(Y |X = x) = µY |x = β0 + β1x
onde βo e β1, são respectivamente, o intercepto e a
inclinação da reta e recebem o nome de coeficientes de
regressão.
Cada valor individual Yi será determinado pelo valor médio
da função linear (µY |x) mais um termo que representa um
erro aleatório,
Regress˜ao Linear Simples – p. 5/6

11. Função de Regressão Populacional
É razoável supor que a média da variável aleatória Y , está
relacionada com X pela seguinte relação
E(Y |X = x) = µY |x = β0 + β1x
onde βo e β1, são respectivamente, o intercepto e a
inclinação da reta e recebem o nome de coeficientes de
regressão.
Cada valor individual Yi será determinado pelo valor médio
da função linear (µY |x) mais um termo que representa um
erro aleatório,
Yi = µY |x + εi = β0 + β1xi + εi,
onde εi é o erro estocástico que satisfaz E(εi|xi) = 0Regress˜ao Linear Simples – p. 5/6

12. Em geral, a variável resposta pode estar relacionada com
k variáveis explicativas X1, . . . Xk obedecendo à equação :
Y = β0 + β1X1 + . . . + βkXk + ε,
A equação é denominada modelo de regressão linear
múltipla.
Regress˜ao Linear Simples – p. 6/6

13. Em geral, a variável resposta pode estar relacionada com
k variáveis explicativas X1, . . . Xk obedecendo à equação :
Y = β0 + β1X1 + . . . + βkXk + ε,
A equação é denominada modelo de regressão linear
múltipla.
O adjetivo "linear"é usado para indicar que o modelo é
linear nos parâmetros β1, . . . , βk e não porque Y é função
linear dos X’s. Por exemplo, uma expressão da forma
Y = βo + β1 log X1 + β2X3
2 + ε é um modelo de regressão
linear múltipla, mas o mesmo não acontece com a
equação Y = β0 + β1Xβ2
1 + β3X2
2 + ε.
Regress˜ao Linear Simples – p. 6/6

14. Significado do erro estocástico
Caráter vago da teoria
Falta de dados disponíveis
Variávies essenciais vs variáveis periféricas
Caráter aleatório da natureza
Principio da parcimônia
Forma funcional equivocada
Regress˜ao Linear Simples – p. 7/6

15. Função de Regressão Amostral(FRA)
A tarefa agora é estimar a FRP com base em informações
amostrais
Yi = Yi + εi = β0 + β1Xi + εi, i = 1, . . . , n,
onde β0 e β1 são estimadores de β0 e β1, respectivamente
e εi = Yi − Yi a componente residual (Fig 5). Precisamos
formular uma regra ou método que torne tal aproximação o
mais próximo possível!
Exercicio: Resolva o problema 2.16 do livro texto.
Regress˜ao Linear Simples – p. 8/6

16. Estimação: Método de MQO
Suponha que tem-se n pares de observações amostrais
(x1, y1), . . . , (xn, yn). A soma de quadrados dos desvios
das observações em relação à FRA é:
Q =
n
ε2
i =
n
(yi − β0 − β1xi)2
.
O método de mínimos quadrados ordinarios (MQO)
escolhe β1 e β2 (únicos) de forma que, para qualquer
amostra, Q é o menor possível. Após uma simple algebra
tem-se
Regress˜ao Linear Simples – p. 9/6

17. ˆβ0 + ˆβ1
n
i=1
xi =
n
i=1
yi(1)
ˆβ0
n
i=1
xi + ˆβ1
n
i=1
x2
i =
n
i=1
xiyi.
As equações (1) recebem o nome de equações normais
de mínimos quadrados.
Regress˜ao Linear Simples – p. 10/6

18. A solução dessas equações fornece os EMQ, ˆβ0 e ˆβ1,
dados por:
ˆβ0 = ¯y − ˆβ1 ¯x.
ˆβ1 =
n
i=1
xiyi −
nÈ
i=1
xi
nÈ
i=1
yi
n
n
i=1
x2
i −
nÈ
i=1
xi
2
n
.
onde ¯x =
nÈ
i=1
xi
n
e ¯y =
nÈ
i=1
yi
n
.
Regress˜ao Linear Simples – p. 11/6

19. Notações especiais
Sxx =
n
i=1
(xi − ¯x)2
=
n
i=1
x2
i −
nÈ
i=1
xi
2
n
=
n
i=1
x2
i − n¯x2
,
Sxy =
n
i=1
(xi − ¯x)(yi − ¯y) =
n
i=1
(xi − ¯x)yi =
n
i=1
xiyi −
nÈ
i=1
xi
nÈ
i=1
yi
n
=
n
i=1
xiyi − n¯x¯y,
Syy =
n
i=1
(yi − ¯y)2
=
n
i=1
(yi − ¯y)yi =
n
i=1
y2
i −
nÈ
i=1
yi
2
n
=
n
i=1
y2
i − n¯y2
.
Os EMQ de β0 e β1 em termos da notação acima são:
ˆβ0 = ¯y − ˆβ1 ¯x, ˆβ1 =
Sxy
Sxx
, yi − ¯y = β1(xi − ¯x).
Regress˜ao Linear Simples – p. 12/6

20. Observaçoes sobre os EMQ
Os EMQ dependem só de quantidades observáveis
São estimadores pontuais
A linha de regressão amostral é facilmente obtida
Yi = β0 + β1Xi
O valor médio do resíduo ǫi é zero
Os residuos ǫi são não correlacionados com Xi e Yi.
Regress˜ao Linear Simples – p. 13/6

21. Exemplo 1
O gerente de uma cadeia de supermercados deseja
desenvolver um modelo com a finalidade de estimar as
vendas médias semanais (em milhares de dólares)
Y - Vendas semanais; e
X - Número de clientes.
Estas variáveis foram observadas em 20 supermercados
escolhidos aleatóriamente.
X 907 926 506 741 789 889 874 510 529 420
Y 11,20 11,05 6,84 9,21 9,42 10,08 9,45 6,73 7,24 6,12
X 679 872 924 607 452 729 794 844 1010 621
Y 7,63 9,43 9,46 7,64 6,92 8,95 9,33 10,23 11,77 7,41
Regress˜ao Linear Simples – p. 14/6

22. Aplicação
Considerando os dados do exemplo 1
n = 20
n
i=1
xi = 907 + 926 + . . . + 621 = 14.623; ¯x = 731, 15
n
i=1
yi = 11, 20 + 11, 05 + . . . + 7, 41 = 176, 11; ¯y = 8, 8055
n
i=1
x2
i = (907)2
+ (926)2
+ . . . + (621)2
= 11.306.209
n
i=1
y2
i = (11, 20)2
+ (11, 05)2
+ . . . + (7, 41)2
= 1.602, 0971
n
i=1
xiyi = (907)(11, 20) + (11, 05)(926) . . . + (7, 41)(621) = 134.127, 90
Regress˜ao Linear Simples – p. 15/6

23. Sxx =
n
i=1
x2
i − n(¯x)2
= 11.306.209 − 20(731, 15)2
= 614.603
Sxy =
n
i=1
xiyi − n(¯x)(¯y) = 134.127, 90 − 20(8, 8055)(731, 15) = 5.365, 08
Syy =
n
i=1
y2
i − n(¯y)2
= 1.609, 0971 − 20(8, 8055) = 51, 3605.
As estimativas dos parâmetros do MRLS são:
ˆβ1 =
Sxy
Sxx
=
5.365, 08
614.603
= 0, 00873; ˆβ0 = ¯y−ˆβ1 ¯x = 8, 8055−(0, 00873)(731, 15) = 2, 423
Portanto, a linha de regressão ajustada ou estimada para esses dados são:
ˆy = 2, 423 + 0, 00873x.
Regress˜ao Linear Simples – p. 16/6

24. 400 500 600 700 800 900 1000
67891011
Numero de clientes
Vendassemanais
Regress˜ao Linear Simples – p. 17/6

25. Suponha que tem-se interesse em prever as vendas
semanais para um supermercado com 600 clientes.
No modelo de regressão ajustado basta substituir
X = 600, ísto é,
ˆy = 2, 423 + (0, 00873)(600) = 7, 661.
Regress˜ao Linear Simples – p. 18/6

26. Suponha que tem-se interesse em prever as vendas
semanais para um supermercado com 600 clientes.
No modelo de regressão ajustado basta substituir
X = 600, ísto é,
ˆy = 2, 423 + (0, 00873)(600) = 7, 661.
A venda semanal de 7,661 mil dólares pode ser
interpretada com uma estimação da venda média semanal
verdadeira dos supermercados com X = 600 clientes,
Regress˜ao Linear Simples – p. 18/6

27. Suponha que tem-se interesse em prever as vendas
semanais para um supermercado com 600 clientes.
No modelo de regressão ajustado basta substituir
X = 600, ísto é,
ˆy = 2, 423 + (0, 00873)(600) = 7, 661.
A venda semanal de 7,661 mil dólares pode ser
interpretada com uma estimação da venda média semanal
verdadeira dos supermercados com X = 600 clientes, ou
como uma estimação de uma futura venda de um
supermercado quando o número de clientes for X = 600.
Regress˜ao Linear Simples – p. 18/6

28. Suposições do método de MQO
(i) E(ε|X) = 0, V ar(ε|X) = σ2
(desconhecido).
(ii) Os erros são não correlacionados
(iii) A variável explicativa X é controlada pelo
experimentador.
(iv) o modelo de regressão esta especificado da forma
correta
(v) n> número de variáveis explanatorias
(iv) não ha multicolinearidade perfeita
Regress˜ao Linear Simples – p. 19/6

29. Propriedades dos EMQ
Se as suposições do método de MQO são válidas, então
E(ˆβ1) = β1, V ar(ˆβ1) = σ2
Sxx
= σ2
β1
.
E(ˆβ0) = β0, V ar(ˆβ0) = σ2 1
n
+ ¯x2
Sxx
= σ2
β0
.
Cov(ˆβ0, ˆβ1) = −σ2 ¯x
Sxx
Exercicio 2.
Regress˜ao Linear Simples – p. 20/6

30. Estimação de σ2
Os resíduos,
ei = yi − ˆyi
são empregados na estimação de σ2
. A soma de
quadrados residuais ou soma de quadrados dos erros,
denotado por SQR é:
SQR =
n
i=1
e2
i =
n
i=1
(yi − ˆyi)2
Pode-se demonstrar que o valor esperado da soma de
quadrados dos residuais SQR, é dado por:(Exercício 3)
E(SQR) = (n − 2)σ2
Regress˜ao Linear Simples – p. 21/6

31. Portanto, um estimador não viciado de σ2
, é
ˆσ2 =
SQR
n − 2
= QMR (Quadrado m´edio residual),
Uma fórmula mais conveniente para o cálculo da SQR é
dada por:
SQR = Syy − ˆβ1Sxy.
A estimativa de σ2
para o exemplo 1.
ˆσ2 =
SQR
n − 2
=
Syy − ˆβ1Sxy
n − 2
=
51, 3605 − (0, 00873)(5.365, 08)
20 − 2
= 0, 2513.
Regress˜ao Linear Simples – p. 22/6

32. Previsão
Seja xp o valor para o qual deseja-se prever (ou projetar) o
valor médio E(Y |xp) e o valor individual de Y .
- Previsão média
Yi é um estimador não viciado de E[Y |xp], dado que
E(Yi) = E(ˆβ0 + ˆβ1xp) = β0 + β1xp = E(Y |xp)
V ar(Yi) = σ2
[1
n
+ (xi−¯x)2
sxx
]
- Previsão individual (Exercicio 4.)
V ar(Ypart) = σ2
[1 + 1
n
+ (xi−¯x)2
sxx
]
Na pratica sustituimos σ2
(desconhecido), pelo estimador
consistente σ2 Regress˜ao Linear Simples – p. 23/6

33. Coeficiente de Determinação (r2
)
O r2
é uma medida de qualidade do ajustamento. No caso
de regressão linear simples o coeficiente de determinação
é o quadrado do coeficiente de correlação.(Fig 6)
(Yi − ¯Y ) = (Yi − ˆYi − ¯Y + ˆYi)
n
i=1
(Yi − ¯Y )2
=
n
i=1
( ˆYi − ¯Y )2
+
n
i=1
(Yi − ˆYi)2
SQT = SQM + SQR
1 =
SQM
SQT
+
SQR
SQT
⇒ r2
=
SQM
SQT
=
s2
xy
sxxsyy
Regress˜ao Linear Simples – p. 24/6

34. Teorema de Gauss-Markov
Se as suposições MQO são satisfeitas, os EMQ da classe
de estimadores lineares não viesados têm variância
mínima, isto é, são os melhores estimadores lineares não
viesados. (Prova)
Para que normalidade?
A estimação é a metade do caminho, a outra metade é
teste se hipóteses, para isto, suposições adicionais são
necessárias.
uma alternativa é considerar tamanhos de amostra o
suficientemente grandes (estimação de máxima
verossimilhança)
a outra é supor que ǫi ∼ N(0, σ2
) (O modelo de
regressão normal simple clássico)
Regress˜ao Linear Simples – p. 25/6

35. Propiedades dos EMQ sob Normalidade
A justificão teórica da premissa de normalidade é o TLC
β1 =
n
i=1
kiYi =
n
i=1
ki(β1 + β2xi + ǫi) ∼ N(.)
β0 ∼ N(β0, σ2
β0
), β1 ∼ N(β1, σ2
β1
),
(n − 1)σ2
/σ2
∼ χ2
(n − 2)
A distribuição de β0 e β1 é independente de σ2
(Exercicio 5.)
β0 e β1 têm variância mínima dentro de toda classe dos
estimadores não viesados, sejam ou não lineares (Rao)
Yi|Xi ∼ N(β0 + β1Xi, σ2
) Regress˜ao Linear Simples – p. 26/6

36. Teste de hipóteses sobre β1
Suponha que se deseje testar a hipótese de que a
inclinação é igual a uma constante representada por β1,0.
As hipóteses apropriadas são:
H0 : β1 = β1,0, vs H1 : β1 = β1,0
A estatística
T =
ˆβ1 − β1,0
ˆσ2/Sxx
,
tem distribuição t-Student com n − 2 graus de liberdade
sob H0 : β1 = β1,0. Rejeita-se H0 se
|Tobs| > tα/2, n−2.
Regress˜ao Linear Simples – p. 27/6

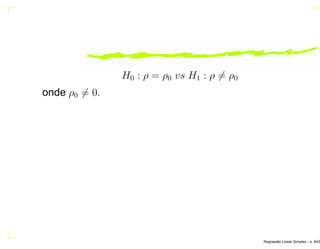
37. Teste de hipóteses sobre β0
H0 : β0 = β0,0, vs H1 : β0 = β0,0
A estatística
T =
ˆβ0 − β0,0
ˆσ2[1
n
+ ¯x2
Sxx
]
que tem distribuição t-Student com n − 2 graus de
liberdade. Rejeitamos a hipóteses nula se |Tobs| > tα/2, n−2.
Regress˜ao Linear Simples – p. 28/6

38. Teste de significância do MRLS
H0 : β1 = 0, vs H1 : β1 = 0,
Deixar de rejeitar H0 : β1 = 0 é equivalente a concluir que
não há nenhuma relação linear entre X e Y.
Regress˜ao Linear Simples – p. 29/6

39. Se H0 : β1 = 0 é rejeitado, implica que X tem importância
para explicar a variabilidade de Y
Regress˜ao Linear Simples – p. 30/6

40. Exemplo
Teste de significância para o MRLS para os dados do
exemplo 1, com α = 0, 05.
As hipóteses são H0 : β1 = 0, vs H1 : β1 = 0
Do exemplo tem-se:
ˆβ1 = 0, 00873, n = 20 Sxx = 614, 603, ˆσ2
= 0, 2512,
De modo que a estatística de teste, é:
Tobs =
ˆβ1
ˆσ2/Sxx
=
0, 00873
0, 2513/614.603
= 13, 65.
Como Tobs = 13, 65 > t0,03,18 = 2, 101, rejeita-se a hipótese
H0 : β1 = 0.
Regress˜ao Linear Simples – p. 31/6

41. Análise de variância
Se a hipótese nula H0 : β1 = 0 é verdadeira, a estatística
F =
SQM/1
SQR/(n − 2)
=
QMreg
QMR
∼ F(1, n − 2),
Portanto, rejeita-se H0 se F0bs > Fα, 1, n−2.
As quantidades
QMreg = SQM
1
, (quadrado médio devido à regressão) e
QMR = SQR
(n−2)
( quadrado médio residual)
Regress˜ao Linear Simples – p. 32/6

42. Tabela de ANOVA
Fonte de Soma de Graus de Quadrado
variação Quadrados Liberdade Médio F
Regressão SQM 1 QMreg QMreg
QMR
Residual SQR n − 2 QMR
Total SQT n − 1
Regress˜ao Linear Simples – p. 33/6

43. Tabela de ANOVA
Fonte de Soma de Graus de Quadrado
variação Quadrados Liberdade Médio F
Regressão SQM 1 QMreg QMreg
QMR
Residual SQR n − 2 QMR
Total SQT n − 1
Exemplo: o procedimento de análise de variância para
testar se de fato existe relação linear entre o número de
clientes (X) e as vendas semanais (Y), no modelo
proposto para os dados do exemplo 1. Relembre que
Syy = 51, 3605, ˆβ1 = 0, 00873, Sxy = 5.365, 08 e n = 20.
Regress˜ao Linear Simples – p. 33/6

44. A soma de quadrados da regressão é
SQM = ˆβ1Sxy = (0, 00873)(5.365, 08) = 46, 8371
enquanto a soma de quadrados dos residuais é:
SQR = SQT − ˆβ1Sxy = 51, 3605 − 46, 8371 = 4, 5234
Regress˜ao Linear Simples – p. 34/6

45. A soma de quadrados da regressão é
SQM = ˆβ1Sxy = (0, 00873)(5.365, 08) = 46, 8371
enquanto a soma de quadrados dos residuais é:
SQR = SQT − ˆβ1Sxy = 51, 3605 − 46, 8371 = 4, 5234
A ANOVA para testar H0 : β1 = 0. Nesse caso, a
estatística de teste é
F0bs = QMreg/QMR = 46, 837148/0, 2512 = 186, 4536.
Regress˜ao Linear Simples – p. 34/6

46. A soma de quadrados da regressão é
SQM = ˆβ1Sxy = (0, 00873)(5.365, 08) = 46, 8371
enquanto a soma de quadrados dos residuais é:
SQR = SQT − ˆβ1Sxy = 51, 3605 − 46, 8371 = 4, 5234
A ANOVA para testar H0 : β1 = 0. Nesse caso, a
estatística de teste é
F0bs = QMreg/QMR = 46, 837148/0, 2512 = 186, 4536.
Como Fobs = 186, 4536 > F0,05,1,18 = 4, 41 rejeita-se H0, ao
nível de significância de 5%.
Regress˜ao Linear Simples – p. 34/6

47. Tabela de ANOVA para Ex. 1
Fonte de Soma de Graus de Quadrado
variação Quadrados Liberdade Médio F
Regressão 46, 8371 1 46, 8371 186,45
Residual 4, 5234 18 0, 2513
Total 51, 3605 19
Regress˜ao Linear Simples – p. 35/6

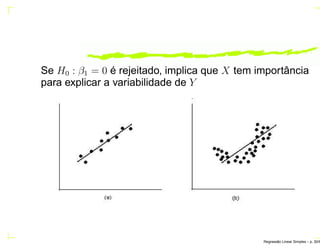
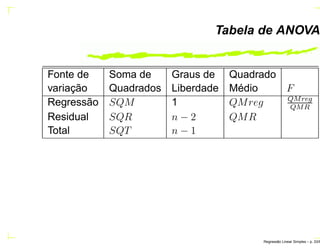
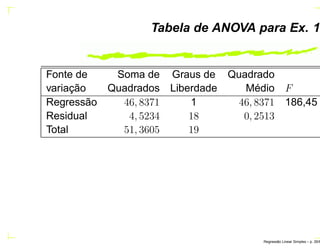
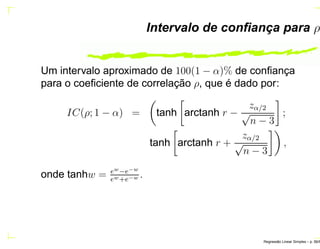
48. Intervalo de confiança para β0 e β1
Se para o MRLS é válida a suposição de que os
εi ∼ NID(0, σ2
), então
(ˆβ1 − β1)/ QMR/Sxx e (ˆβ0 − β0)/ QMR[
1
n
+
¯x2
Sxx
]
são variáveis aleatórias com distribuição t-Student com
n − 2 graus de liberdade.
Um intervalo de 100(1 − α)% de confiança para β1 :
IC(β1; 1−α) = ˆβ1 − tα
2
, n−2
QMR
Sxx
; ˆβ1 + tα
2
, n−2
QMR
Sxx
Regress˜ao Linear Simples – p. 36/6

49. De modo similar, um intervalo de 100(1 − α)% de confiança
para β0 é dado por:
IC(β0; 1 − α) = ˆβ0 − tα
2
, n−2 QMR[
1
n
+
¯x2
Sxx
]
ˆβ0 + tα
2
, n−2 QMR[
1
n
+
¯x2
Sxx
]
A seguir é obtido um intervalo de 95% de confiança para a
inclinação do MRLS com os dados do exemplo 1,
Regress˜ao Linear Simples – p. 37/6

50. Relembre que n = 20, ˆβ1 = 0, 00873, Sxx = 614, 603 e
QMR = 0, 2513. Para 1 − α = 0, 95, tem-se t0,025, 18 = 2, 101.
IC(β1; 0, 95) = (ˆβ1 − E ; ˆβ1 + E)
E = t0,025,18
QMR
Sxx
= 2, 101 0,2513
614.603
= 0, 00134
IC(β1; 0, 95) = (0, 00873 − 0, 00134; 0, 00873 + 0, 00134)
= (0, 00739; 0, 01007)
Regress˜ao Linear Simples – p. 38/6

51. Intervalo de confiança para resposta
média
O interesse consiste em estimar um intervalo de confiança
para
E(Y |X = x0) = µY |x0 = β0 + β1x0.
Um estimador pontual de µY |x0 é
ˆµY |xo = ˆY = ˆβ0 + ˆβ1x0.
Se εi ∼ NID(0, σ2
) é válida, pode-se demonstrar
T =
ˆµY |xo − µY |xo
QMR 1
n
+ (x0−¯x)2
Sxx
∼ t(n − 2)
Regress˜ao Linear Simples – p. 39/6

52. Int. conf. 100(1 − α)% para µY |x0
IC(ˆµY |x; 1 − α) = ˆµY |xo − E; ˆµY |xo + E
onde E = tα
2
, n−2 QMR[1
n
+ (x0−¯x)2
Sxx
]
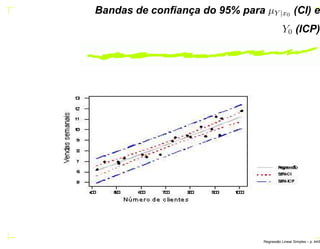
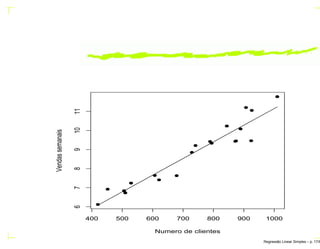
Exemplo: Suponha que tem-se interesse em construir um
intervalo de 95% de confiança da venda, média, semanal
para todos supermercados com 600 clientes.
Regress˜ao Linear Simples – p. 40/6

53. Int. conf. 100(1 − α)% para µY |x0
IC(ˆµY |x; 1 − α) = ˆµY |xo − E; ˆµY |xo + E
onde E = tα
2
, n−2 QMR[1
n
+ (x0−¯x)2
Sxx
]
Exemplo: Suponha que tem-se interesse em construir um
intervalo de 95% de confiança da venda, média, semanal
para todos supermercados com 600 clientes.
No modelo ajustado ˆµY |x0 = 2, 423 + 0, 00873x0. Para
x0 = 600, obtém-se ˆµY |x0 = 7, 661.
Regress˜ao Linear Simples – p. 40/6

54. Int. conf. 100(1 − α)% para µY |x0
IC(ˆµY |x; 1 − α) = ˆµY |xo − E; ˆµY |xo + E
onde E = tα
2
, n−2 QMR[1
n
+ (x0−¯x)2
Sxx
]
Exemplo: Suponha que tem-se interesse em construir um
intervalo de 95% de confiança da venda, média, semanal
para todos supermercados com 600 clientes.
No modelo ajustado ˆµY |x0 = 2, 423 + 0, 00873x0. Para
x0 = 600, obtém-se ˆµY |x0 = 7, 661. Também,
¯x = 731, 15, QMR = 0, 2513, Sxx = 614.603, n = 20
e 1 − α = 0, 95 ⇒ t0,05,18 = 2, 101.
Regress˜ao Linear Simples – p. 40/6

55. Int. conf. 100(1 − α)% para µY |x0
IC(ˆµY |x; 1 − α) = ˆµY |xo − E; ˆµY |xo + E
onde E = tα
2
, n−2 QMR[1
n
+ (x0−¯x)2
Sxx
]
Exemplo: Suponha que tem-se interesse em construir um
intervalo de 95% de confiança da venda, média, semanal
para todos supermercados com 600 clientes.
No modelo ajustado ˆµY |x0 = 2, 423 + 0, 00873x0. Para
x0 = 600, obtém-se ˆµY |x0 = 7, 661. Também,
¯x = 731, 15, QMR = 0, 2513, Sxx = 614.603, n = 20
e 1 − α = 0, 95 ⇒ t0,05,18 = 2, 101.
E = 2, 101 0, 2513[ 1
20
+ (600−731,15)2
614.603
] = 0, 292
Regress˜ao Linear Simples – p. 40/6

56. IC(µY |x0 ; 0, 95) = (7, 661 − 0, 292; 7, 661 + 0, 292)
= (7, 369; 7, 935)
Regress˜ao Linear Simples – p. 41/6

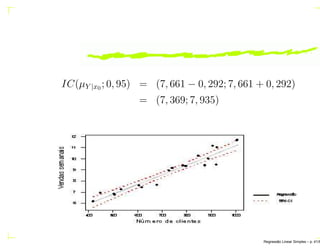
57. Previsão de novas observações
Uma aplicação muito importante de um modelo de
regressão é a previsão de novas ou futuras observações
de Y, (Y0) correspondente a um dado valor da variável
explicativa X, x0, então
ˆY0 = ˆβ0 + ˆβ1x0
é o melhor estimador pontual de Y0.
Um intervalo de 100(1 − α)% de confiança para uma futura
observação é dado por:
IC(Y0; 1 − α) = ( ˆY − E; ˆY + E)
onde E = tα
2
, n−2 QMR[1 + 1
n
+ (x0−¯x)2
Sxx
]
Regress˜ao Linear Simples – p. 42/6

58. Exemplo
Suponha agora, tem-se interesse em encontrar um
intervalo de previsão de 95% das vendas semanais de um
supermercado com 600 clientes.
Considerando os dados do exemplo 1, ˆY = 7, 661 e o
intervalo de predição é:
E = 2, 101 0, 2513[1 + 1
20
+ (600−731,15)2
614.603
] = 1, 084
IC(Y0; 0, 95) = (7, 661 − 1, 084; 7, 661 + 1, 084)
= (6, 577; 8, 745).
Regress˜ao Linear Simples – p. 43/6

59. Bandas de confiança do 95% para µY |x0 (CI) e
Y0 (ICP)
Regress˜ao Linear Simples – p. 44/6

60. Adequação do modelo de regressão
Análise residual,
Regress˜ao Linear Simples – p. 45/6

61. Adequação do modelo de regressão
Análise residual,
Coeficiente de determinação
Regress˜ao Linear Simples – p. 45/6

62. Adequação do modelo de regressão
Análise residual,
Coeficiente de determinação
Os resíduos de um modelo de regressão são definidos
como
ei = yi − ˆyi, i = 1, . . . , n
onde yi é uma observação real de Y e ˆyi é o valor
correspondente estimado através do modelo de regressão.
Regress˜ao Linear Simples – p. 45/6

63. Adequação do modelo de regressão
Análise residual,
Coeficiente de determinação
Os resíduos de um modelo de regressão são definidos
como
ei = yi − ˆyi, i = 1, . . . , n
onde yi é uma observação real de Y e ˆyi é o valor
correspondente estimado através do modelo de regressão.
Resíduos padronizados
di =
ei
√
QMR
, i = 1, . . . , n
Regress˜ao Linear Simples – p. 45/6

64. Adequação do modelo de regressão
Análise residual,
Coeficiente de determinação
Os resíduos de um modelo de regressão são definidos
como
ei = yi − ˆyi, i = 1, . . . , n
onde yi é uma observação real de Y e ˆyi é o valor
correspondente estimado através do modelo de regressão.
Resíduos padronizados
di =
ei
√
QMR
, i = 1, . . . , n
Regress˜ao Linear Simples – p. 45/6

65. Regress˜ao Linear Simples – p. 46/6

66. Gráfico de resíduos do exemplo 1
Regress˜ao Linear Simples – p. 47/6

67. Exemplo: Coeficiente de
Determinação
Para os dados dos supermercados do exemplo1,
determinar R2
.
Regress˜ao Linear Simples – p. 48/6

68. Exemplo: Coeficiente de
Determinação
Para os dados dos supermercados do exemplo1,
determinar R2
. Da definição tem-se:
R2
=
SQM
SQT
=
46, 8371
51, 3605
= 0, 912
Regress˜ao Linear Simples – p. 48/6

69. Exemplo: Coeficiente de
Determinação
Para os dados dos supermercados do exemplo1,
determinar R2
. Da definição tem-se:
R2
=
SQM
SQT
=
46, 8371
51, 3605
= 0, 912
Esse resultado significa que o modelo ajustado explicou
91,2% da variação na variável resposta Y (vendas
semanais). Isto é, 91,2% da variabilidade de Y é explicada
pela variável regressora X (número de clientes).
Regress˜ao Linear Simples – p. 48/6

70. Analise de Correlação
Suponha que se deseja desenvolver um modelo de
regressão que relacione a resistência ao corte dos pontos
de soldadura com o diâmetro dos mesmos. Neste caso,
não é possível controlar o diâmetro de soldadura. O que
pode ser feito é selecionar ao acaso n pontos de
soldadura e observar o diâmetro (Xi) e a resistência ao
corte (Yi) de cada um deles. Portanto, (Xi, Yi) são
variáveis aleatórias distribuídas de maneira conjunta.
Regress˜ao Linear Simples – p. 49/6

71. Suponha que a distribuição conjunta de Xi e Yi tenha uma
distribuição normal bivariada cuja função de densidade é
dada por
Regress˜ao Linear Simples – p. 50/6

72. Suponha que a distribuição conjunta de Xi e Yi tenha uma
distribuição normal bivariada cuja função de densidade é
dada por
f(x, y) =
1
2πσ1σ2 1 − ρ2
exp
1
2(1 − ρ2)
x − µ1
σ1
2
+
y − µ2
σ2
2
− 2ρ
x − µ1
σ1
y − µ2
σ2
Regress˜ao Linear Simples – p. 50/6

73. Suponha que a distribuição conjunta de Xi e Yi tenha uma
distribuição normal bivariada cuja função de densidade é
dada por
f(x, y) =
1
2πσ1σ2 1 − ρ2
exp
1
2(1 − ρ2)
x − µ1
σ1
2
+
y − µ2
σ2
2
− 2ρ
x − µ1
σ1
y − µ2
σ2
onde µ1 e σ2
1 são a média e variância de X e µ2 e σ2
2 são a
média e variância de Y e, ρ é coeficiente de correlac¸ ˜ao entre X
e Y.
Regress˜ao Linear Simples – p. 50/6

74. A densidade condicional de Y para um valor dado X = x é
dado por (exercicio 5.)
f(y|x) =
1
√
2πσY |x
exp



−
1
2
yi − β0 − β1x
σ2
Y |x
2



Regress˜ao Linear Simples – p. 51/6

75. A densidade condicional de Y para um valor dado X = x é
dado por (exercicio 5.)
f(y|x) =
1
√
2πσY |x
exp



−
1
2
yi − β0 − β1x
σ2
Y |x
2



onde β0 = µ2 − µ1ρσ2
σ1
, β1 = σ2
σ1
ρ e σ2
Y |x = σ2
2(1 − ρ2
)
Regress˜ao Linear Simples – p. 51/6

76. A densidade condicional de Y para um valor dado X = x é
dado por (exercicio 5.)
f(y|x) =
1
√
2πσY |x
exp



−
1
2
yi − β0 − β1x
σ2
Y |x
2



onde β0 = µ2 − µ1ρσ2
σ1
, β1 = σ2
σ1
ρ e σ2
Y |x = σ2
2(1 − ρ2
)
A distribuição condicional de Y dado X = x é normal com
média
E(Y |X = x) = β0 + β1x
e variância σ2
Y |x.
Regress˜ao Linear Simples – p. 51/6

77. Estimadores de β0, β1 e ρ
ˆβ0 = ¯Y − ˆβ1
¯X
Regress˜ao Linear Simples – p. 52/6

78. Estimadores de β0, β1 e ρ
ˆβ0 = ¯Y − ˆβ1
¯X
ˆβ1 =
Èn
i=1 Yi(Xi− ¯X)
Èn
i=1(Xi− ¯X)2 = SXY
SXX
Regress˜ao Linear Simples – p. 52/6

79. Estimadores de β0, β1 e ρ
ˆβ0 = ¯Y − ˆβ1
¯X
ˆβ1 =
Èn
i=1 Yi(Xi− ¯X)
Èn
i=1(Xi− ¯X)2 = SXY
SXX
ˆρ = r =
nÈ
i=1
Yi(Xi− ¯X)
× nÈ
i=1
(Xi− ¯X)2
nÈ
i=1
(Yi− ¯Y )2
= SXY√
SXX SY Y
Regress˜ao Linear Simples – p. 52/6

80. Estimadores de β0, β1 e ρ
ˆβ0 = ¯Y − ˆβ1
¯X
ˆβ1 =
Èn
i=1 Yi(Xi− ¯X)
Èn
i=1(Xi− ¯X)2 = SXY
SXX
ˆρ = r =
nÈ
i=1
Yi(Xi− ¯X)
× nÈ
i=1
(Xi− ¯X)2
nÈ
i=1
(Yi− ¯Y )2
= SXY√
SXX SY Y
ˆβ1 = SY Y
SXX
1/2
r
Regress˜ao Linear Simples – p. 52/6

81. Teste de hipóteses
H0 : ρ = 0 vs H1 : ρ = 0
A estatística de teste apropriada é
T =
r
√
n − 2
√
1 − r2
∼
sob H0 t(n − 2)
Regress˜ao Linear Simples – p. 53/6

82. Teste de hipóteses
H0 : ρ = 0 vs H1 : ρ = 0
A estatística de teste apropriada é
T =
r
√
n − 2
√
1 − r2
∼
sob H0 t(n − 2)
A hipótese nula deverá ser rejeitada se |Tobs| ≥ tα/2, n−2.
Esse teste é equivalente ao teste de hipóteses H0 : β1 = 0.
Regress˜ao Linear Simples – p. 53/6

83. H0 : ρ = ρ0 vs H1 : ρ = ρ0
onde ρ0 = 0.
Regress˜ao Linear Simples – p. 54/6

84. H0 : ρ = ρ0 vs H1 : ρ = ρ0
onde ρ0 = 0.
Para amostras de tamanho moderado grande (n ≥ 30), a
estatística
Regress˜ao Linear Simples – p. 54/6

85. H0 : ρ = ρ0 vs H1 : ρ = ρ0
onde ρ0 = 0.
Para amostras de tamanho moderado grande (n ≥ 30), a
estatística
Zr = arctanh r =
1
2
ln
1 + r
1 − r
tem distribuição aproximadamente normal com média
µZr = arctanh ρ =
1
2
ln
1 + ρ
1 − ρ
e variância σ2
Zr
= (n − 3)−1
.
Regress˜ao Linear Simples – p. 54/6

86. A estatística de teste apropriada é:
Z = (arctanh r − arctanh ρ0) (n − 3)1/2
.
Regress˜ao Linear Simples – p. 55/6

87. A estatística de teste apropriada é:
Z = (arctanh r − arctanh ρ0) (n − 3)1/2
.
Se H0 : ρ = ρ0 é verdadeira, a estatística Z tem,
aproximadamente, distribuição normal padrão. Portanto,
H0 deverá ser rejeitada se |Zobs| ≥ zα/2.
Regress˜ao Linear Simples – p. 55/6

88. Intervalo de confiança para ρ
Um intervalo aproximado de 100(1 − α)% de confiança
para o coeficiente de correlação ρ, que é dado por:
IC(ρ; 1 − α) = tanh arctanh r −
zα/2
√
n − 3
;
tanh arctanh r +
zα/2
√
n − 3
,
onde tanhw = ew−e−w
ew+e−w .
Regress˜ao Linear Simples – p. 56/6

89. Exemplo 2
Suponha que se tenha interesse em medir a força da
relação linear de dois produtos diferentes com relação ao
preço em várias cidades do mundo.
Y - Preço de uma libra de frango; e
X - Preço de uma caixa de suco.
Regress˜ao Linear Simples – p. 57/6

90. Caixa com seis Uma libra
Cidade sucos (X) de frango (Y )
Frankfurt 3,27 3,06
Hong Kong 2,22 2,34
Londres 2,28 2,27
Manila 3,04 1,51
México 2,33 1,87
Nova York 2,69 1,65
París 4,07 3,09
Sidney 2,78 2,36
Tokyo 5,97 4,85
Regress˜ao Linear Simples – p. 58/6

91. Dos dados da tabela são obtidos os valores seguintes:
n = 9;
n
i=1
Xi = 28, 65; ¯X = 3, 183;
n
i=1
X2
i = 28, 65 = 102
SXX = 11, 4594;
n
i=1
Yi = 23, 00; ¯Y = 2, 5566;
n
i=1
Y 2
i = 67
SY Y = 8, 3522;
n
i=1
XiYi = 81, 854; SXY = 8, 6437
r =
SXY
√
SXXSY Y
=
8, 6437
(11, 4594)(8, 3522)
= 0, 883.
Regress˜ao Linear Simples – p. 59/6

92. H0 : ρ = 0 (não relação linear entre X e Y )
H1 : ρ = 0 (há relação linear entre X e Y )
O valor calculado para a estatística do teste foi
Tobs =
r
√
n − 2
√
1 − r2
=
0, 883
√
9 − 2
1 − (0, 883)2
= 4, 98.
Para α = 0, 05, tem-se que t0,025,7 = 2, 365 < Tobs = 4, 98,
logo, rejeita-se H0 : ρ = 0 ao nível de significância de
α = 5%.
Regress˜ao Linear Simples – p. 60/6