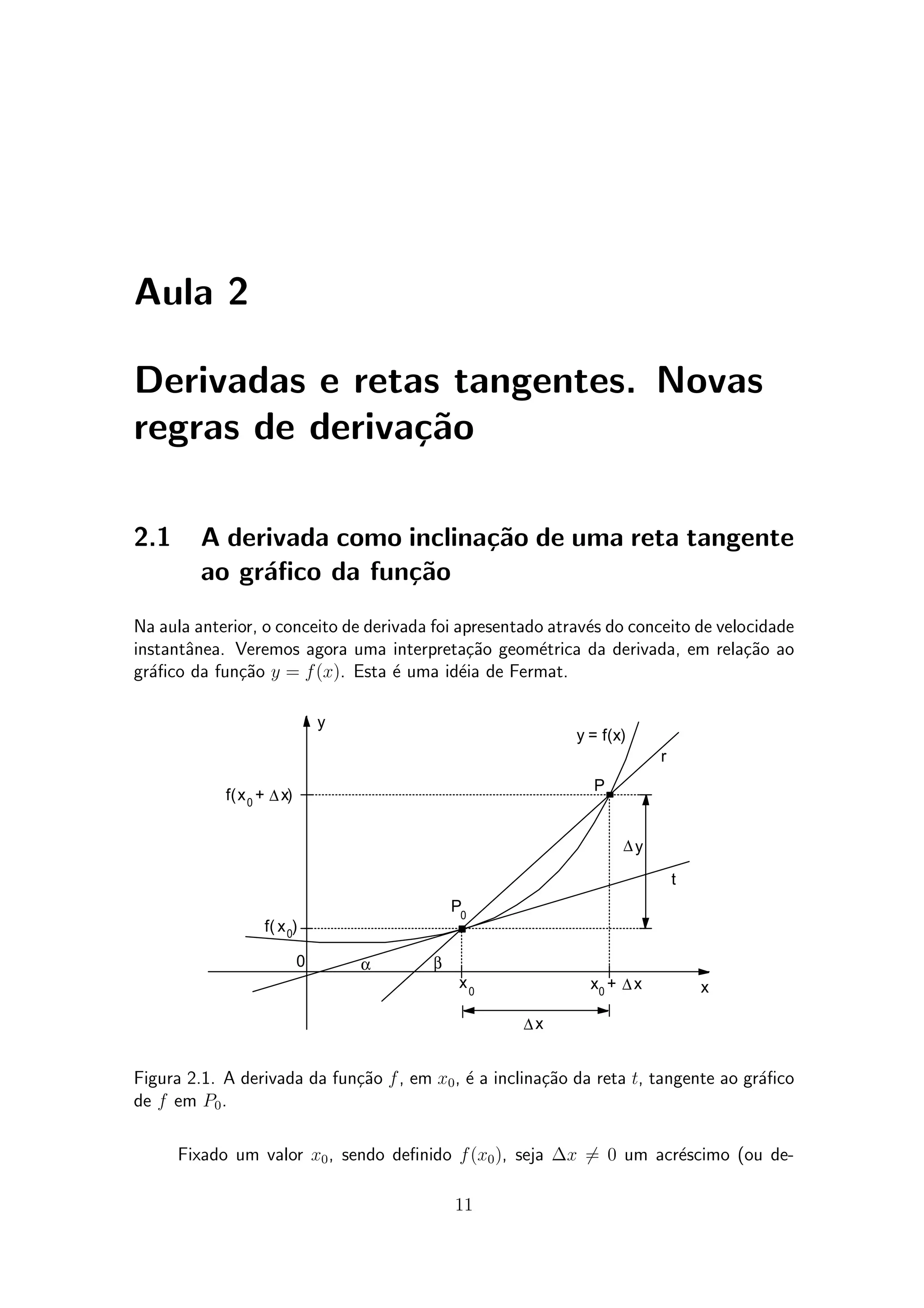
O documento apresenta as noções de derivada como inclinação da reta tangente ao gráfico de uma função e novas regras de derivação, como a derivada de um produto e a derivada da inversa de uma função. É introduzido o conceito geométrico de derivada ligado à aproximação linear local de uma função por sua tangente e são mostradas equações de retas tangentes e normais a curvas.

1. Aula 2
Derivadas e retas tangentes. Novas
regras de deriva»~o
ca
2.1 A derivada como inclina»~o de uma reta tangente
ca
ao gr¶¯co da fun»~o
a ca
Na aula anterior, o conceito de derivada foi apresentado atrav¶s do conceito de velocidade
e
instant^nea. Veremos agora uma interpreta»~o geom¶trica da derivada, em rela»~o ao
a ca e ca
gr¶¯co da fun»~o y = f (x). Esta ¶ uma id¶ia de Fermat.
a ca e e
y
y = f(x)
r
P
f( x 0 + ∆ x)
∆y
t
P0
f( x 0)
0 α β
x0 x0 + ∆ x x
∆x
Figura 2.1. A derivada da fun»~o f , em x0 , ¶ a inclina»~o da reta t, tangente ao gr¶¯co
ca e ca a
de f em P0 .
Fixado um valor x0 , sendo de¯nido f (x0 ), seja ¢x 60 um acr¶scimo (ou de-
= e
11

2. »~
Derivadas e retas tangentes. Novas regras de derivacao 12
cr¶scimo) dado a x0 . Sendo x1 = x0 + ¢x, temos que a raz~o
e a
¢y f (x0 + ¢x) ¡ f (x0 ) f(x1 ) ¡ f (x0 )
= =
¢x ¢x x1 ¡ x0
¶ o coe¯ciente angular da reta r, secante ao gr¶¯co da curva y = f (x), passando pelos
e a
pontos P0 = (x0 ; f(x0 )) e P = (x1 ; f(x1 )).
Observando os elementos geom¶tricos da ¯gura 2.1, temos que quando ¢x tende
e
a 0, o ponto P tem como posi»~o limite o ponto P0 , e a reta secante P0 P ter¶ como
ca a
posi»~o limite a reta t, tangente ao gr¶¯co de f no ponto P0 .
ca a
Na ¯gura, temos ainda, da geometria anal¶
³tica elementar,
tg ¯ = tangente do ^ngulo ¯
a
= coe¯ciente angular (ou inclina»~o) da reta secante P0 P
ca
¢y
= :
¢x
tg ® = tangente do ^ngulo ®
a
= coe¯ciente angular da reta t, tangente ao gr¶¯co de f , no ponto P0 :
a
Note aqui diferentes empregos (com diferentes signi¯cados) da palavra tangente: a tan-
gente (trigonom¶trica) do ^ngulo ®, nos d¶ a inclina»~o, ou declividade, ou coe¯ciente
e a a ca
angular, da reta t, que ¶ (geometricamente) tangente ao gr¶¯co de f (ou que tangencia
e a
o gr¶¯co de f) no ponto P0 .
a
¢y
Quando ¢x tende a 0, ¯ tende a ®, e ent~o
a ¢x
= tg ¯ tende a tg ®.
¢y
Da¶ lim
³, = tg ®.
¢x!0 ¢x
Assim, com este argumento geom¶trico e intuitivo, interpretamos f 0 (x0 ) = tg ® como
e
sendo o coe¯ciente angular (ou a inclina»~o) da reta t, tangente ao gr¶¯co de f (ou
ca a
seja, tangente µ curva y = f (x)) no ponto P0 = (x0 ; f (x0 )).
a
Sabemos que a equa»~o de uma reta, de coe¯ciente angular m, passando por um
ca
ponto P0 = (x0 ; y0 ), ¶ dada por
e
y ¡ y0 = m(x ¡ x0 ):
Assim sendo, temos que a equa»~o da reta t, tangente µ curva y = f (x) no ponto
ca a
P0 = (x0 ; y0 ) = (x0 ; f (x0 )) ¶ dada por
e
y ¡ y0 = f 0 (x0 ) ¢ (x ¡ x0 )
Em geral, se queremos aproximar a fun»~o f (x), nas proximidades de x0 , por uma
ca
fun»~o da forma g(x) = ax + b, tomamos g(x) = f(x0 ) + f 0 (x0 ) ¢ (x ¡ x0 ). O gr¶¯co
ca a

3. »~
Derivadas e retas tangentes. Novas regras de derivacao 13
de g ser¶ ent~o a reta tangente ao gr¶¯co de f no ponto P0 . Dizemos que g(x) ¶ uma
a a a e
lineariza»~o de f (x) nas proximidades de x0 .
ca
A reta normal µ curva y = f(x), no ponto P0 dessa curva, ¶ a reta que passa por
a e
P0 perpendicularmente µ curva. Isto, ¶, r ¶ normal µ curva y = f (x), no ponto P0 ,
a e e a
quando r ¶ perpendicular µ reta tangente µ curva nesse ponto.
e a a
Lembre-se que se duas retas s~o perpendiculares, tendo coe¯cientes angulares m
a
0 0
e m , ent~o m = ¡1=m.
a
Assim, se f 0 (x0 ) 6 0, a equa»~o da reta r, normal µ curva y = f (x) no ponto
= ca a
P0 = (x0 ; y0 ) ¶
e
1
y ¡ y0 = ¡ 0 (x ¡ x0 )
f (x0 )
Exemplo 2.1 Qual ¶ a equa»~o da reta t, que tangencia a par¶bola y = x2 , no ponto
e ca a
P = (¡1; 1)? Qual ¶ a equa»~o da reta r, normal µ par¶bola nesse ponto?
e ca a a
y
t
r
P 1
-1 1 x
-1
Figura 2.2. Representa»~o gr¶¯ca da curva y = x2 e das retas t e r, tangente e normal
ca a
µ curva no ponto P = (¡1; 1).
a
dy
Solu»~o. Sendo y = x2 , temos
ca = 2x. Em P , temos x0 = ¡1. O coe¯ciente
dx
angular da reta t ¶ dado por
e
¯
dy ¯
¯ = 2 ¢ (¡1) = ¡2:
dx ¯x=¡1

4. »~
Derivadas e retas tangentes. Novas regras de derivacao 14
Assim, a reta t, tangente µ curva y = x2 no ponto P , tem equa»~o
a ca
y ¡ 1 = (¡2)(x ¡ (¡1))
ou seja, y = ¡2x ¡ 1.
Para escrever a equa»~o da reta r, normal µ curva no ponto P , fazemos uso do
ca a
fato de que a declividade da reta r ¶ mr = ¡ mt = 1 .
e 1
2
Portanto, r tem equa»~o y ¡ 1 = 1 (x + 1), ou ainda y = 1 x + 3 .
ca 2 2 2
Na ¯gura 2.2 temos a representa»~o da curva y = x2 e das retas t e r, respecti-
ca
vamente tangente e normal µ curva no ponto P = (¡1; 1).
a
Exemplo 2.2 Determine o coe¯ciente angular da reta tangente ao gr¶¯co de y =
a
2
f (x) = x ¡ 4x, no ponto de abscissa (primeira coordenada) p. Em qual ponto a reta
tangente ao gr¶¯co ¶ horizontal?
a e
Solu»~o. O coe¯ciente angular da reta tangente µ curva y = x2 ¡ 4x, no ponto
ca a
0 0
de abscissa p, ¶ m = f (p). Como f (x) = 2x ¡ 4, temos m = 2p ¡ 4.
e
No ponto (p; f(p)) em que a reta tangente ¶ horizontal, temos m = 0, ou seja,
e
f 0 (p) = 0. Logo, p = 2. Assim, o ponto procurado ¶ (2; ¡4).
e
2.2 Novas regras de deriva»~o
ca
Regra 2.1 (Derivada de um produto)
(f g)0 = f 0 g + f g 0
Demonstra»~o. Temos
ca
¢f = f(x + ¢x) ¡ f (x), ¢g = g(x + ¢x) ¡ g(x).
Portanto
f (x + ¢x) = f (x) + ¢f , g(x + ¢x) = g(x) + ¢g.
Assim sendo
¢(f g) = f(x + ¢x)g(x + ¢x) ¡ f(x)g(x)
= (f(x) + ¢f )(g(x) + ¢g) ¡ f(x)g(x)
= f(x)g(x) + f (x)(¢g) + (¢f )g(x) + (¢f )(¢g) ¡ f(x)g(x)
= f(x)(¢g) + (¢f )g(x) + (¢f )(¢g)
Portanto

5. »~
Derivadas e retas tangentes. Novas regras de derivacao 15
¢(f g) ¢g ¢f ¢f
= f(x) + g(x) + (¢g)
¢x ¢x ¢x ¢x
¢g ¢f ¢f ¢g
= f(x) + g(x) + ¢x
¢x ¢x ¢x ¢x
E assim,
µ ¶
¢(fg) ¢g ¢f ¢f ¢g
lim = lim f (x) + g(x) + ¢x
¢x!0 ¢x ¢x!0 ¢x ¢x ¢x ¢x
= f (x)g 0 (x) + f 0 (x)g(x) + f 0 (x)g 0 (x) ¢ 0
= f 0 (x)g(x) + g 0 (x)f (x)
Portanto, (f (x)g(x))0 = f 0 (x)g(x) + f(x)g 0 (x).
³¯co de x, digamos x = x0 , temos
Observa»~o 2.1 Para um valor espec¶
ca
¢f = f(x0 + ¢x) ¡ f(x0 ).
Embora n~o tenhamos ainda mencionado, ¶ fato que se podemos calcular o limite
a e
lim ¢f 0
= f (x0 ), ent~o temos lim ¢f = 0.
a
¢x!0 ¢x ¢x!0
De fato,
¢f
lim ¢f = lim ¢ ¢x = f 0 (x0 ) ¢ 0 = 0:
¢x!0 ¢x!0 ¢x
Exemplo 2.3 Daremos um exemplo para ilustrar a regra da derivada de um produto,
que acabamos de deduzir. Considere p(x) = (x2 + x + 2)(3x ¡ 1)
Expandindo p(x), obtemos p(x) = 3x3 + 2x2 + 5x ¡ 2, de onde obtemos p0 (x) =
2
9x + 4x + 5.
Por outro lado, se aplicarmos a f¶rmula da derivada de um produto, obtemos
o
p0 (x) = (x2 + x + 2)0 (3x ¡ 1) + (x2 + x + 2)(3x ¡ 1)0
= (2x + 1)(3x ¡ 1) + (x2 + x + 2) ¢ 3
= 9x2 + 4x + 5
Regra 2.2 Sendo g uma fun»~o deriv¶vel, quando g 60 temos
ca a =
µ ¶0
1 g0
= ¡ 2:
g g
Demonstra»~o. Como na dedu»~o da propriedade 2.1, temos g(x + ¢x) = g(x) + ¢g.
ca ca

6. »~
Derivadas e retas tangentes. Novas regras de derivacao 16
Sendo y = 1=g(x), temos
1 1
¢y = ¡
g(x + ¢x) g(x)
1 1
= ¡
g(x) + ¢g g(x)
g(x) ¡ (g(x) + ¢g)
=
(g(x) + ¢g) ¢ g(x)
¡¢g
=
(g(x) + ¢g) ¢ g(x)
Logo,
¢y ¡¢g 1
= ¢
¢x ¢x (g(x) + ¢g)g(x)
e portanto
dy ¢y
= lim
dx ¢x!0 ¢x
¡¢g 1
= lim ¢
¢x!0 ¢x (g(x) + ¢g)g(x)
1 g 0 (x)
= ¡g 0 (x) ¢ =¡
(g(x))2 (g(x))2
Aqui, ¯zemos uso da observa»~o 2.1: sendo g deriv¶vel, temos lim ¢g = 0.
ca a
¢x!0
Exemplo 2.4 Veri¯que que, sendo n um inteiro positivo, (x¡n )0 = ¡nx¡n¡1 .
Solu»~o. Aplicando o resultado da propriedade 2.2, temos
ca
µ ¶0
¡n 0 1 (xn )0 nxn¡1
(x ) = = ¡ n 2 = ¡ 2n = ¡nx¡n¡1
xn (x ) x
Regra 2.3 (Derivada de um quociente)
µ ¶0
f f 0g ¡ f g0
=
g g2
Demonstra»~o.
ca Deixamos a dedu»~o desta regra para o leitor. Para deduzi-la, basta
ca
f 1
escrever = f ¢ e ent~o combinar as regras (propriedades) 2.1 e 2.2.
a
g g
x3 ¡ 1
Exemplo 2.5 Calcular y 0 , sendo y =
x3 + 1

7. »~
Derivadas e retas tangentes. Novas regras de derivacao 17
Solu»~o. Aplicando a f¶rmula para a derivada de um quociente, temos
ca o
µ 3 ¶0
0 x ¡1 (x3 ¡ 1)0 (x3 + 1) ¡ (x3 + 1)0 (x3 ¡ 1)
y = =
x3 + 1 (x3 + 1)2
3x2 (x3 + 1) ¡ 3x2 (x3 ¡ 1)
=
(x3 + 1)2
6x2
= 3
(x + 1)2
2.3 Problemas
1. Utilizando regras de deriva»~o previamente estabelecidas, calcule as derivadas das
ca
seguintes fun»~es.
co
4x ¡ 5
(a) f(x) =
3x + 2
8 ¡ z + 3z 2
(b) f(z) =
2 ¡ 9z
2w
(c) f(w) = 3
w ¡7
1
(d) s(t) = t2 + 2
t
1
(e) f(x) =
1 + x + x2 + x3
x2 + 9x + 2
(f) f(x) =
7
2. Deduza a seguinte f¶rmula de deriva»~o:
o ca
(f gh)0 = f 0 gh + f g 0 h + f gh0
D^ um bom palpite (chute) sobre como seria a f¶rmula para (f1 f2 ¢ ¢ ¢ fn¡1 fn )0 .
e o
5
3. Ache as equa»~es das retas tangentes ao gr¶¯co de y =
co a , nos pontos
1 + x2
P = (0; 5), Q = (1; 5=2) e R = (¡2; 1). Esboce (caprichadamente) o gr¶¯co a
dessa curva, plotando pontos com os seguintes valores de x: ¡3, ¡2, ¡1, 0, 1,
2 e 3. No mesmo sistema cartesiano, esboce tamb¶m as retas tangentes µ curva
e a
nos pontos P , Q e R.
4. Escreva as equa»~es das retas tangente e normal µ curva y = x3 ¡ 3x2 ¡ x + 5
co a
no ponto de abcissa x = 3.
5. Determine as equa»~es das retas t e n, respectivamente tangente e normal µ curva
co a
2
y = x , no ponto de abcissa p.

8. »~
Derivadas e retas tangentes. Novas regras de derivacao 18
6. (Teste sua sensibilidade sobre derivadas) Esboce o gr¶¯co de y = x2 ¡ 4, plotando
a
os pontos de abcissas (valores de x) ¡2, ¡1, 0, 1, 2 e 3. Em cada um desses
pontos, esboce a reta tangente ao gr¶¯co, e tente adivinhar o seu coe¯ciente
a
angular. Marque seu chute ao lado do ponto. Em seguida, calcule cada coe¯ciente
angular usando a derivada y 0 . Compare seu chute com a resposta exata.
2.3.1 Respostas e sugest~es
o
23
1. (a) f 0 (x) =
(3x + 2)2
¡27z 2 + 12z + 70
(b) f 0 (z) =
(2 ¡ 9z)2
¡4w3 ¡ 14
(c) f 0 (w) =
(w3 ¡ 7)2
2
(d) s0 (t) = 2t ¡ 3
t
1 + 2x + 3x2
(e) f 0 (x) = ¡
(1 + x + x2 + x3 )2
2x + 9 ³ ´0
f0
(f) f 0 (x) = (Quando c ¶ uma constante, temos a regra f =
e c c)
7
2. (f1 f2 ¢ ¢ ¢ fn¡1 fn )0 = f1 f2 ¢ ¢ ¢ fn¡1 fn + f1 f2 ¢ ¢ ¢ fn¡1 fn + ¢ ¢ ¢ + f1 f2 ¢ ¢ ¢ fn¡1 fn +
0 0 0
0.
f1 f2 ¢ ¢ ¢ fn¡1 fn
3. As equa»~es das tr^s retas s~o, respectivamente, y = 5, 5x+2y¡10 = 0, e 4x¡5y+13 =
co e a
0.
4. Reta tangente: y = 8x ¡ 22. Reta normal: x + 8y ¡ 19 = 0.
5. t : y = 2px ¡ p2 ;
x 1
n : y = ¡ + + p2 (se p 60); n : x = 0 (se p = 0).
=
2p 2