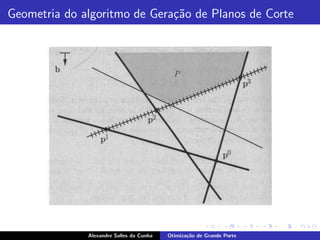
O documento descreve algoritmos de otimização para problemas de grande porte, como o problema de cortes unidimensional. Ele apresenta formulações de Kantorovich, Gilmore e Gomory para o problema, além de explicar o método de geração de colunas para resolver as formulações de forma implícita evitando enumerar todas as colunas. O documento também discute a geração de planos de corte aplicando o método de geração de colunas ao dual do problema.

1. Otimiza¸˜o de Grande Porte
ca
Alexandre Salles da Cunha
DCC-UFMG, Maio 2010
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

2. Escopo do Cap´
ıtulo
Gera¸˜o de Colunas
ca
Princ´ de Decomposi¸˜o de Dantzig-Wolfe
ıpio ca
Aplica¸˜o em do Princ´ em PL
ca ıpio
Aplica¸˜o de CG e DW em Programa¸˜o Inteira
ca ca
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

3. O Problema de Cortes Unidimensional
Dados do problema:
Uma quantidade irrestrita (t˜o grande quanto queiramos) de bobinas
a
de papel de largura W e altura H.
Um conjunto de m perfis de tiras de papel.
Cada perfil possui altura H (a mesma altura da bobina) e largura
wi ∈ Z+ , wi ≤ W .
Demandas bi ∈ Z+ associadas a cada perfil i de tiras de papel.
Objetivo
Cortar bobinas de forma a atender a demanda de cada perfil de tiras de
papel, de forma que o n´mero de bobinas cortadas seja o menor poss´
u ıvel.
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

4. Formula¸˜o de Kantorovich (1960)
ca
Seja K um limite superior para o n´mero m´
u ınimo de bobinas a serem
cortadas, por exemplo, K = m ⌈ j bi k ⌉
i W
wi
Vari´veis de decis˜o:
a a
◮ xik ∈ Z+ indicando quantos perfils i s˜o cortados na k−´sima bobina.
a e
◮ y k ∈ B assumindo valor 1 caso a k−´sima bobina seja usada (0, cc)
e
K
min yk (1)
k=1
K
xik ≥ bi ∀i (2)
k=1
m
wi xik ≤ Wy k ∀k (3)
i =1
k
xk ∈ Z + ∀k, i (4)
j
y ∈B ∀k (5)
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

5. Formula¸˜o de Gilmore e Gomory (1961)
ca
Defini¸˜o - padr˜o de corte
ca a
Dizemos que um padr˜o (pattern) de corte j ´ um modo v´lido de cortar a
a e a
bobina de largura W se a restri¸˜o da Mochila Inteira:
ca
m
aij wi ≤ W
i =1
onde aij denota a quantidade de perfis do tipo i cortados no padr˜o j. As
a
sobras do padr˜o de corte n˜o s˜o reaproveitadas.
a a a
Vamos assumir que:
P denota o conjunto de todos os poss´
ıveis padr˜es de corte vi´veis e
o a
que |P| = n.
O vetor m dimensional de entradas inteiras Aj denota o n´mero de
u
perfis de cada tipo cortados no padr˜o j ∈ P.
a
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

6. Formula¸˜o de Gilmore e Gomory (1961)
ca
Vari´vel de decis˜o: xj ∈ Z+ que representa o n´mero de vezes que o
a a u
perfil j ∈ P for empregado.
n
min xj (6)
j=1
n
Aj xj = bi i = 1, . . . , m (7)
j=1
xj ∈ Z j = 1, . . . , n (8)
Esta formula¸˜o compreende m restri¸˜es e um n´mero
ca co u
exponencialmente grande de vari´veis de decis˜o (colunas).
a a
Assim sendo ´ impratic´vel resolver o problema atrav´s de um m´todo
e a e e
que use explicitamente todas as colunas da formula¸˜o.
ca
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

7. Como se utiliza a formula¸˜o anterior ?
ca
Relaxamos a integralidade das restri¸˜es, substituindo xj ∈ Z+ por
co
xj ≥ 0.
Resolvemos o Problema de Programa¸˜o Linear associado, obtendo-se
ca
limites de Relaxa¸˜o Linear que ser˜o usados em um procedimento
ca a
enumerativo do tipo Branch-and-bound (na verdade s˜o chamados de
a
Branch-and-price).
Para resolver a Relaxa¸˜o Linear da formula¸˜o, precisamos usar as
ca ca
colunas implicitamente e n˜o explicitamente, atrav´s do procedimento
a e
de Gera¸˜o de Colunas.
ca
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

8. Gera¸˜o de Colunas
ca
Vamos considerar o PL (Master Restrito):
min xj (9)
j∈P
Aj xj = bi i = 1, . . . , m (10)
j∈P
xj ≥ 0 j ∈P (11)
onde P ⊆ P : |P| << |P|.
Exemplo: fazemos cada padr˜o de P ser exatamente equivalente ao
a
corte de um unico perfil i (|P| = m).
´
Vamos assumir que uma solu¸˜o b´sica vi´vel para o PL acima seja
ca a a
poss´ de ser encontrada. No caso da escolha de P acima ´ claro
ıvel e
que xj = bi ´ uma solu¸˜o b´sica vi´vel.
e ca a a
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

9. Gera¸˜o de Colunas
ca
Resolvemos o Programa Linear dado pelo Master Restrito (definido a
partir de P) atrav´s do M´todo Simplex, obtendo uma solu¸˜o b´sica
e e ca a
vi´vel associada a uma base B e o valor zP para o seu m´
a ınimo.
Para garantir que zP seja o valor do ´timo do Programa Linear
o
Original (Master), precisamos garantir que n˜o existam colunas
a
atrativas n˜o inclu´
a ıdas em P.
Para decidir sobre esta quest˜o, precisamos verificar se existe coluna
a
j ∈ P P que possua custo reduzido c j = 1 − p ′ Aj < 0, onde
p ′ = cB B −1 ´ o vetor de vari´veis duais ´timas.
′ e a o
Como determinar se existe j : c j < 0 sem enumerar todas as colunas ?
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

10. Resolvendo o Problema de Precifica¸˜o
ca
Ao inv´s de enumerar todas as colunas e calcular c j , formulamos um
e
Problema de Otimiza¸˜o que nos permite decidir sobre a existˆncia de
ca e
j : c j < 0.
Formulamos e resolvemos o Problema de Precifica¸˜o max p ′ Aj para
ca
todo j (recorde que Aj = (a1j , . . . , amj )′ )
Neste caso, o Problema de Precifica¸˜o consiste no Problema da
ca
Mochila Inteira:
m
max pi aij (12)
i =1
m
aij wi ≤ W (13)
i =1
aij ∈ Z+ (14)
que pode ser resolvido em tempo pseudo polinomial O(mW ) atrav´s
e
de Programa¸˜o Dinˆmica.
ca a
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

11. O M´todo de Gera¸˜o de colunas
e ca
Vamos assumir que o Problema de Precica¸˜o tenha sido resolvido e
ca
que o perfil k ∈ P seja sua solu¸˜o ´tima.
ca o
Se ck = 1 − m pi aki < 0, a coluna k deve ser introduzida no
i =1
modelo. Neste caso, fazemos P ← P ∪ {k}, redefinindo um novo
Problema Master Restrito, que ´ reotimizado e o procedimento se
e
repete, dando origem a uma nova itera¸˜o do M´todo de Gera¸˜o de
ca e ca
Colunas.
Caso contr´rio, se ck = 1 − m pi aki ≥ 0, o valor do Programa
a i =1
Master Restrito corresponde ` solu¸˜o ´tima da Relaxa¸˜o Linear do
a ca o ca
problema de corte unidimensional. Al´m disto, a solu¸˜o b´sica ´tima
e ca a o
do Master restrito ´ uma solu¸˜o b´sica ´tima do Programa Master.
e ca a o
Podemos adotar v´rios crit´rios para descartar ou n˜o vari´veis
a e a a
(colunas) em P ao longo de cada itera¸˜o do M´todo.
ca e
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

12. Gera¸˜o de Planos de Corte
ca
Vamos considerar o Programa Linear Master e seu Dual:
n
m
min xj
j=1
max pi bi
n i =1
m
Aj xj = bi , i = 1, . . . , m
pi aij , ≤ cj j = 1, . . . , n
j=1
i =1
xj ≥ 0 j = 1, . . . , n
Ao inv´s de resolver o Dual, vamos resolver uma relaxa¸˜o para o
e ca
Dual, escrito em termos apenas de um conjunto P de restri¸˜es:
co
m
max pi bi
i =1
m
pi aij , ≤ cj j ∈ P
i =1
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

13. Gera¸˜o de Planos de Corte
ca
Considerando que o Dual Relaxado foi resolvido e que obtivemos p ∗ como
sua solu¸˜o ´tima, temos duas possibilidades:
ca o
Caso 1 - p ∗ ´ uma solu¸˜o vi´vel para o problema dual original. Neste
e ca a
caso, p ∗ tamb´m ´ solu¸˜o ´tima para o problema dual original,
e e ca o
porque qualquer solu¸˜o p deste ´ vi´vel para o relaxado e ent˜o:
ca e a a
p ′ b ≤ (p ∗ )′ b.
Caso 2 - p ∗ ´ invi´vel para o problema dual original. Neste caso,
e a
existe uma restri¸˜o dual violada por p ∗ . Identificamos esta restri¸˜o,
ca ca
introduzimos a mesma no dual Relaxado e reotimizamos.
Para proceder com este algoritmo, precisamos resolver o Problema de
Separa¸˜o que consiste em identificar uma restri¸˜o dual violada ou
ca ca
garantir que restri¸˜es violadas n˜o existam.
co a
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

14. Gera¸˜o de Colunas
ca
O Problema de Separa¸˜o
ca
min cj − (p ∗ )′ Aj
j∈P
Se o valor ´timo deste Programa Linear, obtido para a restri¸˜o k, ´
o ca e
n˜o negativo, garantimos que p ∗ ´ vi´vel para o Problema Dual
a e a
Original.
Caso contr´rio, se ck < (p ∗ )Ak para a coluna que resolveu o
a
Problema de Separa¸˜o, introduzimos a correspondente restri¸˜o no
ca ca
Dual Relaxado, fazendo P ← P ∪ {k}
Aplicar o algoritmo de Gera¸˜o de Colunas no Problema Primal equivale a
ca
aplicar o algoritmo de Gera¸˜o de Planos de Cortes no seu dual.
ca
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

15. Geometria do algoritmo de Gera¸˜o de Planos de Corte
ca
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

16. Decomposi¸˜o de Dantzig-Wolfe
ca
Vamos considerar o seguinte Programa Linear com estrutura:
′ ′
min c1 x1 + c2 x2
D 1 x1 + D 2 x2 = b0
F 1 x1 = b1
F 2 x2 = b2
x1 , x2 ≥ 0
onde x1 , x2 , b0 , b1 , b2 s˜o vetores de dimens˜es n1 , n2 , m0 , m1 , m2 ,
a o
respectivamente e as matrizes D1 , D2 , F1 , F2 possuem dimens˜es o
apropriadas.
Observe que:
as primeiras m0 restri¸˜es fazem o acoplamento dos vetores x1 , x2
co
os sistemas F1 x1 = b1 , F2 x2 = b2 s˜o independentes de x2 , x1
a
respectivamente.
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

17. Reformulando o Problema
Vamos considerar os seguintes poliedros:
Pi = {xi ∈ Rni : Fi xi = bi }
+
e assumir que Pi : i = 1, 2 s˜o n˜o vazios.
a a
Podemos ent˜o reescrever o Programa Linear da seguinte forma:
a
′ ′
min c1 x1 + c2 x2
D 1 x 1 + D 2 x 2 = b0
x1 ∈ P1
x2 ∈ P2
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

18. Reformulando o Problema
Vamos considerar ent˜o que {xij : j ∈ Ji } denota o conjunto de
a
pontos extremos do poliedro Pi : i = 1, 2.
De modo similar, vamos considerar que {wik : k ∈ Ki } denota o
conjunto de raios extremos de Pi : i = 1, 2.
Observe ent˜o que pelo Teorema de Minkowski, um ponto qualquer
a
xi ∈ Pi : i = 1, 2 pode ser escrito como:
xi = λj xij +
i θik wik
j∈Ji k∈Ki
λj = 1
i
j∈Ji
λij ≥ 0, j ∈ Ji
θik ≥ 0, k ∈ Ki
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

19. Reformulando o Problema
Problema Master:
min λj c1 x1 +
1
′ j
k∈K1
k ′ k
θ1 c1 w1 + λj c2 x2 +
2
′ j k ′ k
θ2 c2 w2
j∈J1 j∈J2 k∈K2
λj D 1 x 1 +
1
j
k∈K1
k k
θ1 D1 w1 + λj D2 x2 +
2
j k k
θ2 D2 w2 = b0
j∈J1 j∈J2 k∈K2
λj = 1
1
j∈J1
λj = 1
2
j∈J2
λij ≥ 0 j ∈ Ji , i = 1, 2
θik ≥ 0 k ∈ Ki , i = 1, 2
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

20. Reformulando o problema
Na forma matricial, o conjunto de restri¸˜es do Problema Master fica:
co
j j
2 3 2 3 2 k
3 2 k
3 2 3
D1 x 1 D2 x 2 D1 w1 D2 w2 b0
λj
X X j X X
k 4 k 4
1
4 1 5+ λ2 4 0 5+ θ1 0 5+ θ2 0 5=4 1 5
j∈J1 0 j∈J2 1 k∈K1 0 k∈K2 0 1
Observe que, diferentemente do Programa Linear Original que possuia
m0 + m1 + m2 restri¸˜es, o Programa Reformulado possui apenas
co
m0 + 2 linhas.
Uma base para este programa deve envolver ter dimens˜o m0 + 2.
a
Por outro lado, o novo programa possui |J1 | + |J2 | + |K1 | + |K2 |
vari´veis.
a
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

21. O algoritmo de Decomposi¸˜o
ca
Vamos assumir que dispomos de um conjunto de colunas inicial, isto ´, e
subconjuntos J 1 , J 2 , K 1 , K 2 que nos permita resolver e obter uma solu¸˜o
ca
b´sica vi´vel para o Programa Master Restrito:
a a
min λj c1 x1 +
1
′ j
k∈K 1
k ′ k
θ1 c1 w1 + λj c2 x2 +
2
′ j k ′ k
θ2 c2 w2
j∈J 1 j∈J 2 k∈K 2
λj D 1 x 1 +
1
j
k∈K 1
k k
θ1 D1 w1 + λj D 2 x 2 +
2
j k k
θ2 D2 w2 = b0
j∈J 1 j∈J 2 k∈K 2
λj
1 =1
j∈J 1
λj = 1
2
j∈J 2
λj ≥ 0
i j ∈ J i , i = 1, 2
θik ≥ 0 k ∈ K i , i = 1, 2
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

22. O algoritmo de Decomposi¸˜o
ca
Assumimos ent˜o que B denote a matriz b´sica associada ao
a a
Programa Master Restrito, resolvido ` otimalidade.
a
Seja p ′ = cB B −1 o vetor m0 + 2 dimensional de vari´veis duais
′ a
o
´timas, do Programa Dual do Master Restrito.
Vamos dizer que p = (q, r1 , r2 ), onde r1 e r2 s˜o as vari´veis duais
a a
associadas `s restri¸˜es de convexidade.
a co
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

23. O algoritmo de Decomposi¸˜o
ca
Custos reduzidos
Os custos reduzidos de uma vari´vel λj s˜o dados por
a 1 a
 j 
D 1 x1
′ j j
 1  = (c1 − q ′ D1 )x1 − r1
′
c1 x1 − q ′ r1 r2
0
k a
Os custos reduzidos de uma vari´vel θ1 s˜o dados por
a
 j 
D1 w1
′ j j
 0  = (c1 − q ′ D1 )w1
′
c1 w1 − q ′ r1 r2
0
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

24. O algoritmo de Decomposi¸˜o
ca
Custos reduzidos
Os custos reduzidos de uma vari´vel λj s˜o dados por
a 2 a
 j 
D 2 x2
′ j j
 0  = (c2 − q ′ D2 )x2 − r2
′
c2 x2 − q ′ r1 r2
1
k a
Os custos reduzidos de uma vari´vel θ2 s˜o dados por
a
 j 
D2 w1
′ j j
 0  = (c2 − q ′ D2 )w2
′
c2 w2 − q ′ r1 r2
0
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

25. Problema de Precifica¸˜o - para P1 (P2 an´logo)
ca a
min (c1 − q ′ D1 )x1
′
x1 ∈ P1
Se o problema acima for ilimitado (custo = −∞), o M´todo Simplex
e
nos fornece um raio extremo w1  k que satisfaz (c ′ − q ′ D )w k < 0.
1 2 1
k

D1 w1
Neste caso, inserirmos a coluna  0  no master restrito
0
k
(associada a vari´vel θ1 ) e reotimizamos usando o primal Simplex.
a
j
Se o problema possui ´timo finito, atingido por x1 , de forma que
o
j
(c1 − q ′ D1 )x1 ≥ r1 , a solu¸˜o do Programa Master Reduzido resolve o
ca
j
Programa Master. Caso (c1 − q ′ D1 )x1 < r1 , uma coluna com custo
k
 
D 1 x1
reduzido negativo foi encontrado. Introduzimos a coluna  1  e
0
reotimizamos.
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca

26. Inicializa¸˜o do Algoritmo
ca
Precisamos encontrar uma solu¸˜o b´sica inicial para o Programa
ca a
Master.
Para tanto, aplicamos o Simplex Fase I para cada um dos
subproblemas Pi , separadamente. Com o simplex Fase I, obtemos os
1 1
pontos extremos x1 e x2 de P1 e P2 .
Construimos o Master Auxiliar e resolvemos o Simplex Fase I para
obter solu¸˜o b´sica para o Master Original.
ca a
m0
min yt
t=1
 
 λj Di xij +
i θik Di wik  + y = b0
i =1,2 j∈Ji k∈Ki
λj = 1, i = 1, 2
i
j∈Ji
λj
i ≥ 0, θik ≥ 0, yt ≥ 0, ∀i , k, j, t
Alexandre Salles da Cunha Otimiza¸˜o de Grande Porte
ca