1) O documento apresenta uma revisão sobre funções exponenciais e logarítmicas e introduz o número e. 2) É feita uma revisão sobre potências com bases reais positivas e expoentes reais. Logaritmos são definidos como o expoente ao qual se eleva a base para obter o valor. 3) O número e é definido como o limite de uma sequência e demonstrado que é irracional.

1. Aula 9
Fun»~es exponenciais e logar¶
co ³tmicas.
Uma revis~o e o n¶mero e
a u
Nesta aula faremos uma pequena revis~o das fun»~es f(x) = ax e g(x) = loga x, sendo
a co
a uma constante real, a > 0 e a 61. Faremos ainda uma apresenta»~o do n¶mero e,
= ca u
uma constante importante da matem¶tica universit¶ria.
a a
9.1 Pequena revis~o de pot^ncias
a e
Sabemos que, sendo a um n¶mero real positivo,
u
p p m
a1=n = n
a e am=n = n
a
se m; n 2 Z, e n > 0. Assim de¯ne-se a pot^ncia de base a e expoente p, ap (l^-se a
e e
elevado a p"), para todo p 2 Q.
Se ® ¶ um n¶mero irracional, existe uma seqÄ^ncia de n¶meros racionais que tende
e u ue u
a ® (uma seqÄ^ncia de aproxima»~es de ® por n¶meros racionais), ou seja, existe uma
ue co u
seqÄ^ncia de n¶meros racionais
ue u
®1 ; ®2 ; ®3 ; : : : ; ®n ; : : :
tal que lim ®n = ®.
n!+1
p
p Por exemplo, se ® = 2 ¼ 1;414213562, existe uma seqÄ^ncia de aproxima»~es
ue co
de 2, cujos cinco primeiros termos s~o dados na primeira coluna da tabela abaixo:
a
80

2. Funcoes exponenciais e logar¶
»~ ~ ¶
³tmicas. Uma revisao e o numero e 81
2
®1 = 1;4 (®1 = 1;96) j®1 ¡ ®j ¼ 0;014213562 < 0;1
2
®2 = 1;41 (®2 = 1;9881) j®2 ¡ ®j ¼ 0;004213562 < 0;01
2
®3 = 1;414 (®3 = 1;999396) j®3 ¡ ®j ¼ 0;000213562 < 0;001
2
®4 = 1;4142 (®4 = 1;99996164) j®4 ¡ ®j ¼ 0;000013562 < 0;0001
2
®5 = 1;41421 (®5 = 1;99998992) j®5 ¡ ®j ¼ 0;000003562 < 0;00001
p p
Uma calculadora nos fornece uma aproxima»~o de 2 com 12 casas decimais: 2 ¼
ca p
1;414213562373. A seqÄ^ncia acima, de aproxima»~es sucessivas de p 2, ¶ tal que
p ue p co e
j®n ¡ 2j < 10¡n , e assim lim j®n ¡ 2j = 0, e ent~o lim ®n = 2 (a segunda
a
n!+1 n!+1
2
coluna da tabela acima sugere que lim ®n = 2).
n!+1
Sendo a 2 R, a > 0, e sendo ® um n¶mero irracional, e ®1 ; ®2 ; ®3 ; : : : uma
u
seqÄ^ncia de racionais com limite ®, a® ¶ de¯nido como o limite da seqÄ^ncia
ue e ue
a®1 ; a®2 ; a®3 ; a®4 ; : : :
p
2
Por exemplo, 2 ¶ o limite da seqÄ^ncia
e ue
21 ; 21;4 ; 21;41 ; 21;414 ; : : :
Uma calculadora nos fornece as aproxima»~es:
co
21 = 2
p
21;4 = 214=10 =
10
214 ¼ 2; 6390
p
21;41 = 2141=100
100
= 2141 ¼ 2; 6574
21;414 = 21414=1000 ¼ 2; 6647
21;4142 = 214142=10000 ¼ 2; 6651
No que diz respeito a pot^ncias de base real positiva e expoente real, temos as
e
seguintes boas propriedades, que aceitaremos sem demonstra»~o:
ca
Se a 2 R, a > 0, e x; y 2 R
ax ¢ ay = ax+y
(ax )y = axy
1 ax
a¡x = x ; ax¡y = y ; a0 = 1
a a
x x x
a ¢ b = (ab) ; se tamb¶m b > 0
e

3. Funcoes exponenciais e logar¶
»~ ~ ¶
³tmicas. Uma revisao e o numero e 82
9.2 A fun»~o exponencial
ca
Sendo a um n¶mero real, positivo, a 61, de¯ne-se a fun»~o exponencial de base a
u = ca
por
f (x) = ax ; para todo x 2 R
Tomamos a 61 pela simples raz~o de que 1x = 1 para todo x 2 R, o que torna
= a
ax constante no caso em que a = 1 (fun»~es constantes n~o s~o classi¯cadas como
co a a
fun»~es exponenciais). Al¶m disso, tomamos a > 0 porque, se a < 0, ax n~o se de¯ne
co e a
para uma in¯nidade de valores reaisp x. Por exemplo, se a = ¡4 ent~o, para cada
de a
n 2 N, n ¸ 1, a1=2n = (¡4)1=2n = 2n ¡4 n~o se de¯ne como n¶mero real.
a u
Assumiremos que, se a > 0 e a = 1, a fun»~o exponencial dada por f(x) = ax, ¶
6 ca e
³nua em R, isto ¶,
cont¶ e
lim ax = ax0 ; para todo x0 2 R
x!x0
Assumiremos tamb¶m que se a > 1, a fun»~o f (x) = ax ¶ crescente, com lim ax =
e ca e
x!+1
+1, e se 0 < a < 1 a fun»~o ¶ decrescente, com lim ax = 0+ (= 0).
ca e
x!+1
¡ 1 ¢x
Na ¯gura 9.1 temos esbo»os dos gr¶¯cos de f(x) = 2x e g(x) =
c a 2
.
(a) (b)
y y
4 4
2 2
1 1
1/2 1/2
-2 -1 0 1 2 x -2 -1 0 1 2 x
Figura 9.1. Gr¶¯cos de (a) y = 2x , (b) y = (1=2)x .
a
Temos agora as seguintes novidades na ¶lgebra de limites:
a
1 1
Se a > 1, a+1 = +1, a¡1 = = = 0+ (= 0)
a+1 +1
1 1
Se 0 < a < 1, a+1 = 0+ (= 0), a¡1 = +1 = + = +1
a 0
Por exemplo,
¡ 1 ¢x ¡ 1 ¢+1 ¡ 1 ¢x
lim 2x = 2+1 = +1, lim 2x = 2¡1 = 0, lim 2
= 2
= 0, lim 2
=
x!+1 x!¡1 x!+1 x!¡1

4. Funcoes exponenciais e logar¶
»~ ~ ¶
³tmicas. Uma revisao e o numero e 83
¡ 1 ¢¡1
2
= 2+1 = +1.
9.3 Logaritmos e fun»~es logar¶
co ³tmicas
Se a > 0, a = 1, e x > 0, o logaritmo de x na base a, denotado por loga x, ¶ o
6 e
expoente ao qual devemos elevar a para obtermos x, ou seja
loga x = y se e somente se ay = x
Assim sendo,
aloga x = x
Por exemplo,
log2 8 = 3, pois 23 = 8;
p
log9 27 = 3 , pois 93=2 =
2
93 = 33 = 27;
1
log2 = ¡2, pois 2¡2 = 1=4;
4
¡ ¢¡4
log1=2 16 = ¡4, pois 12
= 16;
log2 5 ¼ 2; 3219, pois 22;3219 ¼ 4; 9999.
log2 5 n~o ¶ um n¶mero racional, pois se log2 5 = m , com m e n inteiros positivos,
a e u n
ent~o 2m=n = 5. Da¶ 2m = (2m=n )n = 5n , o que ¶ imposs¶ pois 2m ¶ par e 5n ¶
a ³, e ³vel e e
¶
³mpar.
Listamos aqui, sem dedu»~o, algumas propriedades elementares dos logaritmos:
ca
Sendo x e y reais positivos, z real, e a > 0; a 61,
=
loga (xy) = loga x + loga y
x
loga = loga x ¡ loga y
y
loga xz = z ¢ loga x
loga x
loga x1=z = (se z 60)
=
z
logb x
loga x = ; (se b > 0; b 61)
= (mudan»a de base)
c
logb a
Assim, por exemplo, a passagem dos logaritmos decimais (base 10) para os logar-
itmos de base 2 ¶ dada por
e
log10 x log x
log2 x = =
log10 2 log 2
Sendo a fun»~o f (x) = ax cont¶
ca ³nua e crescente quando a > 0, e decrescente
quando 0 < a < 1, temos que loga x ¶ de¯nida para todo x > 0.
e

5. Funcoes exponenciais e logar¶
»~ ~ ¶
³tmicas. Uma revisao e o numero e 84
Por exemplo, f (x) = 2x ¶ crescente, 22 = 4 e 23 = 8. Pela continuidade de f, a
e
imagem do intervalo [2; 3], pela fun»~o f , ¶ o intervalo [4; 8]. Existe ent~o x0 2 [2; 3]
ca e a
x0
tal que 2 = 5. Assim, log2 5 = x0 . Portanto, realmente existe o n¶mero real log2 5.
u
Al¶m disso, se a > 0, loga ¶ crescente, e se 0 < a < 1, loga ¶ decrescente.
e e e
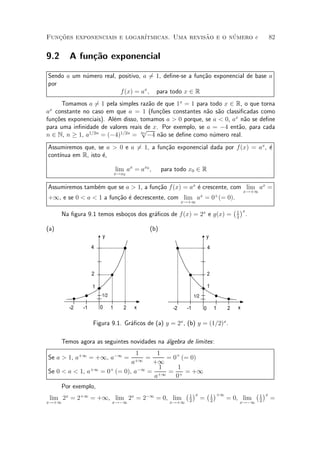
Na ¯gura 9.2, temos esbo»os dos gr¶¯cos de f(x) = log2 x e g(x) = log1=2 x.
c a
Admitiremos que f (x) = loga x ¶ cont¶
e ³nua no seu dom¶ ]0; +1[, ou seja,
³nio
se x0 > 0 ent~o lim loga x = loga x0
a
x!x0
Al¶m disso, temos ainda (con¯ra isto observando os gr¶¯cos da ¯gura 9.2).
e a
(
+ ¡1 se a > 0
lim loga x = loga (0 ) =
x!0+
+1 se 0 < a < 1
bem como tamb¶m (con¯ra observando os gr¶¯cos da ¯gura 9.2)
e a
(
+1 se a > 0
lim loga x = loga (+1) =
x!+1 ¡1 se 0 < a < 1
(a) (b)
y y
2 2
1 1
1/2 1 2 4
0 0
1 2 4 x 1/2 x
-1 -1
-2 -2
Figura 9.2. Gr¶¯cos de (a) y = log2 x, (b) y = log1=2 x.
a
9.4 O n¶mero e
u
Na matem¶tica universit¶ria, h¶ duas constantes num¶ricas muito importantes. S~o elas
a a a e a
o n¶mero pi, ¼ ¼ 3; 14159 , e o n¶mero e, e ¼ 2; 71828 .
u u

6. Funcoes exponenciais e logar¶
»~ ~ ¶
³tmicas. Uma revisao e o numero e 85
O n¶mero e ¶ de¯nido como sendo o limite
u e
µ ¶n
1
e = lim 1 +
n!+1
n2N
n
Pode ser demonstrado que o n¶mero e ¶ irracional.
u e
¡ ¢
1 n
Observe a tabela de valores (aproximados) de 1 + n , para n = 1, 10, 100,
1000, 10000, 100000, dada abaixo.
Tabela 9.1.
1
¡ ¢
1 n
n 1=n 1+ n
1+ n
1 1 2 21 = 2
10 0; 1 1; 1 (1; 1)10 ¼ 2; 59374
100 0; 01 1; 01 (1; 01)100 ¼ 2; 70481
1000 0; 001 1; 001 (1; 001)1000 ¼ 2; 71692
10000 0; 0001 1; 0001 (1; 0001)10000 ¼ 2; 71815
100000 0; 00001 1; 00001 (1; 00001)100000 ¼ 2; 71828
¡ 1
¢ 1
Note que lim 1+ n
=1+ +1
= 1.
n!+1
¡ ¢
1 n
Assim, podemos enganosamente intuir que, quando n ¶ muito grande, 1 + n ¼
e
1n = 1 (mesmo calculadoras de boa qualidade podem nos induzir a este erro). Neste
¡ ¢
1 n
caso, nossa intui»~o ¶ falha, pois pode ser demonstrado que o n¶mero an = 1 + n
ca e u
cresce µ medida em que n cresce, sendo a1 = 2, e 2 < an < 3 para cada n ¸ 2. Na
a
tabela 9.1, ilustramos o fato de que
µ ¶n
1
quando n ¶ muito grande, 1 +
e ¼ 2; 71828
n
³mbolo de indetermina»~o: 1§1 .
Assim sendo, temos um novo s¶ ca
Vamos admitir, sem demonstra»~o, que tamb¶m, para x real
ca e
¡ ¢
1 x
lim 1 + x = e
x!+1
Neste caso, podemos deduzir:
Proposi»~o 9.1
ca µ ¶x
1
lim 1 + =e
x!¡1 x

7. Funcoes exponenciais e logar¶
»~ ~ ¶
³tmicas. Uma revisao e o numero e 86
Demonstra»~o. De fato, fazendo a mudan»a de vari¶vel
ca c a
x = ¡(y + 1)
temos y = ¡x ¡ 1, e portanto x ! ¡1 se e somente se y ! +1.
Assim, sendo
µ ¶x µ ¶¡(y+1)
1 1
lim 1+ = lim 1 ¡
x!¡1 x y!+1 y+1
µ ¶¡(y+1)
y
= lim
y!+1 y + 1
µ ¶y+1
y+1
= lim
y!+1 y
µ ¶y+1
1
= lim 1 +
y!+1 y
µ ¶y µ ¶
1 1
= lim 1 + ¢ lim 1 +
y!+1 y y!+1 y
=e¢1=e
Como conseqÄ^ncia, temos tamb¶m
ue e
Proposi»~o 9.2
ca
1
lim (1 + x) x = e
x!0
Demonstra»~o. Mostraremos que
ca
1 1
lim (1 + x) x = e, e lim (1 + x) x = e.
+ ¡
x!0 x!0
Pondo ® = 1=x, temos que x ! 0+ se e somente se ® ! +1. Da¶
³
µ ¶®
1 1
lim (1 + x) x = lim 1 + =e
x!0+ ®!+1 ®
Al¶m disso, x ! 0¡ se e somente se ® ! ¡1. Da¶ pela proposi»~o 9.1,
e ³, ca
µ ¶®
1 1
lim (1 + x) x = lim 1 + =e
x!0¡ ®!¡1 ®
Se x > 0, chama-se logaritmo natural ou logaritmo neperiano de x ao logaritmo
ln x = loge x
Como e ¼ 2; 71828 > 1, a fun»~o f(x) = ln x ¶ crescente e seu gr¶¯co tem,
ca e a
qualitativamente, a forma do gr¶¯co de g(x) = log2 x, ¯gura 9.2 a.
a

8. Funcoes exponenciais e logar¶
»~ ~ ¶
³tmicas. Uma revisao e o numero e 87
A passagem dos logaritmos naturais para os logaritmos decimais (base 10) ¶ dada
e
por
loge x ln x
log10 x = =
loge 10 ln 10
9.5 Problemas
1. Calcule os seguintes limites. Lembre-se que 1§1 ¶ um s¶
e ³mbolo de indetermina»~o.
ca
¡ ¢
2 x
(a) lim 1 + x
x!+1
2 1
Sugest~o. Para contornar a indetermina»~o 1+1 , fa»a 1 +
a ca c x
=1+ y
¡ x ¢x
(b) lim 1+x
x!+1
x 1
Sugest~o. Para contornar a indetermina»~o 1+1 , fa»a
a ca c 1+x
= 1+ y
¡ 2x+3 ¢x+1 ¡ 3x+1 ¢x
(c) lim 2x+1 (d) lim 2x+3
x!¡1 x!+1
¡ 3x+1 ¢x ¡ ¢
1 2x
(e) lim 2x+3 (f) lim 1 ¡ 3x
x!¡1 x!¡1
p
Respostas. (a) e2
3
(b) 1=e (c) e (d) +1 (e) 0 (f) 1= e2
ah ¡1
2. Mostre que, sendo a > 0, lim = ln a.
h!0 h
Sugest~o: Trate o caso a = 1 em separado. Para a 61, fa»a a mudan»a de
a = c c
vari¶vel ah ¡ 1 = z, e ent~o h = ln(z + 1)= ln a.
a a
3. Usando o resultado do problema anterior, calcule
¡ ¢
(a) lim n ¢ a1=n ¡ 1 (sendo a > 0, a 61)
=
n!+1
eax ¡1
(b) lim x
x!0
eax ¡1 eax ¡1 eax ¡1
Sugest~o. lim
a x
= lim (a ¢ ax
) = a ¢ lim ax
x!0 x!0 x!0
eax ¡ebx
(c) lim x
x!0
eax ¡ebx (eax ¡1)¡(ebx ¡1)
Sugest~o. lim
a x
= lim x
x!0 x!0
eax ¡1
(d) lim bx
x!0 e ¡1
Respostas. (a) ln a (b) a (c) a ¡ b (d) a=b
1
4. Sendo f (x) = 2 x , calcule os limites laterais lim f(x) e lim f (x).
+ ¡
x!0 x!0
Resposta. +1 e 0, respectivamente.
1
5. Sendo g(x) = 1 , calcule os limites laterais lim g(x) e lim g(x).
1 + 2 x¡a x!a+ x!a¡
Resposta. 0 e 1, respectivamente.