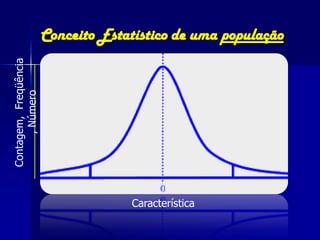
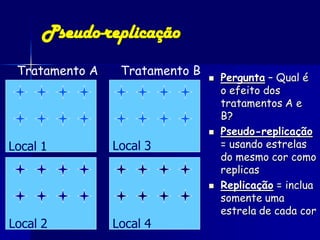
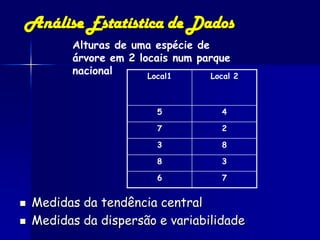
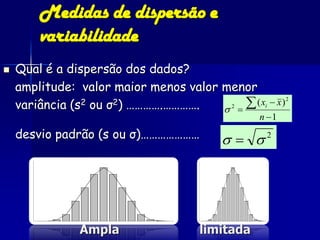
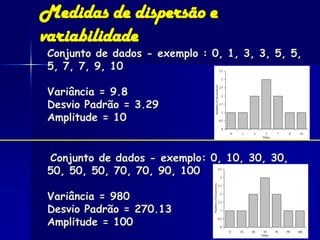
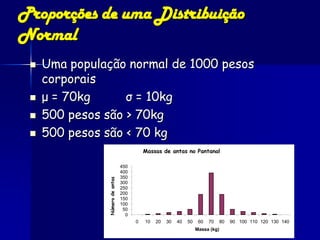
O documento fornece um resumo sobre análise estatística de dados ecológicos. Ele discute conceitos como amostragem, variáveis, populações, amostras, parâmetros e estatísticas. Além disso, explica medidas de tendência central, dispersão e variabilidade de dados, e testes estatísticos como t-teste, ANOVA e regressão que podem ser usados para analisar dados ecológicos.

1. Ecologia de Populações
Prof. Dr. Harold Gordon Fowler
19-3526-4230
popecologia@hotmail.com

2. Ecologia de Populações
Análise de Dados

3. Resumo
 Organizando um estudo ecológico
 Terminologia básica de amostragem
 Análise Estatística de Dados
– Por que usar estatística?
– Descrição de dados
 Medidas de tendência
 Medidas de dispersão
 Distribuição Normal
 Usando Excel
– Produzindo tabelas
– Produzindo gráficos
– Análise de dados
– Testes Estatísticos
 Teste-T
 ANOVA
 Regressão

4. Organizando um estudo ecológico
 Qual é o propósito da pesquisa?
 Qual é a pergunta principal levantada?
 Quais são suas hipóteses?
 Coleta de dados
 Resumo dos dados em tabelas
 Apresentação gráfica dos dados
 Teste estatístico das hipóteses
 Análise dos resultados estatísticos
 Apresentação de uma conclusão para a
pergunta inicial

5. Terminologia Básica de
Amostragem
 Elemento
 Variáveis
 Populações
 Amostras
 Parâmetros
 Estatísticas

6. Elemento
A unidade sobre qual coletamos
informação.
Tipicamente um indivíduo, mas pode
ser outro grupo social, planta, colonia
microbiana, etc.

7. O que é um variável?
 Variável: qualquer
característica definida que
varia entre entes biológicas
ou físicas.
 Exemplos: altura de plantas.
Peso de aves, cor do olho
humano, número de espécies
de árvores
 Se um indivíduo é selecionado
aleatoriamente de uma
população, pode demonstrar
um peso, altura ou outra
característica própria.
 Se vários indivíduos são
selecionados, suas
características podem ser
muito similares ou muito
diferentes.

8. População
É o grupo sobre qual queremos
tirar conclusões

9. O que é uma população?
 População: a coleção
inteira de medidas do
variável de interesse.
 Exemplo: se temos
interesse nas alturas de
árvores de uma espécie em
um parque nacional (Altura
da planta é nosso variável)
então nossa população
consiste de todas as
árvores da espécie no
parque nacional .

10. Conceito Estatístico de uma população
Contagem, Freqüência
, Número
Característica

11. Amostra
Um ou mais elementos
(indivíduos) da população

12. O que é uma amostra?
 Amostra: grupos menores
ou sub-conjuntos da
população que são usados
para estimar a distribuição
de um variável dentro da
população verdadeira
 Exemplo: as alturas de 100
árvores de uma espécie
num parque nacional podem
ser usadas para estimar as
alturas das árvores da
população intera (que pode
ser de milhares de
indivíduos)

13. Amostra com viés
Means that those selected are not
typical or representative of the
larger population from which they
have been selected

14. Parâmetro
É uma descrição resumida de um
variável na população

15. O que é um parâmetro?
 Parâmetro:
qualquer medida
calculada usada
para descrever ou
caracterizar uma
população
 Exemplo: a altura
média de árvores
de uma espécie
num parque
nacional

16. Propósitos da Replicação
 Controle de erro aleatório ou estocástico
– fatores independentes não testados podem
determinar o resultado do experimento
 Aumenta a precisão do teste
 Aumenta a capacidade geral do teste
– Se examine muitos locais – você pode
generalizar com segurança para outros locais

17. Algumas Definições
 Replica = Amostra
– Maximize essas no desenho experimental
– Maior número possível, sob as limitações
logísticas
– Se você é profissional, use a analise de poder
 Sub-amostra = Pseudo-replica
– Somente valida se as sub-amostras são
tratadas erradas como replicas verdadeiras
para a analise estatística
– Sub-amostras: úteis para aumentar a precisão
da estimativa dos dados da replica
– Um tipo especial de analise estatística pode
ser usado

18. Pseudo-replicação Definida
 “Replicação” errada
– Replicando amostras e não tratamentos
– Replicas não são independentes
 Problema é a violação das premissas
chaves da analise estatística:
– Independência das replicas
 Aumento da precisão dos estudos se são
independentes
 Aproxima a “verdade” melhor se
independente

19. Prevalência da Pseudo-
replicação
 48% de todos os estudos com pseudo-
replicação (Hurlbert 1984)
 71% dos estudos que usaram ANOVA (um
teste estatístico comum) com erros de
desenho (Underwood 1981)
 Mais marcado em estudos com problemas
de logística
– Animais raros
– Limitações de transporte ou financiamento
– Quase todo no Brasil!

20. Exemplos de Pseudo-replicas
 Muitas amostras de um local único
– Formam na verdade sub-amostras
 Somente uma amostra única para cada
tratamento
– Atualmente são replicas, mas não podemos fazer
estatística com um tamanho amostral de um
 Amostras solitárias de um local só, mas
replicadas no tempo
– Seriam amostras verdadeiras se a pergunta
experimental é dependente do tempo
– Se não, é uma pseudo-replicação

21. Pseudo-replicação
Tratamento A Tratamento B
 Pergunta – Qual é
o efeito dos
tratamentos A e
B?
 Pseudo-replicação
Local 1 Local 3 = usando estrelas
do mesmo cor como
replicas
 Replicação = inclua
somente uma
estrela de cada cor
Local 2 Local 4

22. Controle de Pseudo-replicação I
 Conheça sua pergunta
 Pergunta determina se o desenho
incluía a pseudo-replicação
 Nível Taxonômico
 Nível hierárquico ecológico
 Define claramente os variáveis
dependentes e independentes

23. Controle de Pseudo-replicação II
 O que conceitue uma unidade de dados?
– Ramo de arvore? Individuo? População? ....?
 Identifique qual é a unidade da replicação
– Individuo? População? Comunidade? Local?
– Replique de forma apropriada – locais
freqüentemente formam o nível de replicação
na ecologia
 Randomize seu desenho de amostragem
– Ajuda diminuir erros de amostragem

24. Na Disciplina
 Usaremos freqüentemente a pseudo-
replicação
– Limitações de tempo (pantanal!)
– Limitações de transporte (ônibus!)
– Limitações de esforço (você!)
 Por isso
– Lidaremos as pseudo-replicas como replicas
verdadeiras
 Mas – fique atente deste fato para após
criar projetos de pesquisa mais robustos
no futuro

25. O que é uma estatística?
 Estatística: uma
estimativa de qualquer
parâmetro populacional
 Exemplo: a altura média
de uma amostra de 100
árvores de uma espécie
num parque nacional

26. Por que usar estatísticas?
 Não é sempre possível obter medidas e calcular parâmetros
de variáveis na população de interesse
 A estatística permite estimar esses valores para a população
intera a base de variáveis aleatórios múltiplos do variável de
interesse
 Quanto maior o número de amostras, mais próxima fica a
medida estimada a medida verdadeira da população
 A estatística permite uma comparação eficiente de
populações para determinar as diferencias entre elas
 As estatística permite determinar relações entre os
variáveis

27. Análise Estatística de Dados
Alturas de uma espécie de
árvore em 2 locais num parque
nacional Local1 Local 2
5 4
7 2
3 8
8 3
6 7
 Medidas da tendência central
 Medidas da dispersão e variabilidade

28. Medidas da tendência central
 Onde fica o centro da distribuição?
media ( ou μ): media aritmética…… x
x
n
mediano: o valor na media de um conjunto ordenado de dados
modo: a valor que ocorre mais freqüentemente
Exemplo de conjunto de dados : 1, 2, 2, 2, 3, 5,
6, 7, 8, 9, 10
Media = (1 + 2 + 2 + 2+ 3 + 5 + 6 + 7 + 8 + 9 + 10)/11 = 55/11 = 5
Mediano = 1, 2, 2, 2, 3, 5, 6, 7, 8, 9,10 = 5
1, 2, 2, 2, 3, 5, 6, 7, 8, 9,10,11 = (5+6)/2 = 5.5
Modo = 1, 2, 2, 2, 3, 5, 6, 7, 8, 9, 10 = 2

29. Medidas de dispersão e
variabilidade
 Qual é a dispersão dos dados?
amplitude: valor maior menos valor menor
variância (s 2  
2 ou σ2) ………….…………. ( xi  x ) 2
n 1
desvio padrão (s ou σ)…………………   2
Ampla limitada

30. Medidas de dispersão e
variabilidade
Conjunto de dados - exemplo : 0, 1, 3, 3, 5, 5,
5, 7, 7, 9, 10 3.5
3
Variância = 9.8
Number of Occurences
2.5
2
Desvio Padrão = 3.29 1.5
Amplitude = 10
1
0.5
0
0 1 3 5 7 9 10
Value
Conjunto de dados - exemplo: 0, 10, 30, 30,
50, 50, 50, 70, 70, 90, 100 3.5
3
Number of Occurences
2.5
Variância = 980 2
Desvio Padrão = 270.13
1.5
1
Amplitude = 100
0.5
0
0 10 30 50 70 90 100
Value

31. Distribuição Normal dos Dados
 Um conjunto de dados no qual quase todos
os valores ficam próximos a média, e
existem poucas observações nos extremos
da amplitude dos dados
 Existe uma distribuição simétrica ao redor
da média

32. Proporções de uma Distribuição
Normal
 Uma população normal de 1000 pesos
corporais
 μ = 70kg σ = 10kg
 500 pesos são > 70kg
 500 pesos são < 70 kg
Massas de antas no Pantanal
450
400
350
Número de antas
300
250
200
150
100
50
0
0 10 20 30 40 50 60 70 80 90 100 110 120 130 140
Massa (kg)

33. Proporções de uma Distribuição
Normal Massas de antas no Pantanal
500
400
Número de antas
300
200
100
0
0 10 20 30 40 50 60 70 80 90 100 110 120 130 140
Quantos antas pesam > 80kg
Massa (kg)

 μ = 70kg σ = 10kg X = 80kg
 Usamos uma equação para nos informar quantos desvios
padrões doa meia está o valor de X :
Z=X–μ = Z = 80 – 70 =1
σ 10
 Depois usamos uma tabela para nos informar qual proporção
de uma população normal fica além desse valor de Z
 Essa proporção é igual a probabilidade de escolher
aleatoriamente um valor (X) maior do que 80kg

34. Tabela
de
valores
de Z
• Encontre o valor de Z na tabela (1.0)
• Encontre o valor de P associado (0.1587)
• O valor de P indica que existe uma probabilidade de 15.87%
((0.1587/1)x100) de que o urso escolhido de uma população de
1000 ursos medidos terá um peso maior do que 80kg

35. Distribuição de Probabilidade
 Existem várias tabelas de probabilidade
para tipos diferentes de testes
estatísticos.
exemplos. Tabela Z, Tabela t, Tabela de
Χ2
 Cada tabela permite a associação do
“valor crítico” com um valor de “P”
 Esse valor de P é usado para
determinar a significância do resultado
estatístico

36. Organizando um estudo ecológico
 Qual é o propósito da pesquisa?
 Qual é a pergunta principal levantada?
 Quais são suas hipóteses?
 Coleta de dados
 Resumo dos dados em tabelas
 Apresentação gráfica dos dados
 Teste estatístico das hipóteses
 Análise dos resultados estatísticos
 Apresentação de uma conclusão para a
pergunta inicial