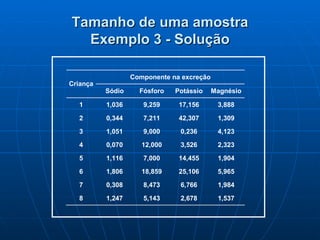
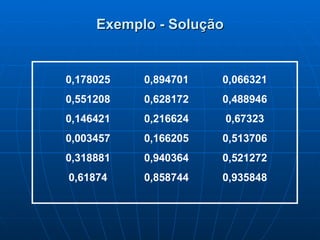
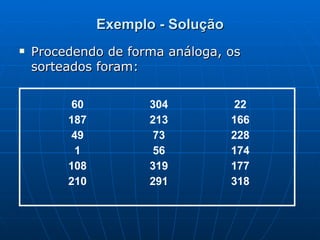
1) O documento discute os principais tipos de amostragem e como definir o tamanho adequado de uma amostra. 2) São descritos os tipos de amostragem aleatória simples, sistemática, por conglomerado e estratificada. 3) É explicado como gerar números aleatórios eletronicamente e como utilizá-los para selecionar uma amostra representativa de uma população.

1. Amostragem Prof. Gercino Monteiro Filho

2. Amostragem - Principio Por amostragem compreende como sendo as técnicas pelos quais possibilita a que uma amostra, quando coletada seja Não-tendenciosa.

3. Amostragem - Comentário Para cada área de atividade humana, a metodologia de coleta é diferente entre si, porem estas metodologias se baseiam nos mesmos princípios, princípios estes que serão vistos a seguir.

4. Tipos de Amostragem Amostra Aleatória Simples (AAS) Consiste em enumerar cada elemento de uma população e, a seguir, Sortear os Elementos da População que farão parte da amostra.

5. Tipos de Amostragem Amostragem Sistemática Cria-se uma LEI de formação para escolha dos elementos que irão compor a amostra. Ilustração: Policia Rodoviária: Parar para vistoriar todos os veículos com um dado final de placa, digamos 2.

6. Tipos de Amostragem Amostra Por Conglomerado Sorteia-se regiões da população e as sorteadas, todos os elementos dela farão parte da amostra. Ilustração Em uma pesquisa na cidade, sorteia quadras como um todo e entrevista cada um de seus moradores.

7. Tipos de Amostragem Amostragem Estratificada Divide a população em sub-populações que tenham o maior grau possível de homogeneidade e, dentro de cada uma destas sub-populações, toma-se uma amostra de forma proporcional ao tamanho de cada uma delas.

8. Tamanho de uma amostra Para a definição do tamanho da amostra necessária em uma pesquisa para representar a população, torna-se obrigatório: 1. Definição correta da População: Finita ou Infinita; 2. Ficar claro e conciso cada uma das variáveis conclusivas;

9. Tamanho de uma amostra Caracterizando as Variáveis 3 . Para cada uma das variáveis conclusivas, caracterizá-las por cada um dos tipos: Por Valor de Obtenção e Por Forma de Obtê-la, ainda assim é necessário deixar bem definido se a conclusão desejada é: Sobre o valor da variável; Sobre a porcentagem de incidência de cada um de seus valores.

10. Tamanho de uma amostra Caracterizando as Variáveis 4. Consultar, a priori, a existência de outros trabalhos sobre o assunto dos quais possa aproveitar informações que ajudarão na conclusão da pesquisa proposta, denominados Valores de Literatura, ou valores pressupostos inicialmente e que são conhecidos como Prevalência;

11. Tamanho de uma amostra Caracterizando as Variáveis 5. Escolher, a sua vontade, do Erro Máximo permitido de se cometer em seus parâmetros, erro este denominado: Erro Padrão de Estimativa, porém, obedecendo às condições de seu trabalho, a saber: Objetivo, Tempo e Dinheiro para a sua execução.

12. Tamanho de uma amostra Nota 1 No caso do desejado ser Valor, usa o modelo matemático da Média; no caso de Porcentagem, o modelo da proporção;

13. Tamanho de uma amostra Nota 2 Quando da Inexistência de Valores de Prevalência, ou de Literatura, para definir o Erro Padrão de Estimativa, recorre a: Se de Valor: Fazer uma Pré-Amostragem; Se de Porcentagem (Proporção), maximizar a amostra através do valor de p igual a 0,50.

14. Tamanho de uma amostra Fórmula baseado na Média População Infinita:

15. Tamanho de uma amostra Fórmula baseado na Média População Finita

16. Tamanho de uma amostra Fórmula baseado na Proporção População Infinita:

17. Tamanho de uma amostra Fórmula baseado na Proporção

18. Tamanho de uma amostra Fórmula baseado na Proporção Caso Especial: Devido a que, ao nível de 5,0%, o valor de Alfa ser: 1,96, aproxima de 2,00, e p desconhecido usa p=0,5 para maximizar a amostra, substituindo fica:

19. Tamanho de uma amostra Exemplo 1 Pesquisa : Avaliar a população de Goiânia quanto à prevenção em problemas cardíacos. Comentário sobre esta pesquisa. A pesquisa acima citada está sendo desenvolvida em Goiânia, em que teve inicio no ano de 2005, pelo Hospital das Clínicas da Universidade Federal de Goiás.

20. Tamanho de uma amostra Exemplo 1 Calcule o tamanho da amostra necessária para avaliar este perfil com erro padrão de estimativa de 2,0%, ao nível de significância de 0,05. Solução Analisando a pesquisa proposta O que se deseja é avaliar a população no tocante à quantia de adultos pelos quais faz prevenção com relação a saúde cardíaca e assim é de proporção (porcentagem).

21. Tamanho de uma amostra Solução do Exemplo 1 Desconhece a prevalência em Goiânia e assim maximiza pelo valor de p=0,500. Erro padrão de estimativa: e = 2,0% ou e = 0,02 Com α = 0,05, a distribuição normal fornece z 0 = 1,96. A população adulta de Goiânia é em torno de 600000 pessoas e assim trabalha como infinita.

22. Tamanho de uma amostra Solução do Exemplo 1 Como: Vem:

23. Tamanho de uma amostra Exemplo 2 Pesquisa: Fazer avaliação descritiva da população adulta goiana quanto à depressão Calcule o tamanho da amostra necessária para avaliar este perfil com erro padrão de estimativa de 2,5%, ao nível de significância de 0,05.

24. Tamanho de uma amostra Exemplo 2 - Solução Crítica da pesquisa: O que se deseja é avaliar a população no tocante à quantia de adultos pelos quais tem ou não a síndrome depressiva e assim é de proporção (porcentagem). Erro padrão de estimativa: e = 2,5%; Com α = 0,05, a distribuição normal fornece z 0 = 1,96.

25. Tamanho de uma amostra Exemplo 2 - Solução Desconhece a prevalência em Goiás (é o que deseja saber) ocorre que valor divulgado pela OMS em maio/2005 indicou que 20,0% da população mundial sofrem este sintoma, assim usa: p=0,200 como estimador inicial para achar o tamanho da população (p=0,20 é chamado Valor de Literatura).

26. Tamanho de uma amostra Exemplo 2 - Solução Como: Chega a:

27. Tamanho de uma amostra Exemplo 3 Pesquisa: Fazer análise sobre a fração de excreção urinária em crianças diabéticas. (Fração de excreção é a porcentagem de componentes na urina). Calcule o tamanho da amostra com erro de 10,0% da média ao nível de 5,0% de significância.

28. Tamanho de uma amostra Exemplo 3 - Solução Devido à inexistência de um valor de literatura disponível é necessário utilizar uma pré-amostragem, pelo qual em uma pesquisa realizada pelo HC/UFG pela acadêmica Cecília, obteve:

29. Tamanho de uma amostra Exemplo 3 - Solução

30. Tamanho de uma amostra Exemplo 3 - Solução Do sódio: Com o auxilio da informática obteve: Como o erro estipulado é 10,0% da média vem que:

31. Tamanho de uma amostra Exemplo 3 - Solução Com α = 0,05, a distribuição normal fornece z 0 = 1,96. O tamanho da amostra é:

32. Tamanho de uma amostra Exemplo 3 - Solução De fósforo Mesmo processo vem: Margem de erro:

33. Tamanho de uma amostra Exemplo 3 - Solução Na fórmula vem:

34. Tamanho de uma amostra Exemplo 3 - Solução De forma idêntica chega a:

35. Tamanho de uma amostra Exemplo 3 - Solução Como todas estas quatro variáveis são conclusivas, toma-se para amostra o maior valor encontrado, assim:

36. Uso de Números Aleatórios na Escolha da Amostra. Quando vai fazer uma amostragem, o sorteio pode ser feito de forma eletrônica, sendo que, para isso utiliza-se de uma função matemática descoberta pelo Matemático Randon e que tem todas as características de um sorteio feito mecanicamente.

37. Geração de Números Aleatórios de Forma Eletrônica. O número aleatório gerado de forma eletrônica está compreendido entre ZERO e UM, sendo gerado com 10 casas decimais ou mais;

38. Geração de Números Aleatórios de Forma Eletrônica. No caso do EXCEL, o procedimento é: Escolha a Célula onde deseja que o número fique escrito; Em fx, na Categoria da Função, escolha o modo MATEMÁTICO; No Nome da Função, selecione ALEATÓRIO; Clique e ele pede a SEMENTE, para isso basta clicar em OK, e o número será gerado na célula escolhida; Para gerar mais números aleatórios basta então ARRASTAR o cursor com o mouse na quantia desejada.

39. Números Aleatórios na Definição de Uma Amostra. Olhar inicialmente o Tamanho da População(N), ou seja o maior valor que possa ser contemplado; Definir o tamanho da amostra desejada (n); Na Planilha do Excel, gerar números aleatórios, no mínimo 50% acima do tamanho da amostra desejada (Devido a Repetições que ocorrerão); Copiar e COLAR ESPECIAL sob a forma de VALORES; Em outra coluna adjacente colocar a ordem de obtenção dos números aleatórios gerados;

40. Números Aleatórios na Definição de Uma Amostra. Em outra coluna multiplicar o Número Aleatório pelo valor do tamanho da população, acrescido de uma unidade (N + 1), formatando-os sob a forma de Número Inteiro (Nenhuma casa decimal); Copiar e COLAR ESPECIAL sob a forma de VALORES; Se o sorteio for COM REPOSIÇÃO, basta tomar os n primeiros e a amostra está OK;

41. Números Aleatórios na Definição de Uma Amostra. Se for SEM REPOSIÇÃO, eliminar as repetições, para facilidade de eliminação: Classificar os números aleatórios em ordem crescente, sendo que é OBRIGADO marcar o bloco também da coluna ORDEM para que permaneça na mesma seqüência gerada; Correr as células em sentido Vertical eliminando as repetições no EDITAR e EXCLUIR, eliminando as linhas repetidas; Classificar as duas colunas pela COLUNA Ordem; Tomar os n primeiros números da amostra gerada.

42. Números Aleatórios na Definição de Uma Amostra - Exemplo De uma Empresa que possui 340 funcionários será feita análise de Comportamento, sendo que para isto será utilizada uma amostra de 12 pessoas. Utilizando-se do Excel, encontre os componentes da amostra.

43. Exemplo - Solução Suponha inicialmente que os funcionários estejam identificados cada um por um número de 1 a 340. Utilizando-se da Planilha Excel, os números sorteados,lidos da esquerda para direita, foram:

44. Exemplo - Solução

45. Exemplo - Solução Multiplicam-se cada número da tabela por 341 (340+1),tomando a parte inteira, tal qual: 341 x 0,178025 = 60,706 e a parte inteira é 60; assim o primeiro sorteado é 60.

46. Exemplo - Solução Procedendo de forma análoga, os sorteados foram:

47. Exemplo - Solução Nesse exemplo não houve repetição de números, portanto os entrevistados serão, nessa ordem, os de números: 60 - 304 - 22 - 187 - 213 - 166 - 49 - 73 - 228 - 1 - 56 e 174

48. Amostragem Fim Prof. Gercino Monteiro Filho