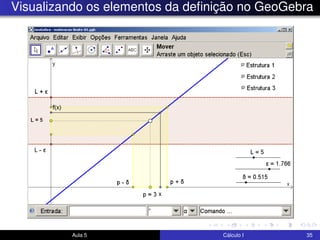
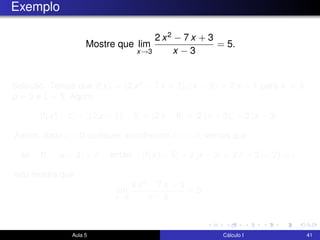
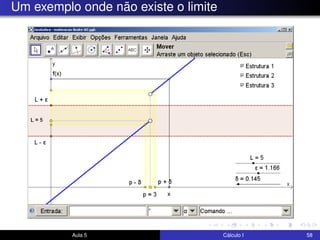
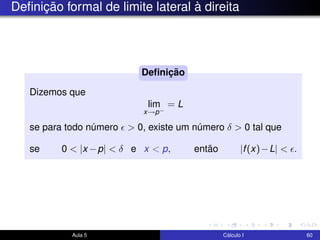
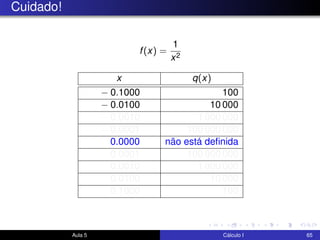
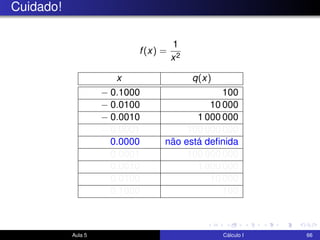
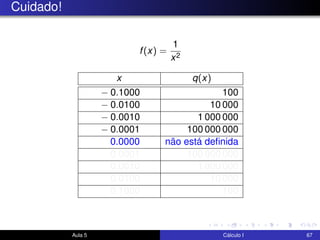
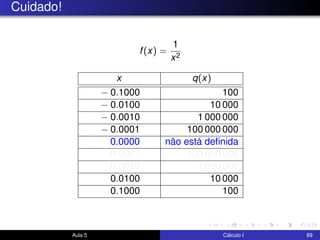
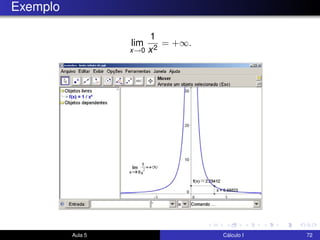
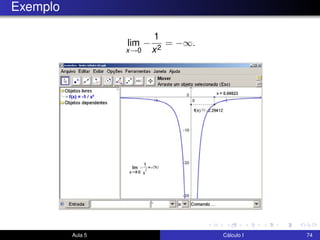
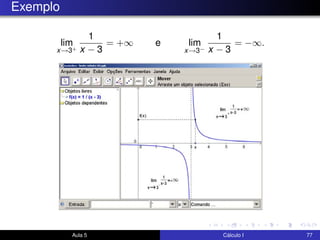
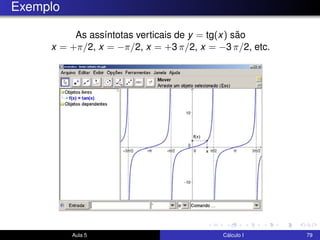
O documento descreve uma aula sobre cálculo I. Nela, o professor revisa teoremas como o teorema do confronto e do anulamento e resolve exercícios, incluindo o estudo do limite quando x tende a 0 de funções como x4cos(2x) e √x2sen(π/x). Ele também discute a motivação para a definição formal de limite e visualiza elementos da definição no GeoGebra.

1. Cálculo I
Humberto José Bortolossi
Departamento de Matemática Aplicada
Universidade Federal Fluminense
Aula 5
13 de setembro de 2007
Aula 5 Cálculo I 1

2. Exercícios da última aula
Aula 5 Cálculo I 2

3. Relembrando o teorema do confronto
Se f(x) ≤ g(x) ≤ h(x) quando x está próximo de p (exceto
possivelmente em p) e
lim
x→p
f(x) = L = lim
x→p
h(x),
então
lim
x→p
g(x) = L.
Teorema
Este teorema também é conhecido como
o teorema do sanduíche.
Aula 5 Cálculo I 3

4. Relembrando o teorema do anulamento
Se y = f(x) é uma função limitada em torno de um ponto p e
limx→p g(x) = 0, então
lim
x→p
(f(x) · g(x)) = 0.
Teorema
Aula 5 Cálculo I 4

5. Exercício [35] da página 110 do livro do Stewart
Estude lim
x→0
x4
cos
2
x
.
Solução. Temos que para todo x = 0, −1 ≤ cos(2/x) ≤ +1. Logo, multipli-
cando estas desigualdades por x4 para x = 0, vemos que
−x4
≤ x4
cos
2
x
≤ +x4
.
Como limx→0(−x)4 = 0 = limx→0(+x4), segue-se pelo teorema do confronto
que
lim
x→0
x4
cos
2
x
= 0.
Aula 5 Cálculo I 5

6. Exercício [35] da página 110 do livro do Stewart
Estude lim
x→0
x4
cos
2
x
.
Solução. Temos que para todo x = 0, −1 ≤ cos(2/x) ≤ +1. Logo, multipli-
cando estas desigualdades por x4 para x = 0, vemos que
−x4
≤ x4
cos
2
x
≤ +x4
.
Como limx→0(−x)4 = 0 = limx→0(+x4), segue-se pelo teorema do confronto
que
lim
x→0
x4
cos
2
x
= 0.
Aula 5 Cálculo I 6

7. Exercício [35] da página 110 do livro do Stewart
Estude lim
x→0
x4
cos
2
x
.
Solução. Temos que para todo x = 0, −1 ≤ cos(2/x) ≤ +1. Logo, multipli-
cando estas desigualdades por x4 para x = 0, vemos que
−x4
≤ x4
cos
2
x
≤ +x4
.
Como limx→0(−x)4 = 0 = limx→0(+x4), segue-se pelo teorema do confronto
que
lim
x→0
x4
cos
2
x
= 0.
Aula 5 Cálculo I 7

8. Exercício [35] da página 110 do livro do Stewart
Estude lim
x→0
x4
cos
2
x
.
Solução. Temos que para todo x = 0, −1 ≤ cos(2/x) ≤ +1. Logo, multipli-
cando estas desigualdades por x4 para x = 0, vemos que
−x4
≤ x4
cos
2
x
≤ +x4
.
Como limx→0(−x)4 = 0 = limx→0(+x4), segue-se pelo teorema do confronto
que
lim
x→0
x4
cos
2
x
= 0.
Aula 5 Cálculo I 8

9. Exercício [35] da página 110 do livro do Stewart
Estude lim
x→0
x4
cos
2
x
.
Solução. Temos que para todo x = 0, −1 ≤ cos(2/x) ≤ +1. Logo, multipli-
cando estas desigualdades por x4 para x = 0, vemos que
−x4
≤ x4
cos
2
x
≤ +x4
.
Como limx→0(−x)4 = 0 = limx→0(+x4), segue-se pelo teorema do confronto
que
lim
x→0
x4
cos
2
x
= 0.
Aula 5 Cálculo I 9

10. Exercício [35] da página 110 do livro do Stewart
Estude lim
x→0
x4
cos
2
x
.
Solução. Temos que para todo x = 0, −1 ≤ cos(2/x) ≤ +1. Logo, multipli-
cando estas desigualdades por x4 para x = 0, vemos que
−x4
≤ x4
cos
2
x
≤ +x4
.
Como limx→0(−x)4 = 0 = limx→0(+x4), segue-se pelo teorema do confronto
que
lim
x→0
x4
cos
2
x
= 0.
Aula 5 Cálculo I 10

11. Exercício [36] da página 110 do livro do Stewart
Estude lim
x→0+
√
x 2sen(π/x)
.
Solução. Temos que para todo x = 0, −1 ≤ sen(π/x) ≤ +1. Logo, exponen-
ciando, vemos que
2−1
≤ 2sen(π/x)
≤ 2+1
.
Isto mostra que y = f(x) = 2sen(π/x) é uma função limitada. Agora, como
limx→0+
√
x = 0, segue-se pelo teorema do anulamento que
lim
x→0+
√
x 2sen(π/x)
= 0.
Aula 5 Cálculo I 11

12. Exercício [36] da página 110 do livro do Stewart
Estude lim
x→0+
√
x 2sen(π/x)
.
Solução. Temos que para todo x = 0, −1 ≤ sen(π/x) ≤ +1. Logo, exponen-
ciando, vemos que
2−1
≤ 2sen(π/x)
≤ 2+1
.
Isto mostra que y = f(x) = 2sen(π/x) é uma função limitada. Agora, como
limx→0+
√
x = 0, segue-se pelo teorema do anulamento que
lim
x→0+
√
x 2sen(π/x)
= 0.
Aula 5 Cálculo I 12

13. Exercício [36] da página 110 do livro do Stewart
Estude lim
x→0+
√
x 2sen(π/x)
.
Solução. Temos que para todo x = 0, −1 ≤ sen(π/x) ≤ +1. Logo, exponen-
ciando, vemos que
2−1
≤ 2sen(π/x)
≤ 2+1
.
Isto mostra que y = f(x) = 2sen(π/x) é uma função limitada. Agora, como
limx→0+
√
x = 0, segue-se pelo teorema do anulamento que
lim
x→0+
√
x 2sen(π/x)
= 0.
Aula 5 Cálculo I 13

14. Exercício [36] da página 110 do livro do Stewart
Estude lim
x→0+
√
x 2sen(π/x)
.
Solução. Temos que para todo x = 0, −1 ≤ sen(π/x) ≤ +1. Logo, exponen-
ciando, vemos que
2−1
≤ 2sen(π/x)
≤ 2+1
.
Isto mostra que y = f(x) = 2sen(π/x) é uma função limitada. Agora, como
limx→0+
√
x = 0, segue-se pelo teorema do anulamento que
lim
x→0+
√
x 2sen(π/x)
= 0.
Aula 5 Cálculo I 14

15. Exercício [36] da página 110 do livro do Stewart
Estude lim
x→0+
√
x 2sen(π/x)
.
Solução. Temos que para todo x = 0, −1 ≤ sen(π/x) ≤ +1. Logo, exponen-
ciando, vemos que
2−1
≤ 2sen(π/x)
≤ 2+1
.
Isto mostra que y = f(x) = 2sen(π/x) é uma função limitada. Agora, como
limx→0+
√
x = 0, segue-se pelo teorema do anulamento que
lim
x→0+
√
x 2sen(π/x)
= 0.
Aula 5 Cálculo I 15

16. Exercício [36] da página 110 do livro do Stewart
Estude lim
x→0+
√
x 2sen(π/x)
.
Solução. Temos que para todo x = 0, −1 ≤ sen(π/x) ≤ +1. Logo, exponen-
ciando, vemos que
2−1
≤ 2sen(π/x)
≤ 2+1
.
Isto mostra que y = f(x) = 2sen(π/x) é uma função limitada. Agora, como
limx→0+
√
x = 0, segue-se pelo teorema do anulamento que
lim
x→0+
√
x 2sen(π/x)
= 0.
Aula 5 Cálculo I 16

17. Problemas de organização e
erros freqüentes
Aula 5 Cálculo I 17

18. Problemas de organização e erros freqüentes
Aula 5 Cálculo I 18

19. Problemas de organização e erros freqüentes
Aula 5 Cálculo I 19

20. Problemas de organização e erros freqüentes
Aula 5 Cálculo I 20

21. Problemas de organização e erros freqüentes
Aula 5 Cálculo I 21

22. Problemas de organização e erros freqüentes
Aula 5 Cálculo I 22

23. Problemas de organização e erros freqüentes
Aula 5 Cálculo I 23

24. Problemas de organização e erros freqüentes
Aula 5 Cálculo I 24

25. Problemas de organização e erros freqüentes
Aula 5 Cálculo I 25

26. Problemas de organização e erros freqüentes
Aula 5 Cálculo I 26

27. Problemas de organização e erros freqüentes
Aula 5 Cálculo I 27

28. As definições formais de limite e
limites laterais
Aula 5 Cálculo I 28

29. Motivação para a definição formal de limite
lim
x→3
2 x2 − 7 x + 3
x − 3
(∗)
= lim
x→3
2 (x − 1/2)(x − 3)
x − 3
= lim
x→3
(2 x − 1)
= 2 (3) − 1 = 5.
f(x) =
2 x2 − 7 x + 3
x − 3
= 2 x − 1, para x = 3.
Aula 5 Cálculo I 29
(∗) pois 2 x2 − 7 x + 3 = 2 (x − 1/2)(x − 3).

30. Motivação para a definição formal de limite
lim
x→3
2 x2 − 7 x + 3
x − 3
(∗)
= lim
x→3
2 (x − 1/2)(x − 3)
x − 3
= lim
x→3
(2 x − 1)
= 2 (3) − 1 = 5.
f(x) =
2 x2 − 7 x + 3
x − 3
= 2 x − 1, para x = 3.
Aula 5 Cálculo I 30
(∗) pois 2 x2 − 7 x + 3 = 2 (x − 1/2)(x − 3).

31. Motivação para a definição formal de limite
lim
x→3
2 x2 − 7 x + 3
x − 3
(∗)
= lim
x→3
2 (x − 1/2)(x − 3)
x − 3
= lim
x→3
(2 x − 1)
= 2 (3) − 1 = 5.
f(x) =
2 x2 − 7 x + 3
x − 3
= 2 x − 1, para x = 3.
Aula 5 Cálculo I 31
(∗) pois 2 x2 − 7 x + 3 = 2 (x − 1/2)(x − 3).

32. Motivação para a definição formal de limite
lim
x→3
2 x2 − 7 x + 3
x − 3
(∗)
= lim
x→3
2 (x − 1/2)(x − 3)
x − 3
= lim
x→3
(2 x − 1)
= 2 (3) − 1 = 5.
f(x) =
2 x2 − 7 x + 3
x − 3
= 2 x − 1, para x = 3.
Aula 5 Cálculo I 32
(∗) pois 2 x2 − 7 x + 3 = 2 (x − 1/2)(x − 3).

33. Motivação para a definição formal de limite
lim
x→3
2 x2 − 7 x + 3
x − 3
(∗)
= lim
x→3
2 (x − 1/2)(x − 3)
x − 3
= lim
x→3
(2 x − 1)
= 2 (3) − 1 = 5.
f(x) =
2 x2 − 7 x + 3
x − 3
= 2 x − 1, para x = 3.
Aula 5 Cálculo I 33
(∗) pois 2 x2 − 7 x + 3 = 2 (x − 1/2)(x − 3).

34. Motivação para a definição formal de limite
lim
x→3
2 x2 − 7 x + 3
x − 3
(∗)
= lim
x→3
2 (x − 1/2)(x − 3)
x − 3
= lim
x→3
(2 x − 1)
= 2 (3) − 1 = 5.
f(x) =
2 x2 − 7 x + 3
x − 3
= 2 x − 1, para x = 3.
Aula 5 Cálculo I 34
(∗) pois 2 x2 − 7 x + 3 = 2 (x − 1/2)(x − 3).

35. Visualizando os elementos da definição no GeoGebra
Aula 5 Cálculo I 35

36. Definição formal de limite
Seja f uma função definida em um intervalo aberto que
contém o número p, exceto possivelmente o próprio número p.
Então dizemos que o limite de f(x) quando x tende a p é
o número real L se para todo número > 0, existe um
número δ > 0 tal que
se 0 < |x − p|
distância entre x e p
< δ, então |f(x) − L|
distância entre f(x) e L
< .
Neste caso escreveremos
lim
x→p
f(x) = L.
Definição
Aula 5 Cálculo I 36

37. Definição formal de limite
Seja f uma função definida em um intervalo aberto que
contém o número p, exceto possivelmente o próprio número p.
Então dizemos que o limite de f(x) quando x tende a p é
o número real L se para todo número > 0, existe um
número δ > 0 tal que
se 0 < |x − p|
distância entre x e p
< δ, então |f(x) − L|
distância entre f(x) e L
< .
Neste caso escreveremos
lim
x→p
f(x) = L.
Definição
Aula 5 Cálculo I 37

38. Definição formal de limite
Seja f uma função definida em um intervalo aberto que
contém o número p, exceto possivelmente o próprio número p.
Então dizemos que o limite de f(x) quando x tende a p é
o número real L se para todo número > 0, existe um
número δ > 0 tal que
se 0 < |x − p|
distância entre x e p
< δ, então |f(x) − L|
distância entre f(x) e L
< .
Neste caso escreveremos
lim
x→p
f(x) = L.
Definição
Aula 5 Cálculo I 38

39. Definição formal de limite
Seja f uma função definida em um intervalo aberto que
contém o número p, exceto possivelmente o próprio número p.
Então dizemos que o limite de f(x) quando x tende a p é
o número real L se para todo número > 0, existe um
número δ > 0 tal que
se 0 < |x − p|
distância entre x e p
< δ, então |f(x) − L|
distância entre f(x) e L
< .
Neste caso escreveremos
lim
x→p
f(x) = L.
Definição
Aula 5 Cálculo I 39

40. Definição formal de limite
Seja f uma função definida em um intervalo aberto que
contém o número p, exceto possivelmente o próprio número p.
Então dizemos que o limite de f(x) quando x tende a p é
o número real L se para todo número > 0, existe um
número δ > 0 tal que
se 0 < |x − p|
distância entre x e p
< δ, então |f(x) − L|
distância entre f(x) e L
< .
Neste caso escreveremos
lim
x→p
f(x) = L.
Definição
Aula 5 Cálculo I 40

41. Exemplo
Mostre que lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Solução. Temos que f(x) = (2 x2 − 7 x + 3)/(x − 3) = 2 x − 1 para x = 3,
p = 3 e L = 5. Agora
|f(x) − L| = |(2 x − 1) − 5| = |2 x − 6| = |2 (x − 3)| = 2 |x − 3|.
Assim, dado > 0 qualquer, escolhendo δ = /2, vemos que
se 0 < |x − 3| < δ então |f(x) − 5| = 2 |x − 3| < 2 δ = 2 ( /2) = .
Isto mostra que
lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Aula 5 Cálculo I 41

42. Exemplo
Mostre que lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Solução. Temos que f(x) = (2 x2 − 7 x + 3)/(x − 3) = 2 x − 1 para x = 3,
p = 3 e L = 5. Agora
|f(x) − L| = |(2 x − 1) − 5| = |2 x − 6| = |2 (x − 3)| = 2 |x − 3|.
Assim, dado > 0 qualquer, escolhendo δ = /2, vemos que
se 0 < |x − 3| < δ então |f(x) − 5| = 2 |x − 3| < 2 δ = 2 ( /2) = .
Isto mostra que
lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Aula 5 Cálculo I 42

43. Exemplo
Mostre que lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Solução. Temos que f(x) = (2 x2 − 7 x + 3)/(x − 3) = 2 x − 1 para x = 3,
p = 3 e L = 5. Agora
|f(x) − L| = |(2 x − 1) − 5| = |2 x − 6| = |2 (x − 3)| = 2 |x − 3|.
Assim, dado > 0 qualquer, escolhendo δ = /2, vemos que
se 0 < |x − 3| < δ então |f(x) − 5| = 2 |x − 3| < 2 δ = 2 ( /2) = .
Isto mostra que
lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Aula 5 Cálculo I 43

44. Exemplo
Mostre que lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Solução. Temos que f(x) = (2 x2 − 7 x + 3)/(x − 3) = 2 x − 1 para x = 3,
p = 3 e L = 5. Agora
|f(x) − L| = |(2 x − 1) − 5| = |2 x − 6| = |2 (x − 3)| = 2 |x − 3|.
Assim, dado > 0 qualquer, escolhendo δ = /2, vemos que
se 0 < |x − 3| < δ então |f(x) − 5| = 2 |x − 3| < 2 δ = 2 ( /2) = .
Isto mostra que
lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Aula 5 Cálculo I 44

45. Exemplo
Mostre que lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Solução. Temos que f(x) = (2 x2 − 7 x + 3)/(x − 3) = 2 x − 1 para x = 3,
p = 3 e L = 5. Agora
|f(x) − L| = |(2 x − 1) − 5| = |2 x − 6| = |2 (x − 3)| = 2 |x − 3|.
Assim, dado > 0 qualquer, escolhendo δ = /2, vemos que
se 0 < |x − 3| < δ então |f(x) − 5| = 2 |x − 3| < 2 δ = 2 ( /2) = .
Isto mostra que
lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Aula 5 Cálculo I 45

46. Exemplo
Mostre que lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Solução. Temos que f(x) = (2 x2 − 7 x + 3)/(x − 3) = 2 x − 1 para x = 3,
p = 3 e L = 5. Agora
|f(x) − L| = |(2 x − 1) − 5| = |2 x − 6| = |2 (x − 3)| = 2 |x − 3|.
Assim, dado > 0 qualquer, escolhendo δ = /2, vemos que
se 0 < |x − 3| < δ então |f(x) − 5| = 2 |x − 3| < 2 δ = 2 ( /2) = .
Isto mostra que
lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Aula 5 Cálculo I 46

47. Exemplo
Mostre que lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Solução. Temos que f(x) = (2 x2 − 7 x + 3)/(x − 3) = 2 x − 1 para x = 3,
p = 3 e L = 5. Agora
|f(x) − L| = |(2 x − 1) − 5| = |2 x − 6| = |2 (x − 3)| = 2 |x − 3|.
Assim, dado > 0 qualquer, escolhendo δ = /2, vemos que
se 0 < |x − 3| < δ então |f(x) − 5| = 2 |x − 3| < 2 δ = 2 ( /2) = .
Isto mostra que
lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Aula 5 Cálculo I 47

48. Exemplo
Mostre que lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Solução. Temos que f(x) = (2 x2 − 7 x + 3)/(x − 3) = 2 x − 1 para x = 3,
p = 3 e L = 5. Agora
|f(x) − L| = |(2 x − 1) − 5| = |2 x − 6| = |2 (x − 3)| = 2 |x − 3|.
Assim, dado > 0 qualquer, escolhendo δ = /2, vemos que
se 0 < |x − 3| < δ então |f(x) − 5| = 2 |x − 3| < 2 δ = 2 ( /2) = .
Isto mostra que
lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Aula 5 Cálculo I 48

49. Exemplo
Mostre que lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Solução. Temos que f(x) = (2 x2 − 7 x + 3)/(x − 3) = 2 x − 1 para x = 3,
p = 3 e L = 5. Agora
|f(x) − L| = |(2 x − 1) − 5| = |2 x − 6| = |2 (x − 3)| = 2 |x − 3|.
Assim, dado > 0 qualquer, escolhendo δ = /2, vemos que
se 0 < |x − 3| < δ então |f(x) − 5| = 2 |x − 3| < 2 δ = 2 ( /2) = .
Isto mostra que
lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Aula 5 Cálculo I 49

50. Exemplo
Mostre que lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Solução. Temos que f(x) = (2 x2 − 7 x + 3)/(x − 3) = 2 x − 1 para x = 3,
p = 3 e L = 5. Agora
|f(x) − L| = |(2 x − 1) − 5| = |2 x − 6| = |2 (x − 3)| = 2 |x − 3|.
Assim, dado > 0 qualquer, escolhendo δ = /2, vemos que
se 0 < |x − 3| < δ então |f(x) − 5| = 2 |x − 3| < 2 δ = 2 ( /2) = .
Isto mostra que
lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Aula 5 Cálculo I 50

51. Exemplo
Mostre que lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Solução. Temos que f(x) = (2 x2 − 7 x + 3)/(x − 3) = 2 x − 1 para x = 3,
p = 3 e L = 5. Agora
|f(x) − L| = |(2 x − 1) − 5| = |2 x − 6| = |2 (x − 3)| = 2 |x − 3|.
Assim, dado > 0 qualquer, escolhendo δ = /2, vemos que
se 0 < |x − 3| < δ então |f(x) − 5| = 2 |x − 3| < 2 δ = 2 ( /2) = .
Isto mostra que
lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Aula 5 Cálculo I 51

52. Exemplo
Mostre que lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Solução. Temos que f(x) = (2 x2 − 7 x + 3)/(x − 3) = 2 x − 1 para x = 3,
p = 3 e L = 5. Agora
|f(x) − L| = |(2 x − 1) − 5| = |2 x − 6| = |2 (x − 3)| = 2 |x − 3|.
Assim, dado > 0 qualquer, escolhendo δ = /2, vemos que
se 0 < |x − 3| < δ então |f(x) − 5| = 2 |x − 3| < 2 δ = 2 ( /2) = .
Isto mostra que
lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Aula 5 Cálculo I 52

53. Exemplo
Mostre que lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Solução. Temos que f(x) = (2 x2 − 7 x + 3)/(x − 3) = 2 x − 1 para x = 3,
p = 3 e L = 5. Agora
|f(x) − L| = |(2 x − 1) − 5| = |2 x − 6| = |2 (x − 3)| = 2 |x − 3|.
Assim, dado > 0 qualquer, escolhendo δ = /2, vemos que
se 0 < |x − 3| < δ então |f(x) − 5| = 2 |x − 3| < 2 δ = 2 ( /2) = .
Isto mostra que
lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Aula 5 Cálculo I 53

54. Exemplo
Mostre que lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Solução. Temos que f(x) = (2 x2 − 7 x + 3)/(x − 3) = 2 x − 1 para x = 3,
p = 3 e L = 5. Agora
|f(x) − L| = |(2 x − 1) − 5| = |2 x − 6| = |2 (x − 3)| = 2 |x − 3|.
Assim, dado > 0 qualquer, escolhendo δ = /2, vemos que
se 0 < |x − 3| < δ então |f(x) − 5| = 2 |x − 3| < 2 δ = 2 ( /2) = .
Isto mostra que
lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Aula 5 Cálculo I 54

55. Exemplo
Mostre que lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Solução. Temos que f(x) = (2 x2 − 7 x + 3)/(x − 3) = 2 x − 1 para x = 3,
p = 3 e L = 5. Agora
|f(x) − L| = |(2 x − 1) − 5| = |2 x − 6| = |2 (x − 3)| = 2 |x − 3|.
Assim, dado > 0 qualquer, escolhendo δ = /2, vemos que
se 0 < |x − 3| < δ então |f(x) − 5| = 2 |x − 3| < 2 δ = 2 ( /2) = .
Isto mostra que
lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Aula 5 Cálculo I 55

56. Exemplo
Mostre que lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Solução. Temos que f(x) = (2 x2 − 7 x + 3)/(x − 3) = 2 x − 1 para x = 3,
p = 3 e L = 5. Agora
|f(x) − L| = |(2 x − 1) − 5| = |2 x − 6| = |2 (x − 3)| = 2 |x − 3|.
Assim, dado > 0 qualquer, escolhendo δ = /2, vemos que
se 0 < |x − 3| < δ então |f(x) − 5| = 2 |x − 3| < 2 δ = 2 ( /2) = .
Isto mostra que
lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Aula 5 Cálculo I 56

57. Exemplo
Mostre que lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Solução. Temos que f(x) = (2 x2 − 7 x + 3)/(x − 3) = 2 x − 1 para x = 3,
p = 3 e L = 5. Agora
|f(x) − L| = |(2 x − 1) − 5| = |2 x − 6| = |2 (x − 3)| = 2 |x − 3|.
Assim, dado > 0 qualquer, escolhendo δ = /2, vemos que
se 0 < |x − 3| < δ então |f(x) − 5| = 2 |x − 3| < 2 δ = 2 ( /2) = .
Isto mostra que
lim
x→3
2 x2 − 7 x + 3
x − 3
= 5.
Aula 5 Cálculo I 57

58. Um exemplo onde não existe o limite
Aula 5 Cálculo I 58

59. Definição formal de limite lateral à esquerda
Dizemos que
lim
x→p+
= L
se para todo número > 0, existe um número δ > 0 tal que
se 0 < |x −p| < δ e x > p, então |f(x)−L| < .
Definição
Aula 5 Cálculo I 59

60. Definição formal de limite lateral à direita
Dizemos que
lim
x→p−
= L
se para todo número > 0, existe um número δ > 0 tal que
se 0 < |x −p| < δ e x < p, então |f(x)−L| < .
Definição
Aula 5 Cálculo I 60

61. Limites infinitos e assíntotas verticais
Aula 5 Cálculo I 61

62. Cuidado!
f(x) =
1
x2
x q(x)
− 0.1000 100
− 0.0100 10 000
− 0.0010 1 000 000
− 0.0001 100 000 000
+ 0.0000 não está definida
+ 0.0001 100 000 000
+ 0.0010 1 000 000
+ 0.0100 10 000
+ 0.1000 100
Aula 5 Cálculo I 62

63. Cuidado!
f(x) =
1
x2
x q(x)
− 0.1000 100
− 0.0100 10 000
− 0.0010 1 000 000
− 0.0001 100 000 000
+ 0.0000 não está definida
+ 0.0001 100 000 000
+ 0.0010 1 000 000
+ 0.0100 10 000
+ 0.1000 100
Aula 5 Cálculo I 63

64. Cuidado!
f(x) =
1
x2
x q(x)
− 0.1000 100
− 0.0100 10 000
− 0.0010 1 000 000
− 0.0001 100 000 000
+ 0.0000 não está definida
+ 0.0001 100 000 000
+ 0.0010 1 000 000
+ 0.0100 10 000
+ 0.1000 100
Aula 5 Cálculo I 64

65. Cuidado!
f(x) =
1
x2
x q(x)
− 0.1000 100
− 0.0100 10 000
− 0.0010 1 000 000
− 0.0001 100 000 000
+ 0.0000 não está definida
+ 0.0001 100 000 000
+ 0.0010 1 000 000
+ 0.0100 10 000
+ 0.1000 100
Aula 5 Cálculo I 65

66. Cuidado!
f(x) =
1
x2
x q(x)
− 0.1000 100
− 0.0100 10 000
− 0.0010 1 000 000
− 0.0001 100 000 000
+ 0.0000 não está definida
+ 0.0001 100 000 000
+ 0.0010 1 000 000
+ 0.0100 10 000
+ 0.1000 100
Aula 5 Cálculo I 66

67. Cuidado!
f(x) =
1
x2
x q(x)
− 0.1000 100
− 0.0100 10 000
− 0.0010 1 000 000
− 0.0001 100 000 000
+ 0.0000 não está definida
+ 0.0001 100 000 000
+ 0.0010 1 000 000
+ 0.0100 10 000
+ 0.1000 100
Aula 5 Cálculo I 67

68. Cuidado!
f(x) =
1
x2
x q(x)
− 0.1000 100
− 0.0100 10 000
− 0.0010 1 000 000
− 0.0001 100 000 000
+ 0.0000 não está definida
+ 0.0001 100 000 000
+ 0.0010 1 000 000
+ 0.0100 10 000
+ 0.1000 100
Aula 5 Cálculo I 68

69. Cuidado!
f(x) =
1
x2
x q(x)
− 0.1000 100
− 0.0100 10 000
− 0.0010 1 000 000
− 0.0001 100 000 000
+ 0.0000 não está definida
+ 0.0001 100 000 000
+ 0.0010 1 000 000
+ 0.0100 10 000
+ 0.1000 100
Aula 5 Cálculo I 69

70. Cuidado!
f(x) =
1
x2
x q(x)
− 0.1000 100
− 0.0100 10 000
− 0.0010 1 000 000
− 0.0001 100 000 000
+ 0.0000 não está definida
+ 0.0001 100 000 000
+ 0.0010 1 000 000
+ 0.0100 10 000
+ 0.1000 100
Aula 5 Cálculo I 70

71. Cuidado!
f(x) =
1
x2
x q(x)
− 0.1000 100
− 0.0100 10 000
− 0.0010 1 000 000
− 0.0001 100 000 000
+ 0.0000 não está definida
+ 0.0001 100 000 000
+ 0.0010 1 000 000
+ 0.0100 10 000
+ 0.1000 100
Aula 5 Cálculo I 71

72. Exemplo
lim
x→0
1
x2
= +∞.
Aula 5 Cálculo I 72

73. Limite infinito (de um ponto de vista informal)
Seja f uma função definida em ambos os lados de p, exceto
possivelmente em p. Dizemos que
lim
x→p
f(x) = +∞
se podemos fazer os valores de f(x) ficarem arbitrariamente
grandes (tão grandes quanto quisermos) por meio de uma
escolha adequada de x nas proximidades de p, mas não igual
a p.
Definição
Aula 5 Cálculo I 73

74. Exemplo
lim
x→0
−
1
x2
= −∞.
Aula 5 Cálculo I 74

75. Limite infinito (de um ponto de vista informal)
Seja f uma função definida em ambos os lados de p, exceto
possivelmente em p. Dizemos que
lim
x→p
f(x) = −∞
se podemos fazer os valores de f(x) ficarem arbitrariamente
grandes, porém negativos, escolhendo-se valores de x
próximos de p, porém diferentes do próprio p.
Definição
Aula 5 Cálculo I 75

76. Limites laterais infinitos
Definições análogas podem ser dadas no caso de limites laterais:
lim
x→p+
f(x) = +∞, lim
x→p+
f(x) = −∞,
lim
x→p−
f(x) = +∞, lim
x→p−
f(x) = −∞.
Aula 5 Cálculo I 76

77. Exemplo
lim
x→3+
1
x − 3
= +∞ e lim
x→3−
1
x − 3
= −∞.
Aula 5 Cálculo I 77

78. Assíntota vertical
A reta x = p é uma assíntota vertical do gráfico de y = f(x) se
pelo menos uma das seguintes condições estiver satisfeita:
lim
x→p+
f(x) = +∞, lim
x→p+
f(x) = −∞,
lim
x→p−
f(x) = +∞, lim
x→p−
f(x) = −∞.
Definição
Aula 5 Cálculo I 78

79. Exemplo
As assíntotas verticais de y = tg(x) são
x = +π/2, x = −π/2, x = +3 π/2, x = −3 π/2, etc.
Aula 5 Cálculo I 79

80. Exemplo
A assíntota vertical de y = ln(x) é a reta
x = 0 (o eixo y).
Aula 5 Cálculo I 80