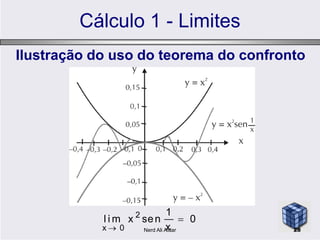
Propriedades dos Limites - Se L, M, a e c são números reais e n inteiro positivo, as seguintes propriedades são válidas: 1) Regra da soma e subtração: lim(f+g) = limf + limg e lim(f-g) = limf - limg 2) Regra do produto: lim(fg) = (limf)(limg) 3) Regra da divisão: lim(f/g) = (limf)/(limg) se lim g ≠ 0 4) Regra da potência: lim(f^

1. Ensino Superior
Cálculo 1
1.2- Propriedades dos Limites
Ali Aidar
1Nerd Ali Aidar

2. Sejam b e c dois números reais, e seja n um inteiro positivo.
Propriedades dos limites
x c
I) lim b b
II) lim x c



Obs.: Em IV, se n for par, c deve ser positivo.
x c
n n
x c
n n
x c
II) lim x c
III) lim x c
IV) lim x c






2Nerd Ali Aidar

3. Sejam b e c dois números reais, n um inteiro positivo e f e g
funções para as quais eLxf
cx


)(lim .)(lim Mxg
cx


Operação com limites


x c
I) lim [b.f(x )] bL         
f(x) L
IV) lim ; lim g(x) 0
g(x) M



  

x c
x c
x c
II) lim [f(x ) g(x )] L M
III) lim [f(x ).g(x )] L.M
Obs.: Em VI, se n for par, L deve ser positivo.
 
 


     


x c x c
n n
x c
nn
x c
IV) lim ; lim g(x) 0
g(x) M
V) lim f(x) L
VI) lim f(x) L
3Nerd Ali Aidar

4. Propriedades
 P1 - O limite da função identidade f(x) = x, quando x tende
a “a”, é igual a “a”.
ax lim
Operação com limites
3,0lim
3,0


x
x
3lim
3


x
x
ax
ax


lim
Exemplos:
3
5
5lim3


x
x




x
x
lim
ex
ex


lim
4Nerd Ali Aidar

5.  P2 - O limite de uma função constante f(x) = K, quando x
tende a “a”, é igual a própria constante:
KK
ax


lim
Operação com limites
KK
ax


lim
44lim
3

x
Exemplos:
33
55lim 
x
 
 2
lim
x
ee
x

 2
lim
5Nerd Ali Aidar

6.  P3 - O limite da soma é igual a soma dos limites
(caso esses limites existam):
  )(lim)(lim)()(lim xgxfxgxf
axaxax 

Operação com limites
1552.325limlim3lim
5lim3limlim)53(lim
2
22
2
2
22
2
2
2
2




xxx
xxxx
xx
xxxx
Exemplo:
6Nerd Ali Aidar

7.  P4 - O limite da diferença é igual a diferença dos limites
(caso esses limites existam):
  )(lim)(lim)()(lim xgxfxgxf
axaxax 

Operação com limites
  )(lim)(lim)()(lim xgxfxgxf
axaxax 

622.2limlim2
lim2lim)2(lim
2
2
2
2
2
2
2
2
2




xx
xxxx
xx
xxx
Exemplo:
7Nerd Ali Aidar

8.  P5 - O limite do produto é igual ao produto dos limites
(caso esses limites existam):
  )(lim).(lim)().(lim xgxfxgxf
axaxax 

Operação com limites
axaxax 
93.3lim.lim.lim)(lim
333
2
3


xxxxx
xxxx
Exemplo:
8Nerd Ali Aidar

9.  P6 - O limite do quociente é igual ao quociente dos limites
(caso esses limites existam):
)(lim
)(lim
)(
)(
lim
xg
xf
xg
xf ax







Operação com limites
)(lim)(
lim
xgxg
ax
ax






10
1
727
53
)7(lim
)5(lim
7
5
lim 3
3
3
33















 x
x
x
x
x
x
x
Exemplo:
9Nerd Ali Aidar

10.  P7 - O limite da potência de uma função (f(x))n, onde n é um
número inteiro positivo, é igual a potência do limite da
função (caso exista):
nn
xfxf ))(lim())((lim 
Operação com limites
n
ax
n
ax
xfxf ))(lim())((lim


813))2(lim()2(lim 443
1
43
1


xxxx
xx
Exemplo:
10Nerd Ali Aidar

11.  P8 - O limite da raiz de uma função , é a raiz do
limite da função, se o limite existe e é maior ou igual
a zero:
nn xfxf )(lim)(lim 
n xf )(
Operação com limites
n
ax
n
ax
xfxf )(lim)(lim


51)2(4)2()14(lim14lim 44
2
4
2


xxxx
xx
Exemplo:
11Nerd Ali Aidar

12. Cálculo 1 - Limites
Resumindo:
Propriedades dos Limites
 Se L, M, a e c são números reais e n inteiro
eLxf
ax


)(lim ,)(lim Mxg
ax


12Nerd Ali Aidar

13.  Regra da soma(subtração):
 Regra do Produto:
Regra da multiplicação por escalar:
MLxgxfxgxf
axaxax


)(lim)(lim)()(lim
MLxgxfxgxf
axaxax
.)(lim).(lim)().(lim 

Calculos Na Veia
 Regra da multiplicação por escalar:
 Regra do quociente:
Lcxfcxfc
axax
.)(lim.)(.lim 

M
L
xg
xf
xg
xf
ax
ax
ax



 )(lim
)(lim
)(
)(
lim
13Nerd Ali Aidar

14.  Regra da potência:
 Regra da raíz
nn
ax
n
ax
Lxfxf 

))(lim()(lim
Calculos Na Veia
 Regra da raíz
se é impar.
n
n
ax
n
ax
Lxfxf 

)(lim)(lim
nLxf
ax
,0)(lim 

14Nerd Ali Aidar

15.  Regra do logaritmo:
 Regra do seno (o mesmo para o cosseno)
0)(limlog
))(lim(log))((loglim




xfseL
xfxf
ax
c
ax
cc
ax
Calculos Na Veia
 Regra do seno (o mesmo para o cosseno)
 Regra da exponencial:
Lxfxf
axax
sen))(limsen()(senlim 

Lxfxf
ax
ccc ax
 

)(lim)(
lim
15Nerd Ali Aidar

16. Cálculo 1 - Limites
Se P(x) é uma função polinomial e c é um número real, então
)()(lim cPxP
cx


Limite de uma função polinomial
Teorema 2 – Os Limites de Funções Polinomiais podem ser
obtidos por Substituição:
Se 0
1
1 ...)( axaxaxP n
n
n
n  

então 0
1
1 ...)()(lim acacacPxP n
n
n
n
cx
 


16Nerd Ali Aidar

17. Cálculo 1 - Limites
Exemplo – Limite de Uma Função Polinomial
243lim 245
2x


xxxx
322246496
224164)32(3
2)2()2()2(4)2(3 245



17Nerd Ali Aidar

18. Cálculo 1 - Limites
Limites de Funções Racionais
Teorema 3 – Os Limites de Funções Racionais podem ser
obtidos por Substituição, caso o limite do
denominador não seja zero:denominador não seja zero:
Se e são polinômios e ,
então
)(xP )(xQ 0)( cQ
)(
)(
)(
)(
lim
cQ
cP
xQ
xP
cx


18Nerd Ali Aidar

19. Cálculo 1 - Limites
Exemplo – Limite de Uma Função Racional
0
03)1(4)1(34
lim
2323



 xx
0
65)1(5
lim 221



 xx
19Nerd Ali Aidar

20. Cálculo 1 - Limites
Exemplo 3 – Cancelando um Fator Comum
0
02
2
2
1
lim 


 xx
xx
x
Solução: Não podemos substituir x = 1 porque isso resulta em umSolução: Não podemos substituir x = 1 porque isso resulta em um
denominador zero. Testamos o numerador para ver se este também
é zero em x = 1. Também é, portanto apresenta o fator (x – 1) em
comum com o denominador. Cancelar o (x – 1) resulta em uma
fração mais simples, com os mesmos valores da original para x  1:
x
x
xx
xx
xx
xx 2
)1(
)2)(1(2
2
2







Se x  1
20Nerd Ali Aidar

21. Cálculo 1 - Limites
Usando a fração simplificada, obtemos o limite desses valores
quando x  1 por substituição:
)1(
)1)(2(2
limlim 2
2





xx
xx
xx
xx
)1(limlim 1
2
1 

  xxxx xx
3
1
212
lim1




 x
x
x
21Nerd Ali Aidar

22. Cálculo 1 - Limites



 )22(
22
lim hh
h
h
h
h
22
lim0


  
 22
22.22
lim 


hh
hh
Calcule

  )22(
lim0 hhh
22
1
202
1



 22
lim0 

 hhh
)22(
lim0 

 hh
h
h
22
1
lim0 

 hh
22Nerd Ali Aidar

23. Cálculo 1 - Limites
Vamos agora calcular alguns limites imediatos, de forma a facilitar o
entendimento dos exercícios mais complexos que virão em seguida:
a) lim (2x + 3) = 2.5 + 3 = 13
x 5
b) lim (x2 + x) = (+ ∞ )2 + (+ ∞ ) = + ∞ + ∞ = + ∞b) lim (x2 + x) = (+ ∞ )2 + (+ ∞ ) = + ∞ + ∞ = + ∞
x + ∞
c) lim (4 + x3) = 4 + 23 = 4 + 8 = 12
x 2
d) lim [(3x + 3) / (2x - 5)] = [(3.4 + 3) / (2.4 - 5)] = 5
x 4
e) lim [(x + 3) (x - 3)] = (4 + 3) (4 -3) = 7.1 = 7
x 4 23Nerd Ali Aidar

24. Cálculo 1 - Limites
R: -3
R: 0
3
21
3 2
1x
x x
Lim
x
 

g)
f)
1
452
1 

 x
xx
Lim
x
3
6
R:
4
31
1
1x
x
Lim
x


i)
3
1
1
1x
x
Lim
x


j) R: 2/3
0
3 3
x
x
Lim
x
 h)
R: 4/3
24Nerd Ali Aidar

25. Cálculo 1 - Limites
 Teorema do Confronto (ou Sanduíche)
Se
e f(x)  g(x)  h(x)
Lxhxf
axax


)(lim)(lim
então,
Exemplo:
Lxg
ax


)(lim


xxxfse
x
xf
x
3
20
)(,
)(
lim
25Nerd Ali Aidar

26. Cálculo 1 - Limites
Sabemos que:
Se |f(x)|  x3, então –x3  f(x)  x3
 Dividindo por x2 toda a inequação temos:
x
xf
x 
)(
 Pelo teorema do confronto:
x
x
xf
x
xxx 0200
lim
)(
lim)(lim


x
x
xf
x  2
)(
0
)(
lim0
)(
lim0 2020

 x
xf
x
xf
xx
26Nerd Ali Aidar

27. Cálculo 1 - Limites
Se f, g e h são funções que estão definidas em algum
intervalo aberto I que contém x0, exceto, possivelmente, no
  
Teorema do confronto
próprio x0, f(x)  g(x)  h(x), para todo x em I, tal que x  x0 e
então Lxhxf
xxxx


)(lim)(lim
00
Lxg
xx


)(lim
0
27Nerd Ali Aidar

28. Cálculo 1 - Limites
Ilustração do uso do teorema do confronto
2
x 0
1
l i m x sen 0
x

28Nerd Ali Aidar

29. Autor: Ali Aidar
Propriedades dos Limites
Nerd Ali Aidar 29