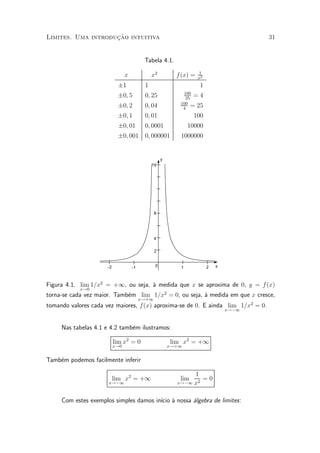
1) O documento introduz limites como ferramentas para estudar o comportamento de funções reais, fornecendo informações sobre suas propriedades gráficas. 2) A definição formal de limite é matematicamente sofisticada, mas uma exploração intuitiva do conceito através de exemplos é mais útil para calcular limites. 3) Limites podem ser finitos, infinitos ou indeterminados, e seu cálculo depende do comportamento da função quando o valor da variável se aproxima de um ponto.

1. Aula 4
Limites. Uma introdu»~o intuitiva
ca
Nos cap¶
³tulos anteriores, ¯zemos uso de um limite especial para calcular derivadas:
f (x) = lim f (x+¢x)¡f (x) .
0
¢x
¢x!0
Neste cap¶³tulo veremos os limites como ferramentas de estudo do comportamento
de fun»~es reais, provendo informa»~es importantes sobre seus gr¶¯cos.
co co a
A de¯ni»~o formal de limite ¶ matematicamente so¯sticada, requerendo muitas
ca e
horas de estudo para ser entendida. O leitor interessado poder¶ encontr¶-la em bons
a a
livros-textos de c¶lculo. Ocorre por¶m que a de¯ni»~o de limite tem pouca ou nenhu-
a e ca
ma serventia quando queremos calcular limites. Faremos uma explora»~o intuitiva do
ca
conceito de limite e de suas propriedades, atrav¶s de exemplos e interpreta»~es gr¶¯cas.
e co a
Exemplo 4.1 Considere a fun»~o f(x) = 2x + 3. Quando x assume uma in¯nidade de
ca
valores aproximando-se mais e mais de 0, o n¶mero 2x + 3 assume uma in¯nidade de
u
valores aproximando-se de 2 ¢ 0 + 3 = 3. Dizemos que o limite de f (x), quando x tende
a 0, ¶ igual a 3, e escrevemos
e
lim f (x) = 3
x!0
Suponhamos que f(x) ¶ uma fun»~o real de¯nida em uma reuni~o de intervalos, e
e ca a
que x0 ¶ um ponto no interior ou no extremo de um desses intervalos. Os matem¶ticos
e a
dizem que lim f (x) = L (L 2 R) quando podemos fazer f (x) arbitrariamente pr¶ximo
o
x!x0
de L, tomando x su¯cientemente pr¶ximo de x0 , mantendo x 6x0 . No exemplo acima,
o =
podemos fazer f (x) pr¶ximo de 3 o quanto quisermos, bastando tomar x bem pr¶ximo
o o
de 0.
Exemplo 4.2 Aqui temos uma lista de exemplos intuitivos.
28

2. »~
Limites. Uma introducao intuitiva 29
1. lim x = a (a 2 R)
x!a
2. lim xn = an (n 2 N, a 2 R)
x!a
3. Sendo p(x) = an xn + an¡1 xn¡1 + ¢ ¢ ¢ + a1 x + a0 , (an ; : : : ; a0 todos reais),
lim p(x) = an xn + an¡1 xn¡1 + ¢ ¢ ¢ + a1 x0 + a0 = p(x0 )
0 0
x!x0
x3 ¡ 3 lim (x3 ¡ 3) 8¡3
x!2
4. lim 2 = = =1
x!2 x + 1 lim (x 2 + 1) 4+1
x!2
De¯ni»~o 4.1 Nos exemplos acima, de limites com x tendendo a x0 , tivemos sempre
ca
x0 no dom¶
³nio de f e lim f(x) = f (x0 ). Quando isto ocorre, dizemos que f ¶ e
x!x0
³nua no ponto x0 .
cont¶
No pr¶ximo exemplo, temos um limite em que x ! x0 , mas x0 n~o est¶ no dom¶
o a a ³nio
de f .
x3 ¡ 8
Exemplo 4.3 Calcular lim .
x!2 x ¡ 2
3
Solu»~o. Note que, sendo f (x) = x ¡8 , temos que 2 6
ca x¡2
2 D(f). Quando x se aproxima
3
de 2, x se aproxima de 8. Um c¶lculo direto nos d¶ ent~o
a a a
x3 ¡ 8 0
lim =
x!2 x ¡ 2 0
Este resultado, 0=0, ¶ muito comum no c¶lculo de limites, e n~o tem signi¯cado como
e a a
valor de um limite. A express~o 0=0 ¶ um s¶
a e ³mbolo de indetermina»~o ocorrendo em uma
ca
tentativa de c¶lculo de um limite. A ocorr^ncia desta express~o signi¯ca que o limite
a e a
ainda n~o foi calculado.
a
³mbolo de indetermina»~o 0=0, neste exemplo fazemos
Para evitar o s¶ ca
x3 ¡ 8 (x ¡ 2)(x2 + 2x + 4)
lim = lim
x!2 x ¡ 2 x!2 x¡2
= lim (x2 + 2x + 4) (pois x ¡ 2 60)
=
x!2
2
= 2 + 2 ¢ 2 + 4 = 12
Exemplo 4.4 (C¶lculo de um limite com mudan»a de vari¶vel)
a c a
p
3
x+1¡1
lim =?
x!0 x

3. »~
Limites. Uma introducao intuitiva 30
Um c¶lculo direto nos d¶ 0=0, uma indetermina»~o.
a a ca
p
Fazendo y = 3 x + 1, temos y 3 = x + 1, e portanto x = y 3 ¡ 1.
Quando x tende a 0, y tende a 1 (em s¶³mbolos: se x ! 0, ent~o y ! 1). E a¶
a ³
temos
p
3
x+1¡1 y¡1
lim = lim 3
x!0 x y!1 y ¡ 1
y¡1
= lim
y!1 (y ¡ 1)(y 2 + y + 1)
1 1
= lim 2 =
y!1 y + y + 1 3
4.1 Limites in¯nitos. Limites no in¯nito
1
Consideremos agora a fun»~o f (x) =
ca . Temos que o dom¶ de f ¶ o conjunto dos
³nio e
x2
n¶meros reais diferentes de 0: D(f) = R ¡ f0g.
u
Observe a tabela 4.1. Ali ¯zemos uso do fato de que f ¶ uma fun»~o par : f (¡x) =
e ca
f (x) para todo x 2 D(f ).
Na primeira coluna da tabela 4.1, temos valores de x cada vez mais pr¶ximos de
o
0. Na ultima coluna, vemos que os valores correspondentes de f (x) tornam-se cada
¶
vez maiores. Neste exemplo, podemos fazer f (x) ultrapassar qualquer n¶mero positivo,
u
tomando x su¯cientemente pr¶ximo de 0. Dizemos que o limite de f (x), quando x
o
tende a 0 ¶ + in¯nito", e escrevemos
e
lim f (x) = +1
x!0
ou seja,
1
lim = +1
x!0 x2
A interpreta»~o geom¶trica de lim (1=x2 ) = +1 pode ser visualizada na ¯gura
ca e
x!0
4.1, onde temos um esbo»o do gr¶¯co da curva y = 1=x2 .
c a
Agora observe a tabela 4.2. Notamos agora que, µ medida que x cresce inde¯nida-
a
1
mente, assumindo valores positivos cada vez maiores, f (x) = 2 torna-se cada vez mais
x
pr¶ximo de 0. Isto tamb¶m ¶ sugerido pela ¯gura 4.1. Neste caso, dizemos que o limite
o e e
de f (x), quando x tende a + in¯nito", ¶ igual a 0, e escrevemos
e
1
lim =0
x!+1 x2

4. »~
Limites. Uma introducao intuitiva 31
Tabela 4.1.
1
x x2 f (x) = x2
§1 1 1
100
§0; 5 0; 25 25
=4
100
§0; 2 0; 04 4
= 25
§0; 1 0; 01 100
§0; 01 0; 0001 10000
§0; 001 0; 000001 1000000
y
16
8
4
2
-2 -1 0 1 2 x
Figura 4.1. lim 1=x2 = +1, ou seja, µ medida que x se aproxima de 0, y = f (x)
a
x!0
torna-se cada vez maior. Tamb¶m lim 1=x2 = 0, ou seja, µ medida em que x cresce,
e a
x!+1
tomando valores cada vez maiores, f(x) aproxima-se de 0. E ainda lim 1=x2 = 0.
x!¡1
Nas tabelas 4.1 e 4.2 tamb¶m ilustramos:
e
lim x2 = 0 lim x2 = +1
x!0 x!+1
Tamb¶m podemos facilmente inferir
e
1
lim x2 = +1 lim =0
x!¡1 x!¡1 x2
Com estes exemplos simples damos in¶ µ nossa ¶lgebra de limites:
³cio a a

5. »~
Limites. Uma introducao intuitiva 32
Tabela 4.2.
1
x x2 f (x) = x2
1 1 1
1
2 4 4
= 0; 25
1
5 25 25
= 0; 04
10 100 0; 01
100 10000 0; 0001
103 106 10¡6
(+1) + (+1) = +1 (¡1) + (¡1) = ¡1
(§1)2 = +1 (+1)(¡1) = ¡1
(+1)3 = +1 (¡1)3 = ¡1
(¡1)(inteiro positivo par) = +1 (¡1)(inteiro positivo ¶
³mpar)
= ¡1
1
=0
§1
+1 + c = +1 (c constante) ¡1 + c = ¡1 (c constante)
( (
+1 se c > 0 +1 se c < 0
c ¢ (+1) = c ¢ (¡1) =
¡1 se c < 0 ¡1 se c > 0
( (
+1 +1 se c > 0 ¡1 +1 se c < 0
= =
c ¡1 se c < 0 c ¡1 se c > 0
Mas aten»~o! Cautela com essa nova aritm¶tica"! Os resultados"
ca e
§1
§1
, (+1) ¡ (+1), (¡1) + (+1), 0 ¢ (§1)
s~o novos s¶
a ³mbolos de indetermina»~o. Nada signi¯cam como valores de limites. Se
ca
chegarmos a algum deles no c¶lculo de um limite, temos que repensar o procedimento
a
de c¶lculo.
a
3x2 ¡ 2x ¡ 1
Exemplo 4.5 Calcular lim
x!+1 x3 + 4
Solu»~o. Uma substitui»~o direta nos d¶
ca ca a
3x2 ¡ 2x ¡ 1 +1 ¡ (+1) ¡ 1
lim =
x!+1 x3+4 +1 + 4

6. »~
Limites. Uma introducao intuitiva 33
Para evitarmos s¶
³mbolos de indetermina»~o, fazemos
ca
2 1
3x2 ¡ 2x ¡ 1 x2 (3 ¡ x ¡ x2 )
lim = lim 4
x!+1 x3 + 4 x!+1 x3 (1 + x3 )
2 1
3 ¡ x ¡ x2
= lim
x!+1 x(1 + 4 )
x3
2 1
3 ¡ +1 ¡ +1
= 4
+1(1 + +1 )
3¡0 3
= = =0
+1 ¢ (1 + 0) +1
p(x)
Nos limites da forma lim , em que p(x) e q(x) s~o polin^mios em x, prevalecem
a o
x!§1 q(x)
os termos de maior grau de ambos os polin^mios, ou seja, se
o
p(x) = an xn + an¡1 xn¡1 + ¢ ¢ ¢ + a1 x + a0 ;
q(x) = bm xm + bm¡1 xm¡1 + ¢ ¢ ¢ + b1 x + b0
p(x) an xn
ent~o lim
a = lim .
x!§1 q(x) x!§1 bm xm
Deixamos a dedu»~o disto para o leitor, como um exerc¶
ca ³cio.
Por exemplo, no exemplo que acabamos de estudar, bastar¶
³amos fazer
3x2 ¡ 2x ¡ 1 3x2 3 3
lim = lim = lim = =0
x!+1 x3+4 x!+1 x 3 x!+1 x +1
Mas aten»~o. Isto s¶ vale para limites de quocientes de polin^mios, em que
ca o o
x ! §1.
Exemplo 4.6 Calcular lim (x5 ¡ x3 )
x!¡1
Temos
lim (x5 ¡ x3 ) = (¡1)5 ¡ (¡1)3 = (¡1) ¡ (¡1) = (¡1) + (+1), portanto
x!¡1
chegamos a um s¶
³mbolo de indetermina»~o.
ca
Podemos no entanto fazer
1
lim (x5 ¡ x3 ) = lim x5 (1 ¡ x2
) = +1 ¢ (1 ¡ 0) = +1.
x!¡1 x!¡1
1
Exemplo 4.7 Calcular lim .
x!0 x

7. »~
Limites. Uma introducao intuitiva 34
1
Solu»~o. Aqui podemos ser induzidos a dizer, tal como no exemplo do limite lim
ca 2,
x!0 x
1
que lim x ¶ in¯nito. Ok, mas qual in¯nito"? +1 ou ¡1 ? A resposta ¶, neste caso,
e e
x!0
nenhum dos dois!
Se x se aproxima de 0 por valores positivos, ent~o 1=x tende a +1. Por¶m se x
a e
se aproxima de 0 assumindo somente valores negativos, ent~o 1=x tende a ¡1 (j1=xj
a
¯ca cada vez maior, por¶m 1=x mant¶m-se sempre < 0).
e e
1
Neste caso, dizemos que n~o existe o limite lim .
a
x!0 x
1
O comportamento da fun»~o f (x) = , nas proximidades de x = 0, ser¶ melhor
ca a
x
estudado na pr¶xima aula, quando introduziremos o conceito de limites laterais.
o
4.2 Ilustra»~es geom¶tricas da ocorr^ncia de alguns
co e e
limites
Na ¯gura 4.2 temos o esbo»o de um gr¶¯co de uma fun»~o de¯nida no conjunto
c a ca
R ¡ fx0 g, para a qual lim f (x) = a e lim f (x) = b = f (x1 ).
x!x0 x!x1
y
y = f(x)
a
b
0 x0 x1 x
Figura 4.2. x0 n~o est¶ no dom¶ de f, lim f (x) = a, e lim f (x) = b = f (x1 )
a a ³nio
x!x0 x!x1
Na ¯gura 4.3 temos o esbo»o de um gr¶¯co de uma fun»~o de¯nida em todo o
c a ca
conjunto R, para a qual lim f (x) = a e lim f(x) = b.
x!+1 x!¡1
Na ¯gura 4.4 temos o esboco de um gr¶¯co de uma fun»~o de¯nida em R ¡ fag,
a ca
para a qual lim f (x) = +1. Na ¯gura 4.5 temos o esboco de um gr¶¯co de uma
a
x!a
fun»~o de¯nida em R ¡ fag, para a qual lim f (x) = ¡1. Na ¯gura 4.6 ilustramos o
ca
x!a
esboco de um gr¶¯co de uma fun»~o de¯nida em R ¡ fag, para a qual lim f (x) = ¡1,
a ca
x!a
lim f (x) = b e lim f (x) = ¡1.
x!¡1 x!+1

8. »~
Limites. Uma introducao intuitiva 35
y
y = f(x)
a
b
0 x
Figura 4.3. lim f(x) = a, e lim f (x) = b
x!+1 x!¡1
y
y = f(x)
0 a x
Figura 4.4. lim f (x) = +1
x!a
y
a
0 x
y = f(x)
Figura 4.5. lim f (x) = ¡1
x!a

9. »~
Limites. Uma introducao intuitiva 36
y
a
0 x
y = f(x)
b
Figura 4.6. lim f(x) = ¡1, lim f (x) = b, e lim f(x) = ¡1
x!a x!¡1 x!+1
4.3 Problemas
1. Calcule os limites.
x2 ¡ 4 x2 ¡ x
(a) lim (b) lim 2
x!2 x ¡ 2 x!1 2x + 5x ¡ 7
k 2 ¡ 16 (x + h)3 ¡ x3
(c) lim p (d) lim
k!4 k¡2 h!0 h
h3 + 8 1
(e) lim (f) lim
h!¡2 h + 2 z!10 z ¡ 10
1
(g) lim (h) lim (x2 + 3)(x ¡ 4)
p
x!1 (x ¡ 1)4 x! 2
2x2 + 5x ¡ 3
(i) lim 15
p (j) lim
x! 2 x!1=2 6x2 ¡ 7x + 2
x3 + 8 6s ¡ 1
(k) lim 4 (l) lim
x!¡2 x ¡ 16 s!4 2s ¡ 9
µ 2 ¶ p
x 1 4 ¡ 16 + h
(m) lim ¡ (n) lim
x!1 x ¡ 1 x¡1 h!0 h
2 3
(4t + 5t ¡ 3) (2 + h)¡2 ¡ 2¡2
(o) lim (p) lim
t!¡1 (6t + 5)4 h!0 h
2. Demonstre que se
p(x) = an xn + an¡1 xn¡1 + ¢ ¢ ¢ + a1 x + a0 ; e
q(x) = bm xm + bm¡1 xm¡1 + ¢ ¢ ¢ + b1 x + b0 ;
sendo a0 ; : : : ; an ; b0 ; : : : ; bn n¶meros reais com an 60 e bm 60, ent~o
u = = a

10. »~
Limites. Uma introducao intuitiva 37
p(x) an xn
(a) lim = lim
x!§1 q(x) x!§1 bm xm
(b) lim p(x) = lim an xn
x!§1 x!§1
3. Calcule os limites.
p
2x + 3 3
x2 + 1
(a) lim p (b) lim
x!+1 x + 3 x x!+1 x + 1
2x2 ¡ x + 3 2x2 ¡ 3x ¡ 4
(c) lim (d) lim p
x!+1 x3 ¡ 8x ¡ 5 x!¡1 x2 + 1
(2x + 3)3 (2 ¡ 3x)2 p p
(e) lim (f) lim ( x + a ¡ x)
x!+1 x5 + 5 x!+1
p p
(g) lim ( x2 + ax ¡ x) (h) lim (x + 3
1 ¡ x3 )
x!+1 x!+1
p p
(i) lim ( 3 x + 8x3 ¡ 2x) (j) lim x( x2 + 1 ¡ x)
x!+1 x!+1
4. Considerando as duas primeiras colunas da tabela 4.1, de valores para a fun»~o
ca
g(x) = x2 , Jo~ozinho argumentou que, quanto mais pr¶ximo de 0 ¶ o valor de x,
a o e
mais pr¶ximo de ¡1 ¯ca g(x). Explique porqu^ Jo~ozinho est¶ certo. Isto quer
o e a a
dizer que lim g(x) = ¡1 ? Explique.
x!0
4.3.1 Respostas e sugest~es
o
p
1. (a) 4 (b) 1=9 (c) 32 (d) 3x2 (e) 12 (f) n~o existe (g) +1 (h) 5 2 ¡ 20 (i) 15
a
(j) ¡7 (k) ¡3=8 (l) ¡23 (m) 2 (n) ¡1=8 (o) ¡64 (p) ¡1=4
2. (a)
³ ´
p(x) an xn 1 + an¡1 + ¢ ¢ ¢ + an xn¡1 + an xn
an x
a1 a0
lim = lim ³ ´
x!§1 q(x) x!§1 m 1 + bm¡1 + ¢ ¢ ¢ + b1 b0
bm x bm x bm xm¡1
+ bm xm
an xn 1 + an¡1 + ¢ ¢ ¢ +
an x
a1
an xn¡1
a0
+ an xn
= lim ¢ lim
x!§1 bm xm x!§1 1 + bm¡1 + ¢ ¢ ¢ + b1 b0
+ bm xm
bm x bm xm¡1
an xn 1 + an¡1 + ¢ ¢ ¢ + §1 + §1
§1
a1 a0
= lim ¢ lim
x!§1 bm xm x!§1 1 + bm¡1 + ¢ ¢ ¢ + b1 + b0
§1 §1 §1
an xn 1 + 0 + ¢¢¢ + 0 an xn
= lim ¢ = lim
x!§1 bm xm 1 + 0 + ¢ ¢ ¢ + 0 x!§1 bm xm
3. (a) 2 (b) 0 (c) 0
(d) +1. ¡ ¢ ¡ ¢
3 4 3 4
2x2 ¡ 3x ¡ 4 x2 2 ¡ x ¡ x2 x2 2 ¡ x ¡ x2
Sugest~o: lim
a p = lim q ¡ ¢ = lim q .
x!¡1 x2 + 1 x!¡1 1
x2 1 + x2
x!¡1 1
jxj 1 + x2
Agora, como x ! ¡1, temos x < 0, e ent~o jxj = ¡x.
a

11. »~
Limites. Uma introducao intuitiva 38
(e) 72 p p p p
p p ( x + a ¡ x)( x + a + x)
(f) 0. Sugest~o: x + a ¡ x =
a p p .
x+a+ x
(g) a=2 (h) 0. Sugest~o: Para contornar a indetermina»~o +1 ¡ 1, fa»a
a
p p p ca c
p3 (x + 3 1 ¡ x3 )[x2 ¡ x ¢ 3 1 ¡ x3 + ( 3 1 ¡ x3 )2 ]
x + 1 ¡ x3 = p p , e use a identidade
x2 ¡ x ¢ 3 1 ¡ x3 + ( 3 1 ¡ x3 )2
(a + b)(a2 ¡ ab + b2 ) = a3 + b3 .
(i) 0. Sugest~o: Aproveite a id¶ia usada na solu»~o do problema anterior, agora fazendo
a e ca
uso da identidade (a ¡ b)(a2 + ab + b2 ) = a3 ¡ b3 .
(j) 1=2