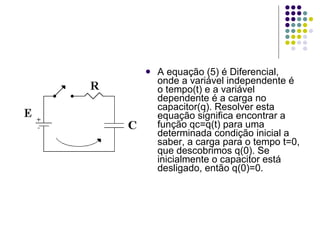
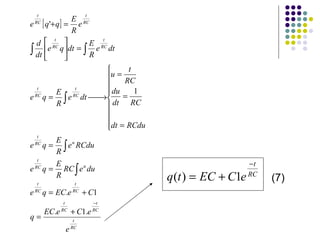
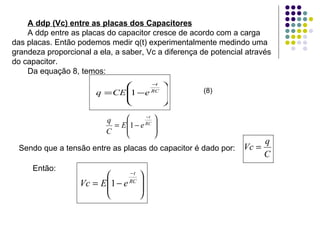
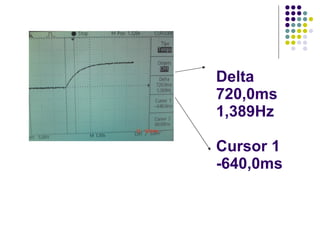
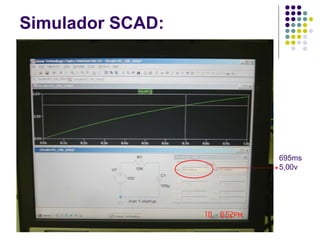
Este documento descreve um circuito RC e as equações que regem seu comportamento. A equação diferencial central é q(t)=q0e^(-t/RC), onde RC é chamado de constante de tempo do circuito e representa o tempo para a carga atingir aproximadamente 63% do seu valor final. O documento também explica como medir experimentalmente a carga no capacitor q(t) e a corrente i(t) no circuito para validar as equações teóricas.

1. UNOPAR – UNIVERSIDADE NORTE DO PARANÁ

4. Equações:

7. (7)

8. CONDIÇÃO Para uma condição inicial temos que, a carga para o tempo t=0, que denotamos q(0). Se inicialmente o capacitor está descarregado, então q(o)=0 Substituindo: (8) => Equação Solução

9. Matematicamente, se colocarmos t=0, teremos: De fato, a equação 8 prova que no instante t=0, o capacitor está descarregado, ou seja, q(0)=0. Sendo que experimentalmente podemos realizar três medidas e comprová-las.

10. A corrente no circuito i(t) varia no tempo e assim ela pode ser definida da seguinte forma: (2), derivando q em (9) função de t.

11. Substituindo q(t) “eq. 8” e sua derivada, ou seja, i(t) “eq.9” na equação diferencial “eq. 5”, temos: Mostra que a equação diferencial se reduz a uma identidade . De acordo com a 1ª Lei de KIRCHHOFEF, Lei da Tensões, a soma algébrica das diferenças de potencial em uma malha fechada é igual a ZERO.

12. A ddp (Vc) entre as placas dos Capacitores A ddp entre as placas do capacitor cresce de acordo com a carga das placas. Então podemos medir q(t) experimentalmente medindo uma grandeza proporcional a ela, a saber, Vc a diferença de potencial através do capacitor. Da equação 8, temos: (8) Sendo que a tensão entre as placas do capacitor é dado por: Então:

13. Analogamente, podemos medir i(t), medindo VR, ou seja, a diferença de potencial sobre o resistor. Sendo que a tensão entre os terminais do resistor é dada por: VR=R.i, como a corrente está variando com o tempo i(t), podemos substituir a eq. 6: em VR=R.i Assim: A figura X mostra os gráficos de Vc e de VR. Note que em qualquer instante a soma de Vc e Vr é igual E, como exige a equação 5.

14. Constante de Tempo O produto RC que aparece nas equações 8 e 9 tem dimensão de tempo (porque o expoente nas equações devem ser adimensional). Sendo assim, RC é chamado de constante de tempo capacitiva do circuito. Assim temos: Mas: Então:

15. Seu símbolo é a letra grega tau ( ) e sua unidade de medida é o segundo. Então : Ela é igual ao tempo necessário para que a carga do capacitor atinja uma função ou aproximadamente 63% é de seu valor final (de equilíbrio). Podemos mostrar isto, substituindo T=RC na eq. 8. Como (CE) é a carga de equilíbrio do capacitor correspondente quanto na equação.

16. Delta 720,0ms 1,389Hz Cursor 1 -640,0ms

17. Na Prática: Capacitor: 100uF Resistor: 10k Tensão: 10v

18. Jogando Valores: Erro Obtido: 3,5%

19. Simulador SCAD: 695ms 5,00v