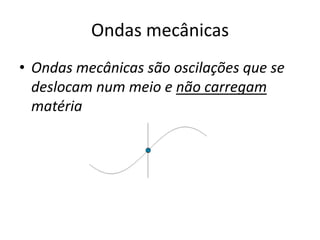
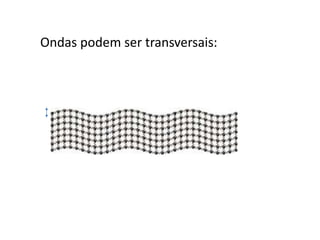
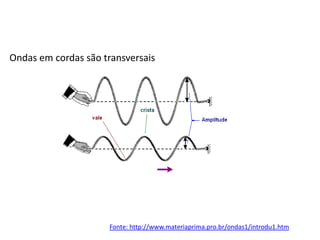
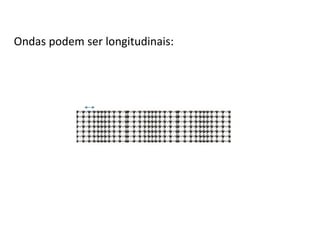
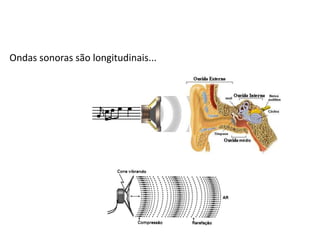
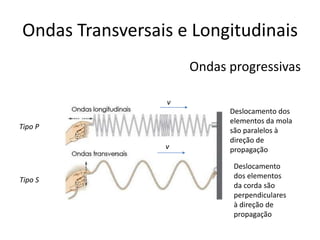
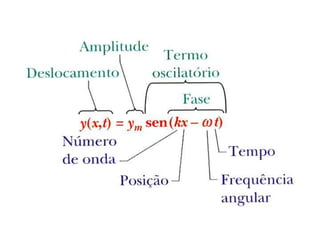
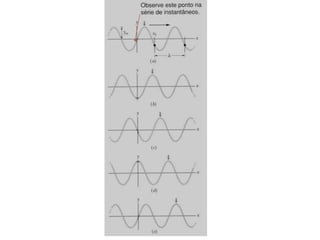
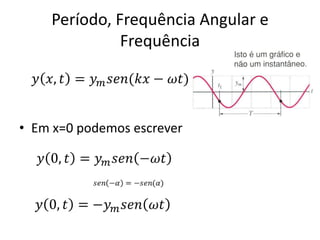
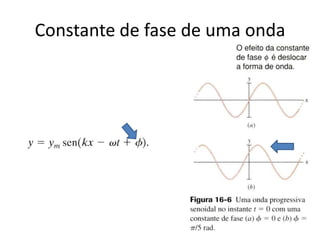
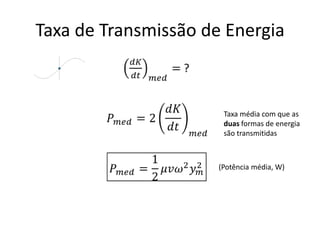
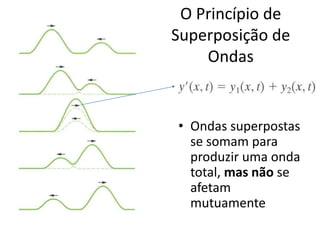
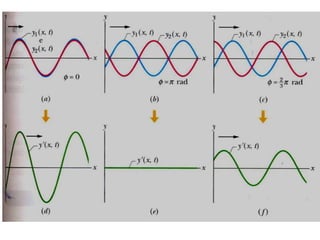
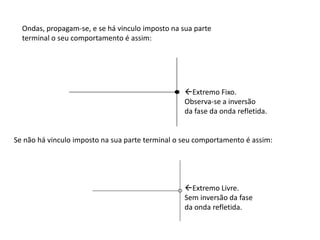
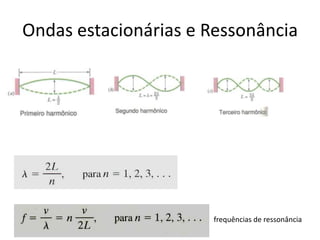
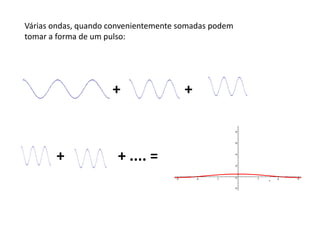
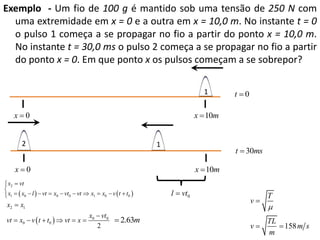
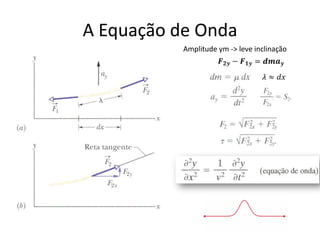
1) O documento apresenta um resumo sobre ondas mecânicas, abordando conceitos como comprimento de onda, frequência, velocidade e tipos de ondas (transversais e longitudinais). 2) É descrita a primeira usina de energia das ondas na América Latina, localizada no Ceará. 3) São explicados os três tipos de ondas: mecânicas, eletromagnéticas e ondas de matéria.

1. Física 2
Ondas I
Prof. Dr. Walmor Cardoso Godoi
Departamento de Física - DAFIS
Universidade Tecnológica Federal do Paraná – UTFPR
URL: http://www.walmorgodoi.com/utfpr
E-mail: walmorgodoi@utfpr.edu.br

2. Introdução
• Objetivo: Estudar propagação de ondas em:
– meios sólidos -> Ondas em cordas
– Meios fluidos -> Ondas sonoras

3. Introdução
A primeira usina de ondas da América Latina
funciona no porto do Pecém, a 60 quilômetros
de Fortaleza/CE.
• Brasil começa a explorar
energia limpa das ondas
• O litoral brasileiro, de
cerca de 8 mil quilômetros
de extensão, é capaz de
receber usinas de ondas
que produziriam 87 GW
(...) é possível converter
cerca de 20% disto em
energia elétrica, o que
equivaleria a 17% da
capacidade total instalada
no país.

4. As ondas podem ser divididas em 3
tipos:
• Ondas mecânicas
– Ondas do mar, ondas sonoras,
ondas sísmicas
– Leis de Newton
• Ondas eletromagnéticas
– Luz visível, raios X, ...
– Não precisam de meio material
para se propagar
– c = 299.792.458 m/s (vácuo)
• Ondas de matéria (ou onda de
Broglie)
– Dualidade onda-partícula
– Elétrons, prótons, átomos, e
outras partículas
Tipos de
Ondas

5. Ondas mecânicas
• Ondas mecânicas são oscilações que se
deslocam num meio e não carregam
matéria

6. Ondas podem ser transversais:

7. Ondas em cordas são transversais
Fonte: http://www.materiaprima.pro.br/ondas1/introdu1.htm

8. Ondas podem ser longitudinais:

9. Ondas sonoras são longitudinais...

10. Ondas Transversais e Longitudinais
Ondas progressivas
v
Tipo P
v
Tipo S
Deslocamento dos
elementos da mola
são paralelos à
direção de
propagação
Deslocamento
dos elementos
da corda são
perpendiculares
à direção de
propagação

11. Comprimento de Onda e Frequência
(01)
Para descrever uma
onda em uma corda
precisamos encontrar
uma função y(x,t)
(02)

14. Comprimento de Onda e Número de
Onda
• Em t=0
(03)
y é o mesmo nas duas extremidades do
comprimento de onda (em x=x1 e x=x1+λ)
Assim, de acordo com (03) teremos
(04)

15. Comprimento de Onda e Número de
Onda
• Função seno se repete em 2π rad, assim, na
equação anterior podemos fazer
(05)
(*número de onda, m-1)
*às vezes é denominado como o número
de onda angular ou número de onda
circular

16. Período, Frequência Angular e
Frequência
• Em x=0 podemos escrever

17. Período, Frequência Angular e
Frequência
• y é o mesmo nas duas extremidades do
período de oscilação (em t=t1 e t=t1+T)
Função seno se repete em 2π rad
(06)

18. Período, Frequência Angular e
Frequência
• A frequência será dada por

19. Resposta: a=2, b=3, c=1

20. Constante de fase de uma onda

21. Velocidade de uma onda
• Se o ponto A conserva seu
deslocamento, a fase deve-se
manter constante

22. Velocidade de uma onda
Fazendo
e

23. Exemplo 1
• Uma onda que se propaga em uma corda é
descrita por
y(x,t)=0,00327sen(72,1x-2,72t) (S.I.)
a)Amplitude
b)Comprimento de onda, T e f
c)Velocidade da onda
d)y para x=22,5 cm e t=18,9 s
a) 3,27 mm b) 0,0871 m, 2,31 s e 0,433Hz c) 3,77 cm/s d) y= 1,92 mm

24. Exemplo 2: Velocidade transversal
• Uma onda que se propaga em uma corda é
descrita por
y(x,t)=0,00327sen(72,1x-2,72t) (S.I.)
Se y=1,92 mm para x=22,5 cm e t=18,9 s
a) Velocidade transversal u?
c) Aceleração transversal ay?
a) 7,20 mm/s e b) -14,2 mm/s2

25. Velocidade da Onda em Uma Corda
Tracionada
• Velocidade da onda é determinada pelas
propriedades do meio.
• O meio deve possuir massa -> energia
cinética.
• O meio deve possuir elasticidade -> energia
potencial.

26. Velocidade da Onda em Uma Corda
Tracionada

27. Energia e Potência de uma Onda
Progressiva em Uma Corda
• Energia Cinética
Energia
potencial
nula e
cinética
máxima
Energia
potencial
máxima e
cinética
nula

28. Taxa de Transmissão de Energia
Taxa média com que as
duas formas de energia
são transmitidas
(Potência média, W)

29. • Exemplo 3. Uma corda tem massa específica
de 525 g/m e está submetida a uma tensão de
45 N. Uma onda senoidal de frequência f= 120
Hz e amplitude 8,5 mm é produzida na corda.
Com que taxa média a onda transporta
energia?
Resposta: 100 W

30. O Princípio de
Superposição de
Ondas
• Ondas superpostas
se somam para
produzir uma onda
total, mas não se
afetam
mutuamente

31. Interferência de Ondas
• Duas ondas que se propagam no mesmo sentido

33. • Exemplo 5. Duas ondas senoidais iguais,
propagando-se no mesmo sentido em uma
corda, interferem entre si. A amplitude das
ondas é 9,8 mm e a diferença de fase é 100
graus.
• A)Qual a amplitude da onda resultante?
• B) Que diferença de fase (em radianos e em
comprimentos de onda), faz com que a
amplitude de onda resultante seja 4,9 mm
• Resposta: a) 13 mm b) 2,6 rad e 0,42 comp.
onda

34. Fasores
• Pode-se representar uma onda numa corda
por um fasor
• Fasor -> vetor de módulo igual à amplitude
ym da onda que gira em torno da origem com
velocidade angular igual a frequência angular
da onda
• Pode-se usar fasores para combinar ondas
mesmo que as amplitudes sejam diferentes.

36. Fasores

37. • Exemplo: Duas ondas senoidais tem o mesmo
comprimento de onda e se propagam no
mesmo sentido de uma corda. As amplitudes
são ym1=4,0 mm e ym2=3,0 mm e as
constantes de fase são 0 e pi/3 rad. Quais são
a amplitude y´m e a constante de fase da onda
resultante?

38. Ondas Estacionárias

39. Ondas estacionárias
• Se duas ondas senoidais de mesma amplitude
e mesmo comprimento de onda se propagam
em sentidos opostos em uma corda, a
interferência mútua produz uma onda
estacionária.

40. Ondas estacionárias - nós
(nós)

41. Ondas estacionárias - antinós
(antinós)

42. Ondas, propagam-se, e se há vinculo imposto na sua parte
terminal o seu comportamento é assim:
Extremo Fixo.
Observa-se a inversão
da fase da onda refletida.
Se não há vinculo imposto na sua parte terminal o seu comportamento é assim:
Extremo Livre.
Sem inversão da fase
da onda refletida.

43. Ondas estacionárias e Ressonância

44. Ondas estacionárias e Ressonância
frequências de ressonância

45. Ondas estacionárias numa corda.
1/2 onda.

46. Ondas estacionárias numa corda.
Onda inteira.

47. Ondas estacionárias numa corda.
1½ de onda.

48. Várias ondas, quando convenientemente somadas podem
tomar a forma de um pulso:
+
+
+ .... =
+

49. • Exemplo 6. A Fig. 16.22 mostra a oscilação
ressonante de uma corda de massa m=2,5 x 10-3 kg e
comprimento L = 0,800 m sob uma tensão de 325,0
N. Qual é o comprimento de onda λ das ondas
transversais responsáveis pela onda estacionária e
qual o número harmônico n? Qual é a frequência f
das ondas transversais e das oscilações dos
elementos da corda? Qual é o módulo máximo da
velocidade transversal do elemento da corda que
oscila em x=0,180 m?

50. • Comprimento de onda e número harmônico
• Frequência
OU

51. • Velocidade transversal

52. Exemplo - Um fio de 100 g é mantido sob uma tensão de 250 N com
uma extremidade em x = 0 e a outra em x = 10,0 m. No instante t = 0
o pulso 1 começa a se propagar no fio a partir do ponto x = 10,0 m.
No instante t = 30,0 ms o pulso 2 começa a se propagar no fio a partir
do ponto x = 0. Em que ponto x os pulsos começam a se sobrepor?
1
x0
x  10m
2
1
t  30ms
x0
x  10m
 x2  vt


 x1   x0  l   vt  x0  vt0  vt  x1  x0  v  t  t0 

x2  x1
vt  x0  v  t  t0   vt  x 
t 0
x0  vt0
 2.63m
2
l  vt0
v
T
v
TL
 158 m s
m


53. A Equação de Onda
Amplitude ym -> leve inclinação