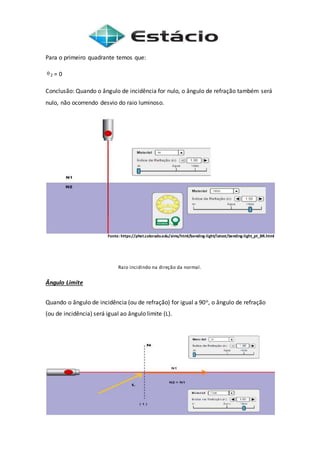
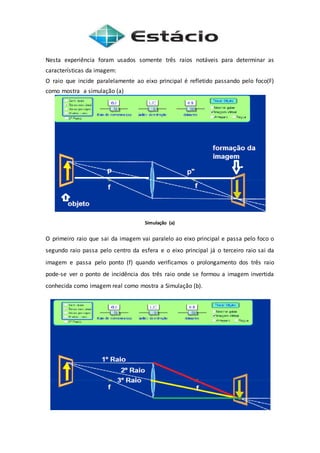
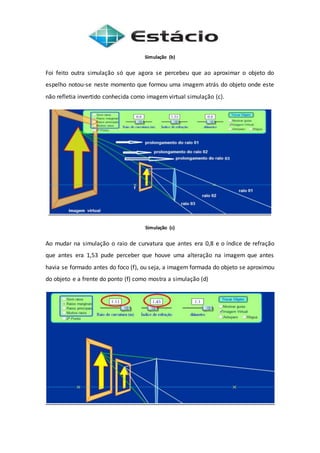
O documento descreve experimentos sobre a refração e reflexão da luz. Inclui a Lei de Snell que relaciona os ângulos de incidência e refração com os índices de refração dos meios. Também discute as características das imagens formadas por espelhos esféricos convexos e côncavos.

1. Universidade Estácio de Sá
CURSO DE ENGENHARIA ELÉTRICA
RELATÓRIO
Física Teórica Experimental II (CCE0847)
Experiência de da lei de Sneel
Professor: EricaCarvalho
ALUNOS: Ozinilda do Socorro Vieira Nacif RA: 201501247191
Data da pratica: 04/03/2016.
Data de entrega: 11/03/2016.
São Paulo
2016

2. Introdução
Demonstrar o comportamento da luz em um espelho plano e em lentes convergentes e
divergentes
Refração da Luz
Refração é a passagem da luz de um meio para outro.
Desde o século 19 já se sabia que a luz é uma forma de onda que se propaga com alta
velocidade, mas essa velocidade depende do meio por onde a luz está se propagando.
No ar, a velocidade da luz é quase 300.000 quilômetros por segundo. No interior de
um vidro transparente ela se reduz a uns "meros" 200.000 km/s. É essa mudança de
velocidade que faz o feixe de luz se desviar ao passar do ar para o vidro.
Observamos que, quando um raio de luz incidente for oblíquo, a refração é
acompanhada de desvio de direção, o que não acontece se a incidência do raio for
perpendicular.
Coloque um lápis, perpendicularmente, dentro de um copo de água. Você observará
olhando pela lateral do copo, que o lápis continuará na vertical dentro da água.
Colocando o lápis com uma inclinação dentro da água, você observará pela lateral do
copo que parece que o lápis está quebrado.
Lápis colocado inclinado na água
Fonte: https://pt.wikipedia.org/wiki/Reflex%C3%A3o_total

3. Um feixe de luz, incidindo obliquamente, muda de direção quando passa de um meio
transparente para outro transparente que apresenta velocidade da luz diferente do
primeiro meio.
Procedimento
Fonte: https://phet.colorado.edu/sims/html/bending-light/latest/bending-light_pt_BR.html
Quando a luz passa de um meio para outro, ocorre a refração além da reflexão.
O fenômeno da refração é regido pela Lei Snell-Descartes.
A lei da refração recebeu o nome dos dois cientistas, Snell e Descartes, porque apesar
de terem trabalhado independentemente, chegaram à mesma lei.·.
Lei Snell-Descartes
A lei de Snell - Relaciona os ângulos de incidência e refração com os índices de
refração.

4. A razão entre o seno do ângulo de incidência (θ1) e o seno do ângulo de refração (θ2)
é constante e esta constante é igual ao índice de refração relativo n21, para um dado
comprimento de onda.
sen 1 / sen 2 = n21 = n2 / n1 onde:
1 ângulo de incidência (ângulo que o raio incidente faz com a normal, N)
2 ângulo de refração (ângulo que o raio refratado faz com a normal, N)
n21 índice de refração relativo
n2 índice de refração do meio 2
n1 índice de refração do meio 1
Fonte: https://phet.colorado.edu/sims/html/bending-light/latest/bending-light_pt_BR.html

5. Refringência do meio
Quando o meio 2 for mais refringente que o meio 1, ou seja, quando o índice de
refração do meio 2, n2, for maior que o índice de refração do meio 1, n1, vamos ver o
que acontece com o raio refratado.
Pela Lei de Snell Descartes, temos que:
sen 1 / sen 2 = n2 / n1
Como n2 > n1 n2 / n1 > 1
Substituindo na Lei de Snell Descartes, obtemos:
sen 1 / sen 2 > 1 sen 1 > sen 2
Como 0 < 90o e a função seno é crescente no primeiro quadrante, temos:
1 > 2 ou 2 < 1
Conclusão: Quando o meio 2 for mais refringente que o meio 1 (n2 > n1), o raio
refratado se aproxima mais da normal no meio 2, ou seja, 2 < 1 .
O raio refratado se aproxima mais da normal no meio mais refringente.
Raio incidindo na direção normal
Quando o raio incidir na direção da normal, ou seja, o ângulo de 1 = 0º.
Pela Lei de Snell Descartes, obtemos:
sen 1 / sen 2 = n21
Sendo 1 = 0o sen 1 = 0
Substituindo na lei de Snell Descartes, obtemos:
0 = n21 sen 2
Como n21 é diferente de 0 sen 2 = 0

6. Para o primeiro quadrante temos que:
2 = 0
Conclusão: Quando o ângulo de incidência for nulo, o ângulo de refração também será
nulo, não ocorrendo desvio do raio luminoso.
Fonte: https://phet.colorado.edu/sims/html/bending-light/latest/bending-light_pt_BR.html
Raio incidindo na direção da normal.
Ângulo Limite
Quando o ângulo de incidência (ou de refração) for igual a 90o, o ângulo de refração
(ou de incidência) será igual ao ângulo limite (L).

7. Fonte: https://phet.colorado.edu/sims/html/bending-light/latest/bending-light_pt_BR.html
Fonte: https://phet.colorado.edu/sims/html/bending-light/latest/bending-light_pt_BR.html
1) O ângulo limite (L) sendo um ângulo de incidência
2) O ângulo limite (L) sendo um ângulo de refração.
Pela Lei de Snell Descartes, temos:
sen 1 / sen 2 = n21
1 = 90o sen 1 = 1 e 2 = L
Substituindo:
1 / sen L = n21
sen L = 1 / n21 = n12 = n1 / n2
Conclusão: O ângulo limite (L) é o maior ângulo (de incidência ou refração) para que
ocorra o fenômeno da refração e corresponde a um ângulo (de incidência ou de
refração) igual a 90º. (O ângulo limite (L) ocorre sempre no meio mais refringente).

8. Reflexão Total
Quando o ângulo de incidência ou de refração for maior que o ângulo limite (L), o raio
sofre uma reflexão total.
Reflexão total de um raio que incide com um ângulo maior que o ângulo limite (L).
Óticos Geométricos
Se tivermos a distância focal e posição do objeto é possível determinar,
analiticamente, a posição da imagem. Através da equação de Gauss, que é expressa
por:
O espelho esférico é constituído de uma superfície lisa e polido com formato esférico.
Se a parte refletora for interna será um espelho côncavo caso a superfície refletora
seja a parte externa será um espelho convexo.
Características das imagens nos espelhos esféricos

9. As características das imagens nos espelhos esféricos mudam de acordo com quando
mudamos a posição do objeto na frente do espelho.
Temos dois tipos de imagem, virtual e real:
Imagem virtual: é vista no ponto de encontro dos prolongamentos dos raios refletidos
Imagem real: é vista em um ponto onde realmente passam os raios refletidos
Podemos dizer como as imagens irão se comportar sabendo qual a posição do objeto
em relação ao espelho:
Espelhos Côncavos
Objeto localizado antes do centro de curvatura (C): A imagem é real, está posicionada
entre o centro de curvatura(C) e o foco(F), é invertida e o seu tamanho é menor que o
objeto.
Objeto localizado sobre o centro de curvatura (C): A imagem é real, está posicionada
sobre o centro de curvatura(C), é invertida e tem o mesmo do objeto.
Objeto localizado entre o centro de curvatura (C) e o foco (F): A imagem é real, está
posicionada antes do centro de curvatura(C), é invertida e o seu tamanho é maior que
o objeto.
Objeto localizado sobre o foco (F): A imagem é imprópria, pois os raios de luz saem
paralelos.
Objeto localizado entre o foco (F) e o vértice (V): A imagem é virtual, está posicionada
atrás do espelho ou depois do vértice(V), é direita e o seu tamanho é maior que o
objeto.
Os espelhos côncavos são muito usados por mulheres para passar maquiagem no
rosto, pois amplia a imagem.
Espelhos Convexos
A imagem nos espelhos convexos sempre será virtual, estará posicionada entre o
foco(F) e o vértice(V), será direita e o seu tamanho será menor que o objeto.
Os espelhos convexos são bastante utilizados nos retrovisores direito dos carros, pois
diminui a imagem para que caibam mais imagens no espelho, dando assim uma ampla
visão.

10. Nesta experiência foram usados somente três raios notáveis para determinar as
características da imagem:
O raio que incide paralelamente ao eixo principal é refletido passando pelo foco(F)
como mostra a simulação (a)
Simulação (a)
O primeiro raio que sai da imagem vai paralelo ao eixo principal e passa pelo foco o
segundo raio passa pelo centro da esfera e o eixo principal já o terceiro raio sai da
imagem e passa pelo ponto (f) quando verificamos o prolongamento dos três raio
pode-se ver o ponto de incidência dos três raio onde se formou a imagem invertida
conhecida como imagem real como mostra a Simulação (b).

11. Simulação (b)
Foi feito outra simulação só que agora se percebeu que ao aproximar o objeto do
espelho notou-se neste momento que formou uma imagem atrás do objeto onde este
não refletia invertido conhecida como imagem virtual simulação (c).
Simulação (c)
Ao mudar na simulação o raio de curvatura que antes era 0,8 e o índice de refração
que antes era 1,53 pude perceber que houve uma alteração na imagem que antes
havia se formado antes do foco (f), ou seja, a imagem formada do objeto se aproximou
do objeto e a frente do ponto (f) como mostra a simulação (d)

12. Simulação (d)
Conclusão
pode constatarna práticadas simulaçõesosdiversosfenômenosdaóticageométrica,inclusive
comparando elementos e informações da teoria com efeitos práticos observados nas
experiências. Concluímos que a luz ao passar de um meio a outro sofre diversas mudanças,
dentre elas a sua direção e o seu ângulo. Ao realizarmos um experimento percebemos que
após certoânguloo raio de luznão podiamaisservistoe a teorianos informa claramente que
esse fenômeno se dá devido ao ângulo de reflexão exceder o ângulo limite. Dentre esses e
outros fenômenos essa prática pode nos fornecer uma dimensão ampla das leis da ótica
geométrica.

13. Bibliografia
https://phet.colorado.edu/sims/html/bending-light/latest/bending-light_pt_BR.html
Acesso em: 04/02/2016.
https://phet.colorado.edu/sims/geometric-optics/geometric-optics_pt_BR.html.
Acessoem:04/03/2016.
https://pt.wikipedia.org/wiki/Reflex%C3%A3o_total
Acesso em: 05/06/2016.
http://www.infoescola.com/optica/espelhos-esfericos/.
Acessoem:05/06/2016.