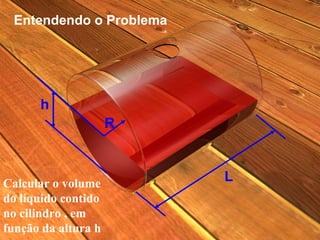
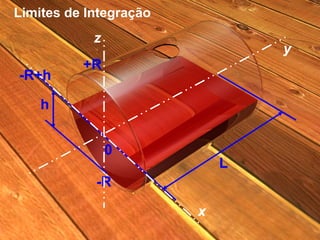
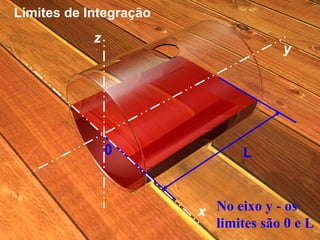
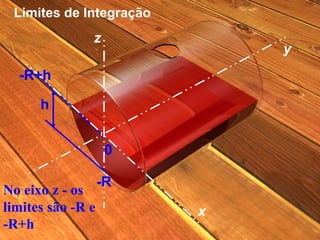
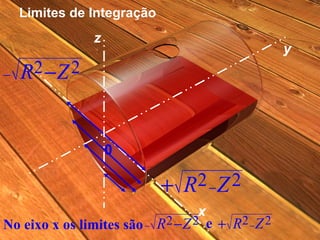
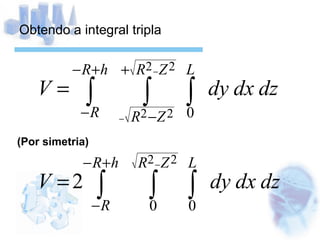
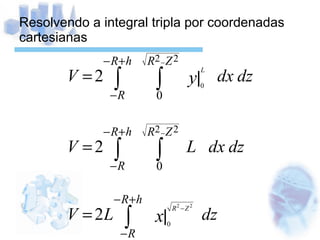
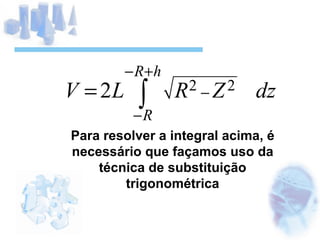
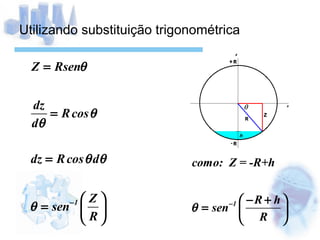
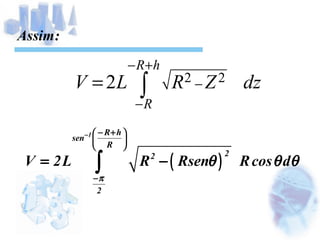
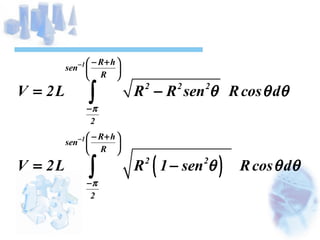
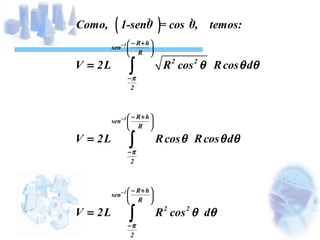
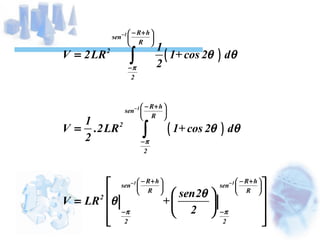
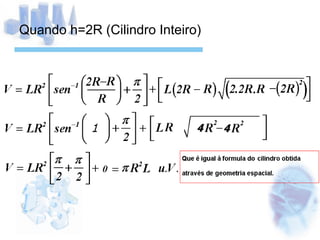
O documento descreve o cálculo do volume de um líquido dentro de um cilindro em função da altura do líquido. Os alunos calculam a integral tripla do volume e realizam medidas experimentais com diferentes volumes de líquido para validar a equação obtida. As medidas experimentais apresentaram pequenas diferenças em relação aos valores esperados, devido a possíveis erros de medição.

1. Cálculo do volume de líquido no interior de um cilindro deitado em função da altura (h) formada entre o fundo do cilindro e a superfície deste líquido

2. Alunos: Carlos Eduardo Gonçalves Arantes Cassiano Germanovix de Oliveira Eduardo Rovanni do Nascimento Rodrigo de Jesus Godoy Curso: Engenharia Elétrica Disciplina: Cálculo II Professor: Valdemir Antunes Turma: 3º Semestre

3. Entendendo o Problema Calcular o volume do líquido contido no cilindro , em função da altura h

4. Entendendo o Problema Calcular o volume do líquido contido no cilindro , em função da altura h L h R

5. Limites de Integração L h +R -R 0 y x z -R+h

6. Limites de Integração L 0 y x z No eixo y - os limites são 0 e L

7. Limites de Integração h 0 y x z -R+h No eixo z - os limites são -R e -R+h -R

8. Limites de Integração 0 y x z No eixo x os limites são e

9. Limites de Integração Como, e Temos que:  

10. Obtendo a integral tripla (Por simetria)

11. Resolvendo a integral tripla por coordenadas cartesianas

12. Para resolver a integral acima, é necessário que façamos uso da técnica de substituição trigonométrica

13. Utilizando substituição trigonométrica

25. Para: 0  h  2R; L > 0; e R > 0.

26. Testando a validade da equação Há 3 pontos onde pode-se testar a validade da equação através da lógica e geometria espacial: Quando h=0; Quando h=R; (Meio Cilindro) Quando h=2R (Cilindro inteiro).

27. Quando h=0

28. Quando h=R (Meio Cilindro)

29. Quando h=2R (Cilindro Inteiro)

30. Obtendo a equação específica Para o cilindro utilizado na prática temos: R = 7,275 cm L = 29,8 cm Assim:

31. Medidas Realizadas Para comprovar na prática a equação, foi inserido um volume pré-definido de líquido no recipiente e medido a altura h. Foram realizadas 4 medidas: V=0 (Sem líquido) V=1L V=2L V=3L

32. Valores Obtidos Para V=0  h = 0; Para V=1L  h = 3,726 cm; Para V=2L  h = 6,17 cm; Para V=3L  h = 8,486 cm;

33. Volume Obtido Para h = 0  V=0; Para h = 3,726 cm  V = 1002,047 ml (esperado 1000 ml); Para h = 6,170 cm  V = 2000,166 ml (esperado 2000 ml); Para h = 8,486 cm  V = 3000,77 ml (esperado 3000 ml);

34. Fatores contribuintes para a margem de erro Erro de paralaxe na leitura; Deformações e/ou irregularidades na superfície; Precisão da escala do paquímetro; Possível inclinação do paquímetro na obtenção das medidas; Ângulo de contato formado entre o líquido e o vidro devido à tensão superficial, dependente das características do líquido utilizado;