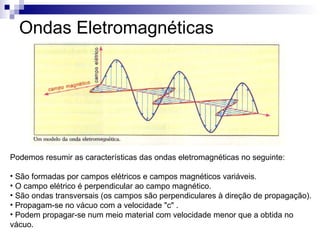
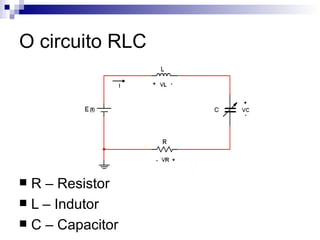
Este documento descreve como encontrar a equação da frequência ressonante em um circuito RLC usando equações diferenciais. Ele define as características das ondas eletromagnéticas e do espectro eletromagnético, e descreve como derivar a equação da frequência ressonante para um circuito RLC, resultando na equação ω0=1/√LC.

1. Utilizando Equações Diferenciais para Encontrar a Equação da Freqüência Ressonante em um Circuito RLC

2. Alunos: Carlos Eduardo Gonçalves Arantes Cassiano Germanovix de Oliveira Eduardo Rovanni do Nascimento Fábio da Silva Tesser Rodrigo de Jesus Godoy Curso: Engenharia Elétrica Disciplina: Cálculo III Professor: Valdemir Antunes Turma: 4º Semestre

3. Ondas Eletromagnéticas Podemos resumir as características das ondas eletromagnéticas no seguinte: São formadas por campos elétricos e campos magnéticos variáveis. O campo elétrico é perpendicular ao campo magnético. São ondas transversais (os campos são perpendiculares à direção de propagação). Propagam-se no vácuo com a velocidade "c" . Podem propagar-se num meio material com velocidade menor que a obtida no vácuo.

4. Espectro Eletromagnético

5. Polarização de Ondas Polarização Vertical (AM) Polarização Horizontal (TV) Polarização Inclinada Polarização Circular (Celulares)

6. Circuitos Ressonantes

7. Ondas de Rádio rádio AM - 525 kilohertz a 1.625 megahertz rádio de ondas curtas - 5.9 megahertz a 26.1 megahertz rádio CB - 26.96 megahertz a 27.41 megahertz canais de TV - 54 a 88 megahertz do canal 2 até o 6 rádio FM - 88 megahertz a 108 megahertz canais de TV - 174 a 220 megahertz do canal 7 até o 13

8. O circuito RLC R – Resistor L – Indutor C – Capacitor

9. Pela Lei de Kirchoff (1)

10. (2) (3) (4)

11. Substituindo as Equações (2),(3) e (4) na Equação (1) Dividindo ambos os lados por L, temos:

12. Simplificando a equação: Resultando na equação diferencial de 2º ordem linear homogênea:

13. Para o circuito LC ( R=0 e E(t)=0):

14. e, Obtêm-se Raízes Complexas (Caso 2), Cuja Solução é Dada por: Como só temos o termo imaginário das raízes, o termo a é igual a zero: (5)

15. Derivando-se a equação anterior, obtêm-se a equação da corrente: (6)

16. Utilizando-se como condições iniciais q(0)=q0 e i(0)=0, respectivamente nas equações 5 e 6:

17. Substituindo-se os valores de C 1 e C 2 na Equação 5, temos: Contudo, como: Verifica-se que: Têm-se que: [Hz] (7)

18. Determinando a faixa de freqüência ressonante para transmissões AM (Amplitude Modulada): Isolando o Capacitor na Equação 7: Faixa de Freqüência AM: 525 kHz – 1625 kHz Indutor Utilizado: 100 H = 100.10 -6 H [F]

19. Determinando a faixa de freqüência ressonante para transmissões AM (Amplitude Modulada): Para a freqüência de 525 kHz

20. Determinando a faixa de freqüência ressonante para transmissões AM (Amplitude Modulada): Para a freqüência de 1625 kHz

21. Determinando a faixa de freqüência ressonante para transmissões AM (Amplitude Modulada): Faixa de Freqüência AM: 525 kHz – 1625 kHz Indutor Utilizado: 100 H = 100.10 -6 H Faixa de Capacitância: 919 pF – 95,9 pF