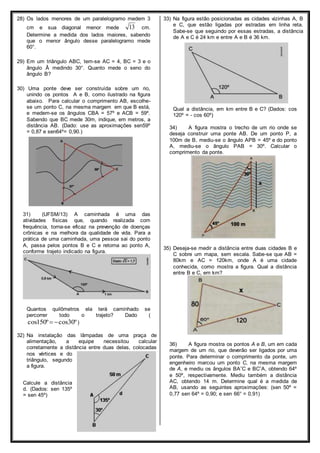
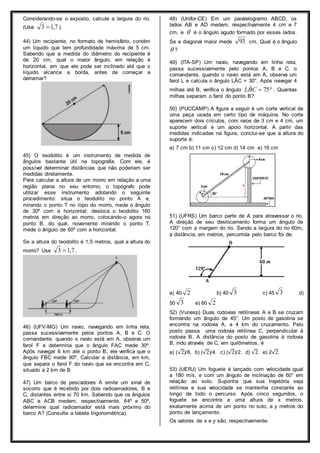
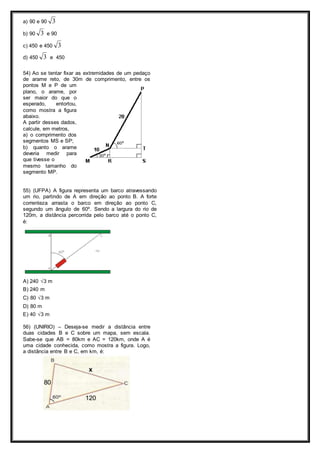
1) O documento apresenta exercícios sobre trigonometria no triângulo retângulo e no triângulo qualquer, incluindo definições de seno, cosseno e tangente de ângulos notáveis e aplicações destes conceitos na resolução de problemas. 2) São fornecidos exercícios para cálculo de lados e ângulos de triângulos retângulos e quaisquer, utilizando fórmulas trigonométricas e propriedades. 3) Inclui também exercícios sobre paralelogramos, trap

1. ALUNO (A): Vinícius Moço da Silva Nº ______
PROFESSOR: CLAUZIR PAIVA NASCIMENTO
DATA: 15/09/2014 TURMA: 9° ANO.
ATIVIDADE DE
MATEMÁTICA
1ª LISTA DE EXERCÍCIOS DO 3º TRIMESTRE: ESTUDO DA TRIGONOMETRIA
ASSUNTO RESUMO
Seno de um ângulo
c o
hip
sen
.

Cosseno de um ângulo
ac . .
hip
cos 
o c

. .
tan
Tangente de um ângulo c
. a .
cos
tan
sen

Lei dos senos
c
ˆ sen cˆ
b
sen b
a
sen â
 
Lei dos cossenos a b c 2 b c cosâ 2 2 2      
TABELA DE ÂNGULOS NOTÁVEIS
30° 45° 60°
SENO
1
2
2
2
3
2
COSSENO
3
2
2
2
1
2
TANGENTE
3
3
1 3
Se os ângulos forem complementares ( a + b = 90°)=> sen a = cos b
Se os ângulos forem suplementares (a + b = 180°)=> sen a = sen b e cos a = - cos b

2. TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO.
1) A hipotenusa BC de um triângulo retângulo mede 30
cm e o ângulo ABˆC mede 60°. Determine a medida
dos catetos.
2) Um avião se aproxima de um aeroporto A, em linha
reta. Ao atingir o ponto B, o piloto é avisado de que
deve alterar a sua rota para aterrissar em outro
aeroporto, C, distante 60 km de A.
Um mapa indica que a reta que liga A a C é
perpendicular à trajetória que o avião percorria, e o
piloto deve fazer um giro de 60° com o avião. Qual a
distância que o avião deverá percorrer para chegar a
C?
3) Um prédio foi construído de forma que sua porta de
entrada está 1,20 m acima do nível da calçada. O
arquiteto projetou uma rampa que ligará a calçada
à porta de entrada do prédio e terá uma inclinação
de 30° com a horizontal. Qual é o comprimento
dessa rampa?
4) Um barco navega em um rio, segundo uma linha
reta PQ, distante 20 m de uma das margens. Ao
atingir um ponto A, o piloto faz um giro de 120°
para a direita do movimento do barco e se dirige,
em linha reta, para um ponto B da margem. Calcule
a distância que separa A de B.
5) (UFG) Uma pessoa deseja subir uma rampa de
comprimento d que forma um angulo α com a
horizontal. Apos subir a rampa, esta pessoa estará
h metros acima da posição em que se encontrava
inicialmente, como mostra a figura abaixo.
a) Que relação existe entre os valores de α, h e d?
b) Supondo α = 30° e h = 1 m, qual o valor de d?
6) (Unifor-CE) Na figura abaixo tem-se um observador
O, que vê o topo de um prédio sob um ângulo de 45°.
A partir desse ponto, afastando-se do prédio 8 metros,
ele atinge o ponto A, de onde passa a ver o topo do
mesmo prédio sob um ângulo θ tal que
6
tg  .
7
Qual a altura do prédio?
7) Na figura, ABCD é um retângulo em que BD é uma
diagonal, AH é perpendicular a BD, AH  5 3 cm e
º 30   , calcule a área do retângulo em cm2.
8) (Fatec-SP) De dois observatórios,
localizados nos pontos X e Y da superfície da Terra,
e possível enxergar um balão meteorológico B, sob
ângulos de 45° e 60°, conforme e mostrado na figura
a seguir.
Desprezando-se a curvatura da Terra, se 30 km
separam X e Y, a altura h, em quilômetros, do balão
a superfície da Terra, é: (use 3 1,7) .

3. 9) Uma torre de transmissão de energia elétrica está
localizada em um terreno plano. Uma pessoa em
um ponto X a avista sob um ângulo de 60°. Ao se
afastar, segundo uma linha reta que liga a torre ao
ponto X, essa pessoa percebe que, após percorrer
20 m, avista a torre segundo um ângulo de 30°.
Qual é a altura da torre?
10) Em um triângulo retângulo ABC, de hipotenusa AC,
prolonga-se o cateto BC até um ponto D tal que C
está entre B e D e med BDˆA 30 . Calcule a
medida de CD, sabendo que o ângulo  do
triângulo mede 30° e AB  50 3 .
11) Uma praça tem forma triangular e é delimitada
pelas ruas Acre, Pará e Amazonas. Deseja-se abrir
uma passagem para ciclistas ligando a rua
Amazonas à rua Pará, perpendicularmente à rua
Amazonas. Qual deverá ser a largura dessa
passagem para que a abertura d (ver figura) na rua
Pará tenha no mínimo 2 m? (Se necessário, use
3 1,71 )
12) Em uma circunferência de raio 5 cm,
considere o diâmetro AB e a corda BC, de modo que
med (ABC) = 30°. Determine BC.
13) (Unic-MT) Uma escada de 5 metros de
comprimento esta encostada num muro vertical
formando com ele um angulo de 30°. Um homem, ao
subir nessa escada, observa que, devido a
problemas de aderência com o piso horizontal, esta
escorrega sem se afastar do muro e para no ponto
em que o angulo formado entre ela e o piso
horizontal e de 30°. Nessas condições, o
deslocamento efetuado pela escada junto ao muro
foi de:
a) 1,85 m b) 2,50 m c) 5,00 m d) 0,85 m e) 4,35 m
14) (Vunesp-SP) Um pequeno avião deveria partir de
uma cidade A rumo a uma cidade B ao norte,
distante 60 quilômetros de A. Por um problema de
orientação, o piloto seguiu erradamente rumo ao
oeste. Ao perceber o erro, ele corrigiu a rota,
fazendo um giro de 120° a direita em um ponto C,
de modo que o seu trajeto, juntamente com o
trajeto que deveria ter sido seguido, formaram,
aproximadamente, um triangulo retângulo ABC,
como mostra a figura.
15) A ranhura trapezoidal e utilizada na
construção de guias para elementos de maquinas. A
mais comum e a ranhura conhecida como rabo de
andorinha, indicada na figura. Determine os valores
(aproximados) de x e y.
16) (Cefet-PR) Se na figura ao lado AB = 9 cm, o
segmento DF mede, em centímetros:
a) 5 b) 4 c) 8 d) 7 e) 6

4. 17) (Faap-SP) A soma dos comprimentos das bases de
um trapézio retângulo vale 30 m. A base maior
mede o dobro da menor. Calcule a altura do
trapézio, sabendo que seu angulo agudo mede 30°.
18) Num triangulo retângulo, a tangente de um dos
ângulos agudos e 1,05 e a soma dos comprimentos
dos catetos e 41 cm. Qual o comprimento da
hipotenusa desse triangulo?
19) (UFPB) Em parques infantis, é comum encontrar um
brinquedo, chamado escorrego, constituído de uma
superfície plana inclinada e lisa (rampa), por onde as
crianças deslizam, e de uma escada que dá acesso à
rampa. No parque de certa praça, há um escorrego,
apoiado em um piso plano e horizontal, cuja escada
tem 2 m de comprimento e forma um ângulo de 45º
com o piso; e a rampa forma um ângulo de 30º com o
piso, conforme ilustrado na figura a seguir.
20) Em um shopping, uma pessoa sai do primeiro
pavimento para o segundo através de uma escada
rolante, conforme a figura a seguir.
A altura H, em metros, atingida pela pessoa, ao chegar
ao segundo pavimento, é:
a) 15 b) 10 c) 5 d) 3 e) 2
21) Um homem viaja de ônibus em uma estrada com um
longo trecho MN em linha reta ao lado de um campo.
Ao passar por um ponto A, ele avista uma casa C, de
modo que o ângulo CÂN mede 60°. Após percorrer
600 m, ele está em um ponto E e vê a casa de forma
que CÊN mede 135°. Calcule a distância que a casa
está da estrada. (Se necessário, use 2 1,41e
3 1,73 ).
22) Uma escada rolante de 6 metros de comprimento
liga dois andares de uma loja e tem inclinação de
30º. Determine, em metros, a altura entre estes
dois andares.
23) As circunferências da figura abaixo são tangentes
entre si e tangentes a reta t nos pontos A e B.
Dados:
BC = 3 4 cm
R = 12
Qual a medida do segmento AB?
24) Um atleta se desloca com velocidade de 10 km/h
ao longo da reta OP, que forma um ângulo de 30º
com a reta Ox, partindo do ponto O. Após 3 horas,
qual a distância do atleta até a reta Ox?
25) Um prédio hospitalar está sendo construído em um
terreno declivoso. Para otimizar a construção, o
arquiteto responsável idealizou o estacionamento
no subsolo do prédio, com entrada pela rua dos
fundos do terreno. A recepção do hospital está 5
metros acima do nível do estacionamento, sendo
necessária a construção de uma rampa retilínea de
acesso para os pacientes com dificuldades de
locomoção. A figura representa esquematicamente
esta rampa (r), ligando o ponto A, no piso da
recepção, ao ponto B, no piso do estacionamento,
a qual deve ter uma inclinação α mínima de 30º e
máxima de 45º.
Nestas condições e considerando 2 1,4 , quais
deverão ser os valores máximo e mínimo, em
metros, do comprimento desta rampa de acesso?
TRIGONOMETRIA EM UM TRIÂNGULO
QUALQUER.
26) Os lados de um triângulo medem 6 cm, 8 cm e 12
cm. Calcule o cosseno do maior ângulo interno
desse triângulo.
27) Calcule o cosseno do maior ângulo de um triângulo
de lados 12 cm, 15 cm e 18 cm.

5. 28) Os lados menores de um paralelogramo medem 3
cm e sua diagonal menor mede 13 cm.
Determine a medida dos lados maiores, sabendo
que o menor ângulo desse paralelogramo mede
60°.
29) Em um triângulo ABC, tem-se AC = 4, BC = 3 e o
ângulo  medindo 30°. Quanto mede o seno do
ângulo B?
30) Uma ponte deve ser construída sobre um rio,
unindo os pontos A e B, como ilustrado na figura
abaixo. Para calcular o comprimento AB, escolhe-se
um ponto C, na mesma margem em que B está,
e medem-se os ângulos CBA = 57º e ACB = 59º.
Sabendo que BC mede 30m, indique, em metros, a
distância AB. (Dado: use as aproximações sen59º
= 0,87 e sen64º= 0,90.)
31) (UFSM/13) A caminhada é uma das
atividades físicas que, quando realizada com
frequência, torna-se eficaz na prevenção de doenças
crônicas e na melhora da qualidade de vida. Para a
prática de uma caminhada, uma pessoa sai do ponto
A, passa pelos pontos B e C e retorna ao ponto A,
conforme trajeto indicado na figura.
Quantos quilômetros ela terá caminhado se
percorrer todo o trajeto? Dado (
cos150º cos30º )
32) Na instalação das lâmpadas de uma praça de
alimentação, a equipe necessitou calcular
corretamente a distância entre duas delas, colocadas
nos vértices e do
triângulo, segundo
a figura.
Calcule a distância
d. (Dados: sen 135º
= sen 45º)
33) Na figura estão posicionadas as cidades vizinhas A, B
e C, que estão ligadas por estradas em linha reta.
Sabe-se que seguindo por essas estradas, a distância
de A e C é 24 km e entre A e B é 36 km.
Qual a distância, em km entre B e C? (Dados: cos
120º = - cos 60º)
34) A figura mostra o trecho de um rio onde se
deseja construir uma ponte AB. De um ponto P, a
100m de B, mediu-se o ângulo APB = 45º e do ponto
A, mediu-se o ângulo PAB = 30º. Calcular o
comprimento da ponte.
35) Deseja-se medir a distância entre duas cidades B e
C sobre um mapa, sem escala. Sabe-se que AB =
80km e AC = 120km, onde A é uma cidade
conhecida, como mostra a figura. Qual a distância
entre B e C, em km?
36) A figura mostra os pontos A e B, um em cada
margem de um rio, que deverão ser ligados por uma
ponte. Para determinar o comprimento da ponte, um
engenheiro marcou um ponto C, na mesma margem
de A, e mediu os ângulos BAˆC e BCˆA, obtendo 64º
e 50º, respectivamente. Mediu também a distância
AC, obtendo 14 m. Determine qual é a medida de
AB, usando as seguintes aproximações: (sen 50º =
0,77 sen 64º = 0,90; e sen 66° = 0,91)

6. 37) Dois amigos, André e Bruno, estão num
campo aberto empinando pipa. Eles estão,
respectivamente, nas posições A e B. Os fios dessas
pipas se enroscam e se rompem, fazendo com que
as duas pipas caiam juntas num ponto C, distante 40
m de André. A distância de Bruno ate as pipas é:
38) (UFG-GO) Uma empresa de engenharia deseja
construir uma estrada ligando os pontos A e B, que
estão situados em lados opostos de uma reserva
florestal, como mostra a figura a seguir.
A empresa optou por construir dois trechos retilíneos,
denotados pelos segmentos AC e CB, ambos com o
mesmo comprimento. Considerando que a distância de
A até B, em linha reta, é igual ao dobro da distância de
B a D, o ângulo á, formado pelos dois trechos retilíneos
da estrada, mede:
a) 110º b) 120º c) 130º d) 140º d) 150º
39) (CESGRANRIO) No triângulo ABC, os lados
AC e BC medem 8cm e 6cm, respectivamente, e o
ângulo A vale 30°. O seno do ângulo B vale:
a) ½ b) 2/3 c) ¾ d) 4/5 e) 5/6
40) A figura representa um mapa em escala 1 : 1000,
indicando três pontos em uma selva. Os lados do
triângulo representam os possíveis caminhos para
deslocar-se entre esses pontos. Um grupo de amigos
está na posição representada pelo ponto A. Quanto
eles irão percorrer para chegar à posição representada
pelo ponto C, sabendo que utilizarão o caminho mais
curto?
41) Um observador, situado no ponto A, distante 30 m
do ponto B, vê um edifício sob um ângulo de 30°,
conforme a figura. Baseado nos dados da figura
determine a altura do edifício em metros e divida o
resultado por 2
a) 10 m
b) 11 m
c) 12 m
d) 14 m
e) 15 m
42) Um grupo de escoteiros pretende escalar uma
montanha ate o topo, representado na figura abaixo
pelo ponto D, visto sob ângulos de 40° do
acampamento B e de 60° do acampamento A.
Dado: sen 20º = 0,342
Considerando que o percurso de 160 m entre A e B e
realizado segundo um angulo de 30° em relação a base
da montanha, então, a distância entre B e D, em m, e
de, aproximadamente,
a) 190. b) 234. c) 260. d) 320.
EXERCÍCIOS DIVERSOS.
43) (UFG/13) Um topógrafo deseja calcular a largura
de um rio em um trecho onde suas margens são
paralelas e retilíneas. Usando como referência uma
árvore, A, que está na margem oposta, ele
identificou dois pontos B e C, na margem na qual se
encontra, tais que os ângulos ABC e ACB medem
135° e 30°, respectivamente. O topógrafo, então,
mediu a distância entre B e C, obtendo 20 metros.

7. Considerando-se o exposto, calcule a largura do rio.
(Use 3 1,7 ).
44) Um recipiente, no formato de hemisfério, contém
um líquido que tem profundidade máxima de 5 cm.
Sabendo que a medida do diâmetro do recipiente é
de 20 cm, qual o maior ângulo, em relação à
horizontal, em que ele pode ser inclinado até que o
líquido alcance a borda, antes de começar a
derramar?
45) O teodolito é um instrumento de medida de
ângulos bastante útil na topografia. Com ele, é
possível determinar distâncias que não poderiam ser
medidas diretamente.
Para calcular a altura de um morro em relação a uma
região plana no seu entorno, o topógrafo pode
utilizar esse instrumento adotando o seguinte
procedimento: situa o teodolito no ponto A e,
mirando o ponto T no topo do morro, mede o ângulo
de 30º com a horizontal; desloca o teodolito 160
metros em direção ao morro, colocando-o agora no
ponto B, do qual, novamente mirando o ponto T,
mede o ângulo de 60º com a horizontal.
Se a altura do teodolito é 1,5 metros, qual a altura do
morro? Use 3 1,7 .
46) (UFV-MG) Um navio, navegando em linha reta,
passa sucessivamente pelos pontos A, B e C. O
comandante, quando o navio está em A, observa um
farol F e determina que o ângulo FAC mede 30º.
Após navegar 6 km até o ponto B, ele verifica que o
ângulo FBC mede 90º. Calcular a distância, em km,
que separa o farol F do navio que se encontra em C,
situado a 2 km de B
47) Um barco de pescadores A emite um sinal de
socorro que é recebido por dois radioamadores, B e
C, distantes entre si 70 km. Sabendo que os ângulos
ABC e ACB medem, respectivamente, 64º e 50º,
determine qual radioamador está mais próximo do
barco A? (Consulte a tabela trigonométrica).
48) (Unifor-CE) Em um paralelogramo ABCD, os
lados AB e AD medem, respectivamente 4 cm e 7
cm, e  é o ângulo agudo formado por esses lados.
Se a diagonal maior mede 93 cm, Qual é o ângulo
 ?
49) (ITA-SP) Um navio, navegando em linha reta,
passa sucessivamente pelo pontos A, B e C. o
comandante, quando o navio está em A, observa um
farol L e calcula o ângulo LÂC = 30°. Após navegar 4
milhas até B, verifica o ângulo   75 ˆCBL . Quantas
milhas separam o farol do ponto B?
50) (PUCCAMP) A figura a seguir é um corte vertical de
uma peça usada em certo tipo de máquina. No corte
aparecem dois círculos, com raios de 3 cm e 4 cm, um
suporte vertical e um apoio horizontal. A partir das
medidas indicadas na figura, conclui-se que a altura do
suporte é:
a) 7 cm b) 11 cm c) 12 cm d) 14 cm e) 16 cm
51) (UFRS) Um barco parte de A para atravessar o rio.
A direção de seu deslocamento forma um ângulo de
120° com a margem do rio. Sendo a largura do rio 60m,
a distância, em metros, percorrida pelo barco foi de:
a) 40 2 b) 40 3 c) 45 3 d)
50 3 e) 60 2
52) (Vunesp) Duas rodovias retilíneas A e B se cruzam
formando um ângulo de 45°. Um posto de gasolina se
encontra na rodovia A, a 4 km do cruzamento. Pelo
posto passa uma rodovia retilínea C, perpendicular à
rodovia B. A distância do posto de gasolina à rodovia
B, indo através de C, em quilômetros, é
a) (√2)/8. b) (√2)/4. c) (√2)/2. d) √2. e) 2√2.
53) (UERJ) Um foguete é lançado com velocidade igual
a 180 m/s, e com um ângulo de inclinação de 60° em
relação ao solo. Suponha que sua trajetória seja
retilínea e sua velocidade se mantenha constante ao
longo de todo o percurso. Após cinco segundos, o
foguete se encontra a uma altura de x metros,
exatamente acima de um ponto no solo, a y metros do
ponto de lançamento.
Os valores de x e y são, respectivamente:

8. a) 90 e 90 3
b) 90 3 e 90
c) 450 e 450 3
d) 450 3 e 450
54) Ao se tentar fixar as extremidades de um pedaço
de arame reto, de 30m de comprimento, entre os
pontos M e P de um
plano, o arame, por
ser maior do que o
esperado, entortou,
como mostra a figura
abaixo.
A partir desses dados,
calcule, em metros,
a) o comprimento dos
segmentos MS e SP;
b) quanto o arame
deveria medir para
que tivesse o
mesmo tamanho do
segmento MP.
55) (UFPA) A figura representa um barco atravessando
um rio, partindo de A em direção ao ponto B. A forte
correnteza arrasta o barco em direção ao ponto C,
segundo um ângulo de 60º. Sendo a largura do rio de
120m, a distância percorrida pelo barco até o ponto C,
é:
A) 240 √3 m
B) 240 m
C) 80 √3 m
D) 80 m
E) 40 √3 m
56) (UNIRIO) – Deseja-se medir a distância entre
duas cidades B e C sobre um mapa, sem escala.
Sabe-se que AB = 80km e AC = 120km, onde A é
uma cidade conhecida, como mostra a figura. Logo,
a distância entre B e C, em km, é: