O documento aborda conceitos fundamentais de vetores, matrizes e transformações lineares, incluindo definições, notações e operações matemáticas relevantes. Explora a interpretação geométrica das transformações, como rotação e escala, enfatizando a representação matriz das transformações. Além disso, discute as vantagens de diferentes representações de vetores e a importância de compreender como as matrizes afetam as transformações de objetos e coordenadas.

1. Vetores (cont), Matrizes e
Transformações Lineares
Anderson Tavares
acmt@ecomp.poli.br
Grupo de Estudo em Ambientes Virtuais
geav.ecomp.poli.br

2. Definição Matemática
• Notações
Exemplo de Matriz Índices (linha e coluna)
Matriz Diagonal Matriz Identidade
Diagonal Principal

3. Definição Matemática
• Vetores como Matrizes
Vetor Linha (1 x n) Vetor Coluna (n x 1)
Matriz Transposta Matriz Transposta

4. Definição Matemática
• Vetores como Matrizes
Transposta de vetor linha Transposta de vetor coluna

5. Definição Matemática
• Multiplicar matriz por escalar

6. Definição Matemática
• Produto de Matrizes
Devem ser
iguais colunas do resultado
linhas do resultado
Cada termo é o produto escalar do vetor linha i com o vetor coluna j

7. Definição Matemática
• Produto de Matrizes
Outra maneira de reescrever as matrizes

8. Definição Matemática
• Exemplo

9. Definição Matemática
• Exemplo

10. Definição Matemática
• Obs: Matriz M x Matriz quadrada S
– I,j x j,j = l,j
– l,l x l,j = l,j
– M x I = I x M = M (I = Matriz Identidade)
– AB ≠ BA (Não é comutativa)
– (AB)C = A(BC) (É associativa)
– (kA)B = k(AB) = A(kB)
– (vA)B = v(AB)
– (AB)T = BTAT

11. Definição Matemática
Indefinido
Indefinido

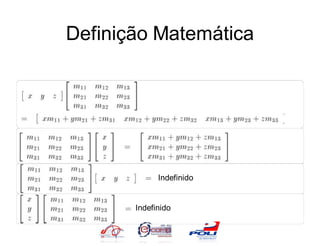
12. Definição Matemática
• Vantagens (Vetores Linhas)
– Mais fácil escrever [4,5,6] do que
– Leitura Natural
– DirectX usa
• Vantagens (Vetores Coluna)
– Equações (Ex: ABCv parece A(B(C(v))))
– Livros de álgebra linear adotam
– Livros de Computação Gráfica adotam
– OpenGL usa

13. Interpretação Geométrica
• Descreve uma transformação linear
• Pode “esticar”, porém não pode curvar ou
distorcer o espaço
• Rotação
• Escala
• Projeção Ortográfica
• Reflexão
• Shearing (Skewing)

14. Interpretação Geométrica
• Como uma matriz transforma vetores

15. Interpretação Geométrica
• O que uma matriz parece?
Cada linha da matriz pode ser vista como vetor base após a transformação

16. Interpretação Geométrica
• Implicações
– Podemos ver uma matriz e visualizar que
transformação ela faz.
– Podemos fazer uma transformação reversa
• Um exemplo:

17. Interpretação Geométrica

18. Interpretação Geométrica
• Para facilitar

19. Interpretação Geométrica
• Transformação em 3D

20. • Exercícios
– Que transformação essa matriz faz?
– Reexpresse sem os parênteses

21. Transformações Lineares
• Transformar um objeto é uma coisa

22. Transformações Lineares
• Transformar a coordenada é outra

23. Transformações Lineares
• Exemplo de rotação da coordenada

24. Transformações Lineares
• Transf. objeto = - Transf. coordenada

25. Rotação
• Rotação em 2D

26. Rotação
• Rotação em 3D sobre eixos cardinais

27. Rotação
• Rotação no eixo X

28. Rotação
• Rotação no eixo Y

29. Rotação
• Rotação no eixo Z

30. Rotação
• Rotação sobre qualquer eixo
– Tomem um café e se alongue antes
– Queremos girar um vetor v qualquer, θ graus,
num eixo n
– Transformar v em dois vetores
• Perpendicular
• Paralelo

31. Rotação
• v|| é paralelo a n (projetado).
Então v || é (v·n)n.
• v ┴ é perpendicular a n. Então
é v ┴ = v – v ||
• w (um vetor de referência) é
perpendicular a v ┴ e n (e
mesmo comprimento de v ┴.)
Então é w = nv ┴

32. Rotação

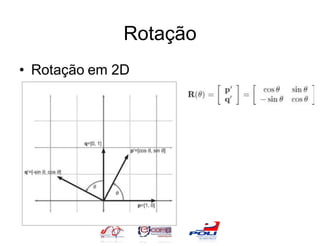
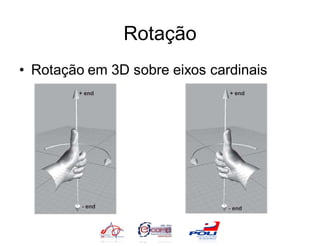
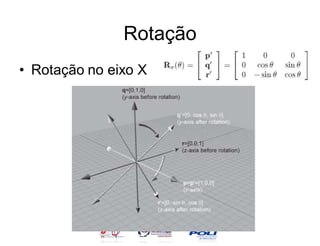
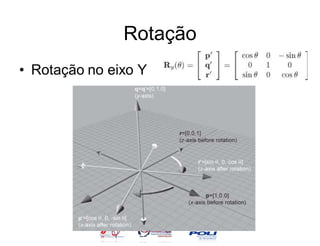
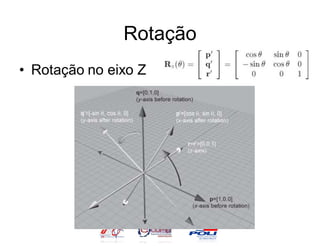
33. Rotação
• Iremos agora compor nossa matriz
– Lembre-se: a matriz representa o conjunto de
vetores base após a transformação
– Então iremos usar
• v = [1,0,0]
• v = [0,1,0]
• v = [0,0,1]
– Computar v’ de cada vetor base e juntar para
fazer a matriz.

34. Rotação

35. Rotação
• Outros vetores-base
– (calcula da mesma forma)

36. Rotação
• Tendo os 9 números, podemos compor a
nossa matriz