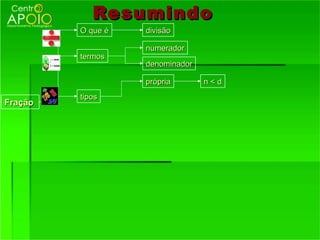
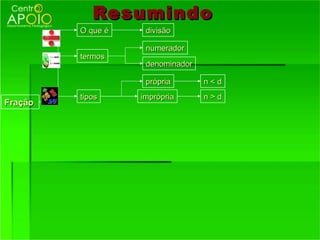
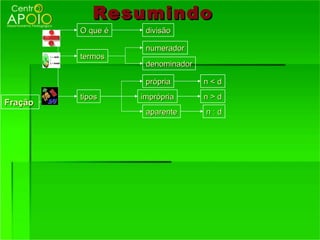
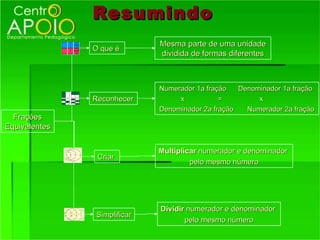
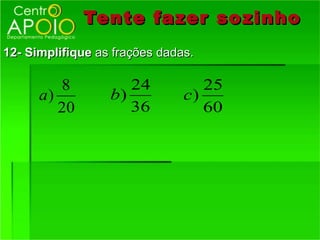
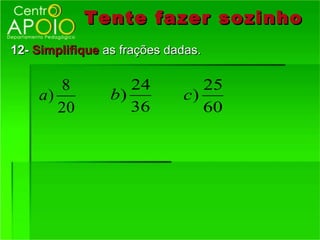
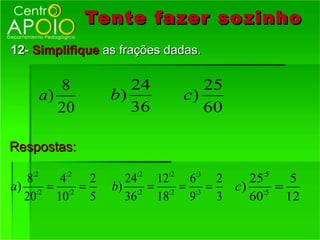
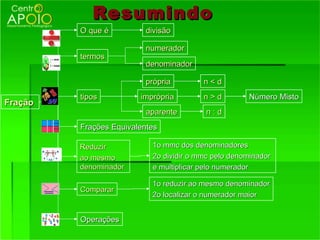
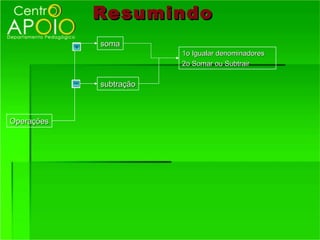
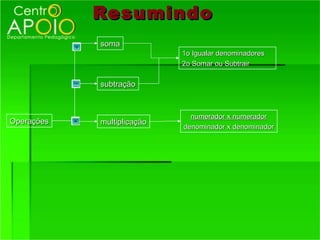
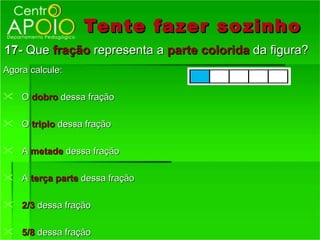
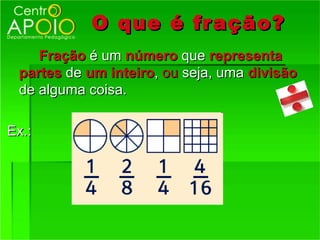
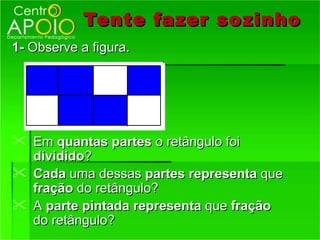
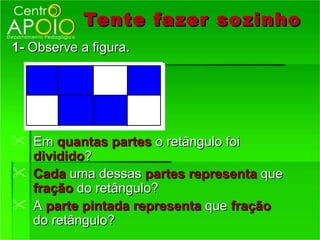
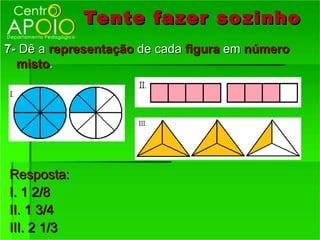
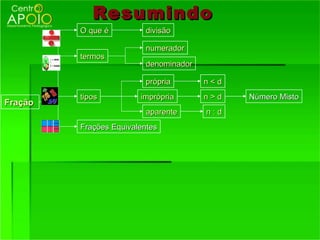
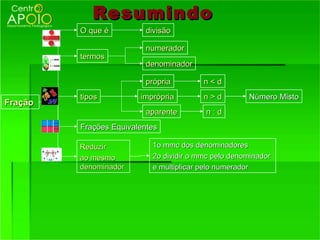
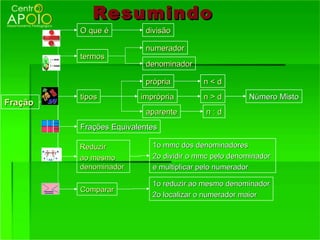
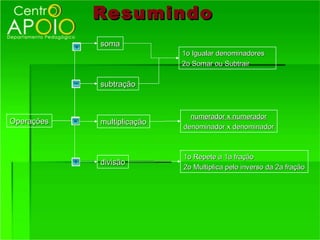
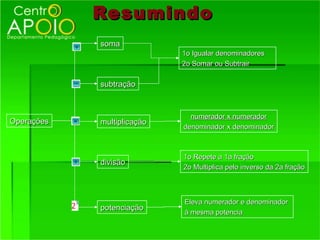
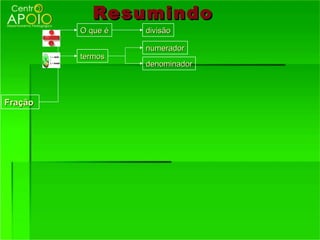
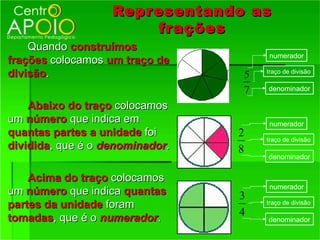
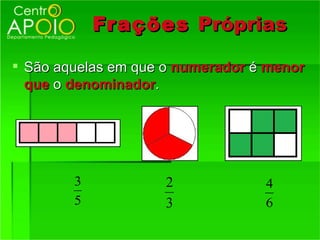
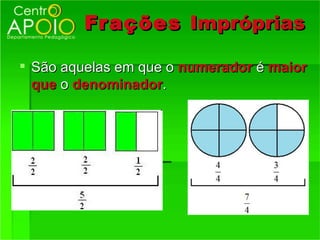
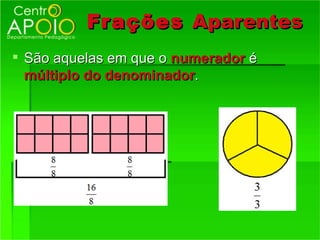
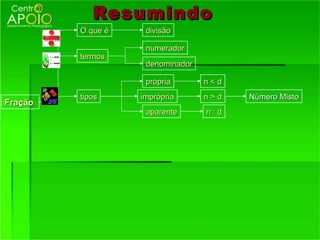
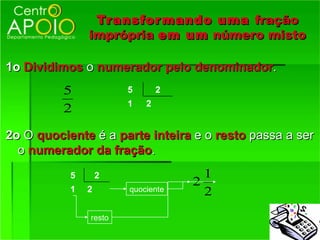
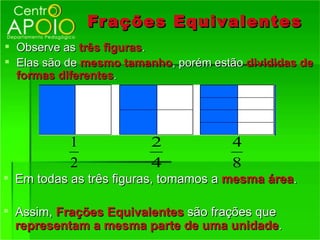
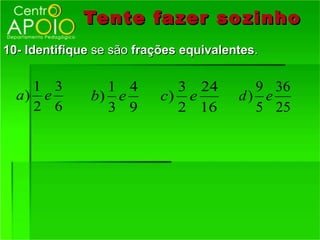
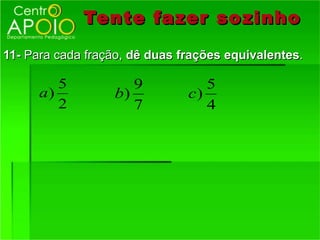
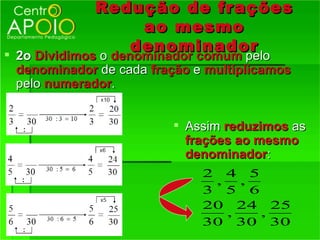
O documento fornece informações sobre frações, incluindo: 1) O que são frações e como funcionam, representando partes de um todo; 2) Os termos de uma fração - numerador e denominador; 3) Como reconhecer frações equivalentes, multiplicando os termos correspondentes.

2. O que você
precisa saber
 As quatro operações básicas (soma, subtração,
multiplicação e divisão)
 Múltiplos de um número
 Mínimo mútiplo comum (mmc)
 Potência

3. O que é fr ação?
Fração é um número que representa
partes de um inteiro, ou seja, uma divisão
de alguma coisa.
Ex.:

4. Resumindo
O que é divisão
Fração

5. Como funciona?
 Temos uma circunferência repartida em três
partes.
 Cada parte representa 1/3 dessa circunferência,
assim, somando as três, temos 3/3, ou 1 inteira.
1 1 1 3
=1
3 3 3 3

6. Ter mos de uma
fr ação
O numerador e o denominador são os
termos da fração.

7. Resumindo
O que é divisão
numerador
termos
denominador
Fração

8. Repr esentando as
fr ações
Quando construímos
numerador
frações colocamos um traço de
divisão. 5 traço de divisão
7 denominador
Abaixo do traço colocamos
um número que indica em numerador
quantas partes a unidade foi 2 traço de divisão
dividida, que é o denominador. 8
denominador
Acima do traço colocamos
numerador
um número que indica quantas 3
partes da unidade foram traço de divisão
tomadas, que é o numerador. 4
denominador

9. Tente fazer so zinho
1- Observe a figura.
 Em quantas partes o retângulo foi
dividido?
 Cada uma dessas partes representa que
fração do retângulo?
 A parte pintada representa que fração
do retângulo?

10. Tente fazer so zinho
1- Observe a figura.
 Em quantas partes o retângulo foi
dividido?
 Cada uma dessas partes representa que
fração do retângulo?
 A parte pintada representa que fração
do retângulo?

11. Tente fazer
so zinho
1- Observe a figura.
 Em quantas partes o retângulo foi
dividido? R: 8 partes.
 Cada uma dessas partes representa que
fração do retângulo? R: 1/8.
 A parte pintada representa que fração
do retângulo? R: 5/8.

12. Tente fazer so zinho
2- Diga qual a fração que representa cada
bandeira.

13. Tente fazer so zinho
2- Diga qual a fração que representa cada
bandeira.

14. Tente fazer so zinho
2- Diga qual a fração que representa cada
bandeira.
 Resposta
a) 1/8 c) 4/8 e) 2/3
b) 2/6 d) 1/8 f) 1/4

15. Tente fazer so zinho
3- José, João e Celina representam 1/4 do total de
empregados do sítio de seu Gustavo. Quantos são
os empregados desse sítio?

16. Tente fazer so zinho
3- José, João e Celina representam 1/4 do total de
empregados do sítio de seu Gustavo. Quantos são
os empregados desse sítio?

17. Tente fazer so zinho
3- José, João e Celina representam 1/4 do total de
empregados do sítio de seu Gustavo. Quantos são
os empregados desse sítio?
 Resposta
1
.x = 3 ¼ do total de empregados = 3 empregados.
4
1.x = 3.4
Faremos a operação inversa.
x = 12

18. Tente fazer so zinho
4- Calcule quanto é:
1
a ) de20 =
4
5
b) de14
7

19. Tente fazer so zinho
4- Calcule quanto é:
1
a ) de20 =
4
5
b) de14
7

20. Tente fazer so zinho
4- Calcule quanto é:
1 1 20.1 20
a ) de20 = .20 = = =5
4 4 4 4
5 5 5.14 70
b) de14 .14 = = = 10
7 7 7 7

21. Tipos de Fr ações
 Próprias
 Impróprias
 Aparentes

22. Fr ações Próprias
 São aquelas em que o numerador é menor
que o denominador.
3 2 4
5 3 6

23. Resumindo
O que é divisão
numerador
termos
denominador
própria n<d
tipos
Fração

24. Fr ações Impróprias
 São aquelas em que o numerador é maior
que o denominador.

25. Resumindo
O que é divisão
numerador
termos
denominador
própria n<d
tipos imprópria n>d
Fração

26. Fr ações Aparentes
 São aquelas em que o numerador é
múltiplo do denominador.

27. Resumindo
O que é divisão
numerador
termos
denominador
própria n<d
tipos imprópria n>d
Fração
aparente n:d

28. Tente fazer so zinho
5- Classifique as frações como próprias, impróprias
ou aparentes.
2 9
a) 8 1 g)
8 b) 5 4 f) 1
2 c) 6 e) 9
6 d) 4
5

29. Tente fazer so zinho
5- Classifique as frações como próprias, impróprias
ou aparentes.
2 9
a) 8 1 g)
8 b) 5 4 f) 1
2 c) 6 e) 9
6 d) 4
5

30. Tente fazer so zinho
5- Classifique as frações como próprias, impróprias
ou aparentes.
2 9
a) 8 1 g)
8 b) 5 4 f) 1
2 c) 6 e) 9
6 d) 4
5
Resposta:
a) própria b) aparente c) própria d) imprópria
e) aparente f) própria g) aparente

31. Tente fazer so zinho
6- Observe as três figuras:
a) Que fração representa as partes coloridas
em cada figura?
b) Classifique essas frações como próprias,
impróprias ou aparentes.

32. Tente fazer
so zinho
6- Observe as três figuras:
a) Que fração representa as partes coloridas
em cada figura?
b) Classifique essas frações como próprias,
impróprias ou aparentes.

33. Tente fazer
so zinho
6- Observe as três figuras:
a) Que fração representa as partes coloridas
em cada figura?
R: I. 4/4 ou 1 inteiro, II. 3/4, III. 7/4
b) Classifique essas frações como próprias,
impróprias ou aparentes.
R: I. aparente, II. própria, III. imprópria

34. Númer o Misto
Representamos um número misto quando
há uma parte inteira e outra fracionada.

35. Resumindo
O que é divisão
numerador
termos
denominador
própria n<d
tipos imprópria n>d Número Misto
Fração
aparente n:d

36. Resumindo
O que é Parte inteira + fracionada
Número
Misto

37. Tente fazer so zinho
7- Dê a representação de cada figura em número
misto.

38. Tente fazer so zinho
7- Dê a representação de cada figura em número
misto.

39. Tente fazer so zinho
7- Dê a representação de cada figura em número
misto.
Resposta:
I. 1 2/8
II. 1 3/4
III. 2 1/3

40. Tr ansfor mando um número
Transfor
misto em uma fração imprópria
1o Transforme a parte inteira em fração aparente, utilizando o
mesmo denominador da parte fracionária.
2
1
3
3 2
+
3 3
2o Ficando as duas partes com denominadores iguais, agora
basta somar.
2 3 2 5
1 = + =
3 3 3 3

41. Resumindo
O que é Parte inteira + fracionada
Número
1o Transformar parte inteira em
misto fração aparente
Número 
Misto Fração 2o Somar as frações
imprópria
Transformar

42. Tente fazer so zinho
8- Tranforme cada número misto para fração
imprópria.
2 2 1 1 5
a )1 b) 4 c)2 d )2 e)3
7 7 3 2 11

43. Tente fazer so zinho
8- Tranforme cada número misto para fração
imprópria.
2 2 1 1 5
a )1 b) 4 c)2 d )2 e)3
7 7 3 2 11

44. Tente fazer so zinho
8- Tranforme cada número misto para fração
imprópria.
2 2 1 1 5
a )1 b) 4 c)2 d )2 e)3
7 7 3 2 11
Respostas:
7 2 9 7 2 30 3 1 7
a) + = b ) 4. + = c ) 2. + =
7 7 7 7 7 7 3 3 3
2 1 5 11 5 38
d ) 2. + = e)3. + =
2 2 2 11 11 11

45. Transfor mando uma fração
imprópria em um número misto
1o Dividimos o numerador pelo denominador.
5 5 2
1 2
2
2o O quociente é a parte inteira e o resto passa a ser
o numerador da fração.
5 2 1
2
1 2 quociente 2
resto

46. Resumindo
O que é Parte inteira + fracionada
Número
1o Transformar parte inteira em
misto fração aparente
Número 
Misto Fração 2o Somar as frações
imprópria
Transformar
Fração
1o Dividir numerador : denominador
imprópria

2o Quociente = inteiro,
Número
Resto = numerador
misto

47. Tente fazer
so zinho
9- Tranforme cada número misto para fração
imprópria.
18 15 7 23 10
a) b) c) d) e)
7 2 5 3 3

48. Tente fazer
sozinho
9- Tranforme cada número misto para fração
imprópria.
18 15 7 23 10
a) b) c) d) e)
7 2 5 3 3

49. Tente fazer so zinho
9- Tranforme cada número misto para fração
imprópria.
18 15 7 23 10
a) b) c) d) e)
7 2 5 3 3
Respostas:
18 7 15 2 7 5 23 3 10 3
4 2 1 7 2 1 2 7 1 3
4 1 2 2 1
a)2 b )7 c )1 d )7 e)3
7 2 5 3 3

50. Fr ações Equivalentes
 Observe as três figuras.
 Elas são de mesmo tamanho, porém estão divididas de
formas diferentes.
1 2 4
2 4 8
 Em todas as três figuras, tomamos a mesma área.
 Assim, Frações Equivalentes são frações que
representam a mesma parte de uma unidade.

51. Resumindo
O que é divisão
numerador
termos
denominador
própria n<d
tipos imprópria n>d Número Misto
Fração
aparente n:d
Frações Equivalentes

52. Resumindo
Mesma parte de uma unidade
O que é
dividida de formas diferentes
Frações
Equivalentes

53. Como r econhecer Fr ações
Equivalentes?
 Precisamos saber se 9/12 e 6/8 são equivalentes.
1o Multiplicamos o numerador da primeira fração pelo
denominador da segunda fração. 9 6
12 8
2o Multiplicamos o denominador da primeira fração pelo
numerador da segunda fração.
9 6
12 8
3o Comparamos os resultados. Se forem iguais, as
frações são equivalentes. 9 x8 = 72 9 6
=
12 x6 = 72 12 8

54. Resumindo
Mesma parte de uma unidade
O que é
dividida de formas diferentes
Numerador 1a fração Denominador 1a fração
Reconhecer x = x
Denominador 2a fração Numerador 2a fração
Frações
Equivalentes

55. Tente fazer so zinho
10- Identifique se são frações equivalentes.
1 3 1 4 3 24 9 36
a) e b) e c) e d) e
2 6 3 9 2 16 5 25

56. Tente fazer so zinho
10- Identifique se são frações equivalentes.
1 3 1 4 3 24 9 36
a) e b) e c) e d) e
2 6 3 9 2 16 5 25

57. Tente fazer sozinho
10- Identifique se são frações equivalentes.
1 3 1 4 3 24 9 36
a) e b) e c) e d) e
2 6 3 9 2 16 5 25
Respostas:
a) 1 x 6 = 6 b) 1 x 9 = 9 c) 3 x 16 = 48 d) 9 x 25 = 225
2x3=6 3 x 4 = 12 2 x 24 = 48 5 x 36 = 180
equivalentes não equivalentes não

58. Como criar Fr ações
Equivalentes?
 Temos a fração 4/7 e desejamos encontrar
frações equivalentes a ela.
x3 x4
x2
4 8 12 16
= = =
7 x2 14 21 28
x3
x4
 Multiplicamos numerador e denominador pelo
mesmo número.

59. Resumindo
Mesma parte de uma unidade
O que é
dividida de formas diferentes
Numerador 1a fração Denominador 1a fração
Reconhecer x = x
Denominador 2a fração Numerador 2a fração
Frações
Equivalentes
Multiplicar numerador e denominador
Criar
pelo mesmo número

60. Tente fazer so zinho
11- Para cada fração, dê duas frações equivalentes.
5 9 5
a) b) c)
2 7 4

61. Tente fazer so zinho
11- Para cada fração, dê duas frações equivalentes.
5 9 5
a) b) c)
2 7 4

62. Tente fazer so zinho
11- Para cada fração, dê duas frações equivalentes.
5 9 5
a) b) c)
2 7 4
Respostas:
x2 x3 x2 x3 x3 x6
5 10 30 9 18 27 5 15 30
a) x 2 = x3 = b) = x2
= x3
c) = x 3 = x6
2 4 12 7 14 21 4 12 24

63. Simplificação de
Frações
 Temos a fração 24/36 e pretendemos simplificá-la.
:3
:2
:2
24 12 6 2
= = = Tornou-se irredutível
36: 2 18 9 3
:2
:3
 Dividimos numerador e denominador pelo
mesmo número.
 Quando ela não pode mais ser simplificada (ou
reduzida) dizemos que ela é irredutível.

64. Resumindo
Mesma parte de uma unidade
O que é
dividida de formas diferentes
Numerador 1a fração Denominador 1a fração
Reconhecer x = x
Denominador 2a fração Numerador 2a fração
Frações
Equivalentes
Multiplicar numerador e denominador
Criar
pelo mesmo número
Dividir numerador e denominador
Simplificar
pelo mesmo número

65. Tente fazer so zinho
12- Simplifique as frações dadas.
8 24 25
a) b) c)
20 36 60

66. Tente fazer sozinho
12- Simplifique as frações dadas.
8 24 25
a) b) c)
20 36 60

67. Tente fazer so zinho
12- Simplifique as frações dadas.
8 24 25
a) b) c)
20 36 60
Respostas:
8:2 4:2 2 24:2 12:2 6:3 2 25:5 5
a ) :2 = :2 = b) :2 = :2 = :3 = c) :5 =
20 10 5 36 18 9 3 60 12

68. Redução de fr ações ao
mesmo denominador
Vamos obter frações equivalentes a 2/3, 4/5 e
5/6, de modo que todas tenham o mesmo
denominador.
 1o Calculamos o denominador comum as três
frações e múltiplo dos denominadores 3, 5 e 6 ao
mesmo tempo. Assim, estamos procurando o
mínimo múltiplo comum, ou seja, o mmc de 3, 5
e 6.
3 5 6 2
3 5 3 3  Obtemos o mmc igual a 30.
1 5 1 5
1 1 1 30

69. Redução de frações
ao mesmo
denominador
 2o Dividimos o denominador comum pelo
denominador de cada fração e multiplicamos
pelo numerador.
 Assim reduzimos as
frações ao mesmo
denominador:
2 4 5
, ,
3 5 6
20 24 25
, ,
30 30 30

70. Resumindo
O que é divisão
numerador
termos
denominador
própria n<d
tipos imprópria n>d Número Misto
Fração
aparente n:d
Frações Equivalentes
Reduzir 1o mmc dos denominadores
ao mesmo 2o dividir o mmc pelo denominador
denominador e multiplicar pelo numerador

71. Tente fazer so zinho
13- Reduza as frações a um mesmo denominador.
1 1 1 1 3 19 3 5 7
a) , e b) , e c) , e
2 3 4 5 7 70 4 6 10

72. Tente fazer so zinho
13- Reduza as frações a um mesmo denominador.
1 1 1 1 3 19 3 5 7
a) , e b) , e c) , e
2 3 4 5 7 70 4 6 10

73. Tente fazer sozinho
13- Reduza as frações a um mesmo denominador.
1 1 1 1 3 19 3 5 7
a) , e b) , e c) , e
2 3 4 5 7 70 4 6 10
Respostas:
a) mmc (2,3,4) = 12
b) mmc (5,7,70) = 70
c) mmc (4,6,10) = 60
6 4 3 14 30 19 15 50 32
a) , e b) , e c) , e
12 12 12 70 70 70 60 60 60

74. Compar ação de
Frações
 Para comparar frações com numeradores e
denominadores diferentes, devemos primeiramente
reduzi-las ao mesmo denominador.
 Vamos comparar 7/8 e 5/6.
mmc (8, 6) = 24
5 20 7 21
Então: = =
6 24 8 24
20 21
Agora comparamos: <
24 24
5 7
Portanto: <
6 8

75. Resumindo
O que é divisão
numerador
termos
denominador
própria n<d
tipos imprópria n>d Número Misto
Fração
aparente n:d
Frações Equivalentes
Reduzir 1o mmc dos denominadores
ao mesmo 2o dividir o mmc pelo denominador
denominador e multiplicar pelo numerador
1o reduzir ao mesmo denominador
Comparar
2o localizar o numerador maior

76. Tente fazer so zinho
14- Faça a comparação entre as frações
utilizando >, < e =.
2 2 1 2 2 3 11 4
a ) ___ b) ___ c) ___ d ) ___
5 7 7 14 9 7 4 3

77. Tente fazer so zinho
14- Faça a comparação entre as frações
utilizando >, < e =.
2 2 1 2 2 3 11 4
a ) ___ b) ___ c) ___ d ) ___
5 7 7 14 9 7 4 3

78. Tente fazer so zinho
14- Faça a comparação entre as frações
utilizando >, < e =.
2 2 1 2 2 3 11 4
a ) ___ b) ___ c) ___ d ) ___
5 7 7 14 9 7 4 3
Respostas:
a) mmc (5,7) = 35 b) mmc (7,14) = 14
c) mmc (7,9) = 63 d) mmc (3,4) = 12
14 10 2 2 14 27 33 16
a) > b) = c) < d) >
35 35 14 14 63 63 12 12

79. Oper ações com
Fr ações
 Soma
 Subtração
 Multiplicação
 Divisão
 Potenciação

80. Resumindo
O que é divisão
numerador
termos
denominador
própria n<d
tipos imprópria n>d Número Misto
Fração
aparente n:d
Frações Equivalentes
Reduzir 1o mmc dos denominadores
ao mesmo 2o dividir o mmc pelo denominador
denominador e multiplicar pelo numerador
1o reduzir ao mesmo denominador
Comparar
2o localizar o numerador maior
Operações

81. Oper ações com Fr ações
- Soma -
Temos 3 copos iguais, com uma graduação dividida
em 7 partes.
Vamos preencher com água 2/7 do copo 1 e 3/7 do
copo 2. O terceiro continuará vazio.
Se despejarmos a água dos copos 1 e 2 no copo 3,
teremos nesse copo 5/7.
Somamos
2 3 5
+ =
7 7 7

82. Oper ações com Fr ações
- Subtr ação -
Temos um retângulo, vamos dividi-lo em 11 partes
iguais e pintar 8 dessas partes.
Vamos retirar a cor de 5 partes pintadas.
Ainda sobrarão 3 partes coloridas. Subtraímos
8 5 3
− =
11 11 11

83. E se os
denominadores for em
difer entes?
 Vamos calcular 4 5
+ .
9 6
 Reduzir as frações ao mesmo denominador.
mmc (9,6) = 18 4 8 5 15
= =
9 18 6 18
 Agora podemos somar.
4 5 8 15 23
+ = + =
9 6 18 18 18
 Assim fazemos para soma e subtração de frações.

84. Resumindo
soma
1o Igualar denominadores
2o Somar ou Subtrair
subtração
Operações

85. Tente fazer so zinho
15- Some as frações de cada lado e descubra quem
vai ganhar a guerra da corda. Ganha quem tiver a
maior soma.

86. Tente fazer sozinho
15- Some as frações de cada lado e descubra quem
vai ganhar a guerra da corda. Ganha quem tiver a
maior soma.

87. Resposta:
5 5.7 5 35 5 40
5 = + = + =
7 7 7 7 7 7 1 2
1+ + =
2 4.7 2 28 2 30 3 3
4 = + = + =
7 7 7 7 7 7 3 1 2 6
40 30 + + = =2
+ +1 = 3 3 3 3
7 7
40 30 7 77
+ + = = 11
7 7 7 7

88. Tente fazer so zinho
16- Carla está lendo um livro. Anteontem ela leu 1/4 do
livro e ontem 1/3, mas ainda faltam 30 páginas.
Qual é o número de páginas desse livro?

89. Tente fazer so zinho
16- Carla está lendo um livro. Anteontem ela leu 1/4 do
livro e ontem 1/3, mas ainda faltam 30 páginas.
Qual é o número de páginas desse livro?

90. Tente fazer so zinho
16- Carla está lendo um livro. Anteontem ela leu 1/4 do
livro e ontem 1/3, mas ainda faltam 30 páginas.
Qual é o número de páginas desse livro?
Resposta:
1 1 3 4 7 O que ela leu.
+ = + =
4 3 12 12 12
12 7 5
− = Total do livro – o que ela leu = o que falta ler.
12 12 12
O que falta ler = 30 páginas
5 30
=
12 Buscar uma fração equivalente com numerador 30,
x6 então multiplicamos por 6.
5 30
=
12 x 6 72 Encontramos 72 de denominador que é o número
total de páginas do livro.

91. Oper ações com Fr ações
- Multiplicação -
 2/7 do retângulo é a parte colorida da
figura.
Quanto é
3 x 2/7 ?
 Assim 3 x 2/7 é o triplo dessa parte.
Multiplicamos
2 3.2 6
3. = =
7 7 7

92. E se os dois fator es
for em fr ações?
1 1
 Vamos calcular x .
3 5
 1/5 do retângulo é a parte colorida.
 Notamos que 1/3 x 1/5 é 1/3 da parte colorida, que
corresponde a 1/15.
Multiplicamos
1 1 1.1 1
. = =
3 5 3.5 15

93. Resumindo
soma
1o Igualar denominadores
2o Somar ou Subtrair
subtração
numerador x numerador
Operações multiplicação
denominador x denominador

94. Tente fazer so zinho
17- Que fração representa a parte colorida da figura?
Agora calcule:
 O dobro dessa fração
 O triplo dessa fração
 A metade dessa fração
 A terça parte dessa fração
 2/3 dessa fração
 5/8 dessa fração

95. Tente fazer so zinho
17- Que fração representa a parte colorida da figura?
Agora calcule:
 O dobro dessa fração
 O triplo dessa fração
 A metade dessa fração
 A terça parte dessa fração
 2/3 dessa fração
 5/8 dessa fração

96. Tente fazer so zinho
17- Que fração representa a parte colorida da figura?
1
Agora calcule:
Respostas: 5
1 2.1 2
 O dobro dessa fração a ) 2. = =
5 5 5
1 3.1 3
 O triplo dessa fração b)3. = =
5 5 5
1 1 1.1 1
 A metade dessa fração c) . = =
2 5 2.5 10
1 1 1.1 1
 d) . = =
A terça parte dessa fração 3 5 3.5 15
2 1 2.1 2
e) . = =
 2/3 dessa fração 3 5 3.5 15
÷5
5 1 5.1 5 1
 5/8 dessa fração f) . = = =
8 5 8.5 40 ÷5 8

97. Tente fazer so zinho
18- Resolva a equação:
1 5 2 5 2
1 + . − . −  =
2 4 3 2 5

98. Tente fazer so zinho
18- Resolva a equação:
1 5 2 5 2
1 + . − . −  =
2 4 3 2 5

99. Tente fazer sozinho
18- Resolva a equação: Resposta:
1 5 2 5 2 5 2  25 4 
1 + . − . −  = 1 + − . −  =
2 4 3 2 5 8 3  10 10 
5 2 21
1+ − . =
8 3 10
5 1 7
1+ − . =
8 1 5
5 7
1+ − =
8 5
40 25 56 9
+ − =
40 40 40 40

100. Oper ações com Fr ações
- Divisão -
 Desejamos dividir 40 litros de leite em canecas de
½ litro cada uma. Quantas canecas serão
necessárias?
 Como fazer: Dividimos
1o Repete a 1a fração 1 2
40 ÷ = 40. =
2o Inverter a 2a fração 2 1
40.2 80
3o Multiplicamos = = 80
1 1

101. E se os dois fator es
for em fr ações?
 Se quisermos dividir 1/2 litro de leite em 4 copos.
 Procedemos da mesma maneira:
1o Repete a 1a fração
2o Inverter a 2a fração
3o Multiplicamos
Dividimos
1 1 1
÷4 = . =
2 2 4
1 .1 1
=
2 .4 8

102. Resumindo
soma
1o Igualar denominadores
2o Somar ou Subtrair
subtração
numerador x numerador
Operações multiplicação
denominador x denominador
1o Repete a 1a fração
divisão
2o Multiplica pelo inverso da 2a fração

103. Tente fazer so zinho
19- A divisão dos inversos dos números 3 e 3/7 é igual a :

104. Tente fazer so zinho
19- A divisão dos inversos dos números 3 e 3/7 é igual a :

105. Tente fazer so zinho
19- A divisão dos inversos dos números 3 e 3/7 é igual a :
Resposta:
1
3− > inverso− >
3
3 7
− > inverso− >
7 3
1 7 1 3 1
÷ = . =
3 3 3 7 7

106. Tente fazer so zinho
20- Calcule:
4 2
:
15 3 =
12 3
:
24 8

107. Tente fazer so zinho
Resposta:
20- Calcule:
4 2 4 3 2 1 2
: . .
15 3 = 15 2 = 5 1 = 5 = 2 . 3 = 1 . 3 = 3
12 3 12 8 4 1 4 5 4 5 2 10
: . .
24 8 24 3 3 1 3

108. Oper ações com Fr ações
- Potenciação -
 Observe o cálculo de algumas potências:
4
2  24 16  Como fazer:
  = 4 =
3  3 81
Elevar numerador
1
e denominador à
2  21 2 mesma potência.
  = 1 =
3  3 3
0
 2 20 1
  = 0 = =1
3  3 1

109. Resumindo
soma
1o Igualar denominadores
2o Somar ou Subtrair
subtração
numerador x numerador
Operações multiplicação
denominador x denominador
1o Repete a 1a fração
divisão
2o Multiplica pelo inverso da 2a fração
Eleva numerador e denominador
potenciação
à mesma potencia

110. Tente fazer so zinho
21- Calcule o valor da expressão:
2 3 5
2 2 2
  .  :  =
3 3 3

111. Tente fazer so zinho
21- Calcule o valor da expressão:
2 3 5
2 2 2
  .  :  =
3 3 3

112. Tente fazer so zinho
21- Calcule o valor da expressão:
Resposta:
2 3 5
2 2 2  2  2   2 
2 3 5
  .  :  =  2 . 3  :  5  =
3 3 3  3  3   3 
    
4 8 32
. : =
9 27 243
32 32
: =
243 243
32 243 1 1
. = . =1
243 32 1 1

113. Tente fazer so zinho
22- Calcule:
3
1 1
 −  =
2 6

114. Tente fazer so zinho
22- Calcule:
3
1 1
 −  =
2 6

115. Tente fazer so zinho
22- Calcule:
3
1 1
 −  =
2 6
Resposta:
3
3 1
 −  =
6 6
3 3
 2   1  13 1
  =  = 3 =
 6 3 3 27

116. O que você
aprendeu
 O que é fração
 Tipos de fração
 Número misto
 Frações equivalentes
 Simplificação de frações
 Comparação de frações
 Operações com frações
 Potenciação de frações

117. Bibliog r afia
 Matemática e Realidade – ensino
fundamental, 6o ano. IEZZI, Gelson, DOLCE,
Osvaldo, MACHADO, Antonio. 2005, São
Paulo. Páginas pesquisadas: 152 a 196.
 Site: Só Matemática, acessado em 11/12/10
http://www.somatematica.com.br/soexercicios/frac