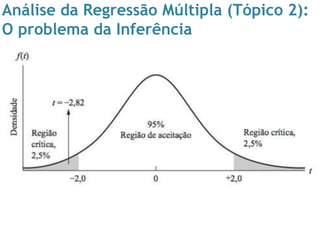
1) O documento discute o problema da inferência na regressão múltipla, incluindo testes de hipóteses sobre os coeficientes e o uso da estatística F.
2) É mostrado um exemplo com dados de mortalidade infantil, onde os coeficientes são testados individualmente usando o teste t e conjuntamente usando o teste F.
3) A análise da contribuição incremental de cada variável é discutida por meio da decomposição da soma dos quadrados do modelo.