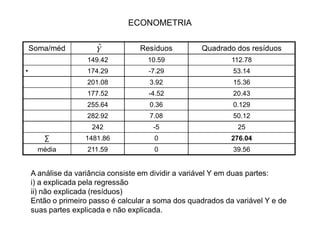
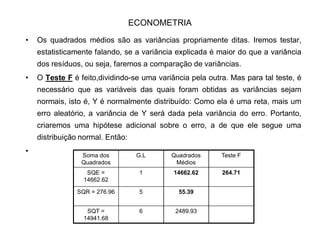
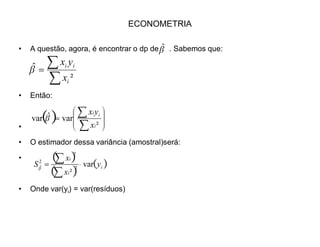
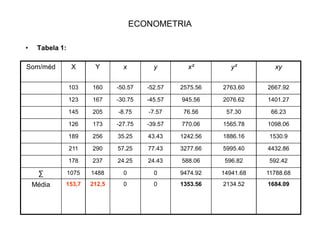
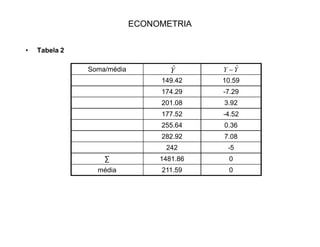
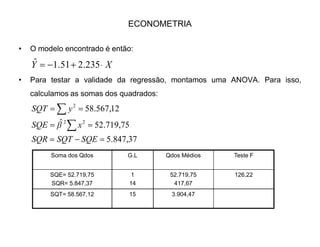
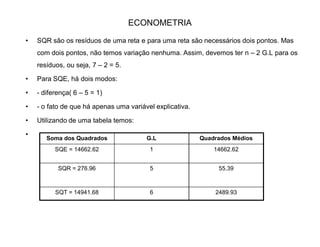
1) O documento descreve um modelo de regressão linear simples, apresentando a equação, o método dos mínimos quadrados ordinários para estimar os parâmetros, e os testes de significância dos parâmetros e da regressão como um todo. 2) É apresentado um exemplo numérico ilustrando os cálculos para estimar a reta de regressão e os testes. 3) A regressão é validada através dos testes F e t, indicando que os parâmetros são estatisticamente significativos.

1. ECONOMETRIA 1
MODELO DE REGRESSÃO
LINEAR SIMPLES

2. ECONOMETRIA
‡ REFERÊNCIAS:
‡ Introdução à Econometria ± Uma abordagem Moderna.
Jeffrey M. Wooldridge 2ª edição ± 2006
‡ Estatística e Introdução a Econometria ± Alexandre Sartoris ± Ed.Saraiva.
1ªedição - 2004

3. ECONOMETRIA
‡ Regressão: Processo o qual tenta se estimar a relação entre duas ou mais
variáveis
‡ Regressão Linear Simples: ocorre quando a regressão apresenta apenas
uma variável independente.

4. ECONOMETRIA
‡ Regressão Linear Simples(RLS)
‡ Formalmente a RLS se apresenta no seguinte formato:
‡ Sendo:
‡ equação da reta.
‡ : termo de erro.
‡ O termo , deve ser incluído na regressão, pois como mostra o gráfico, o
valor de Y não será exatamente dado pelo ponto da reta. Em segundo, o
termo , se refere diretamente a imprecisão de medidas, por mais preciso
que este seja.
iii exY ! FE
ixFE
ie
ie
ie
y
y
y
y
y
y
y
y
y
y
iY
y
y
ix
y
y
y y
y
y
y
y
y
y y
y
y

5. ECONOMETRIA
‡ Por fim, o erro da conta de todos os eventos de difíceis mensuração, mas
que são (supostamente) aleatórios. Se o modelo que estivermos trabalhando
estiver corretamente especificado, podemos supor, que em média o erro tem
valor zero, isto é, a probabilidade do erro ser x unidades acima da reta é a
mesma de ser x unidades abaixo da reta.
‡ Com isso, temos a primeira hipótese sobre o modelo de regressão:
‡ 1. , os erros tem média zero.

6. 0!ieE

7. ECONOMETRIA
‡ Método dos Mínimos Quadrados Ordinários (OLS)
‡ Estimar a reta de regressão significa na verdade, encontrar os
estimadores para Į e ȕ (pois estamos trabalhando com uma
amostra). Para isso, podemos reordenar as variáveis x e y da
seguinte forma:
‡ x e y são variáveis centradas na média.
Xx '!
Yy 9!

8. ECONOMETRIA
‡ Assim:
‡ (1)
‡ Como por hipótese
‡ (2)
‡ Ao subtrairmos (2) de (1):
‡ Logo:
‡ (3)
‡ Tal metodologia pressupõe que queremos estimar uma reta que tenha o menor
erro possível. Mas somar erros não acrescenta muito, pois há erros negativos e
positivos, que irão se cancelar.

9. 0!ieE
iii eXY ! FE
0! XY FE
iii eXXYY ! )()( FEE
iexy ! F

10. ECONOMETRIA
‡ Para resolvermos isto, basta elevarmos ao quadrado, eliminando os
negativos. Então a melhor reta será aquela cuja a soma dos quadrados dos
erros for mínima. Daí: MQO ou OLS (ordinary least squares).
‡ De (3), usando as variáveis centradas na média:
‡ A soma dos quadrados dos erros:
‡ ou;
‡ Pelas propriedades da soma e como ȕ é uma constante:
xye F!
)²()²(
11
§§ !!
!
n
i
n
i
i xye F )2²²()²(
1
2
1
yxxye
n
i
n
i
i §§ !!
! FF
§ §§§ ! !!!
!
n
i
n
i
n
i
n
i
i xyxye
1 111
2²²²)²( FF

11. ECONOMETRIA
‡ Para Encontrar o valor de ȕ que dê o minimize essa soma, o procedimento é
derivar e igualar a zero. Como o valor de ȕ é um estimador, utilizaremos logo
. .
‡ Derivando em relação a ȕ e igualando a zero:
‡ Dividindo por dois em ambos os lados:
‡ Assim :
‡ (4)
FÖ
§ § ! 02²Ö2 xyxF
0²Ö !§ §xyxF
0
²
Ö !!
§
§
x
xy
F

12. ECONOMETRIA
‡ E o estimador para :
‡ Substituindo pelos respectivos estimadores:
‡
‡ portanto:
‡ (5)
E
XY FE !
XY FE ÖÖ !
XY FE ÖÖ !

13. ECONOMETRIA
‡ Tabela 1:
Som/méd X Y x y x² y² xy
103 160 -50.57 -52.57 2575.56 2763.60 2667.92
123 167 -30.75 -45.57 945.56 2076.62 1401.27
145 205 -8.75 -7.57 76.56 57.30 66.23
126 173 -27.75 -39.57 770.06 1565.78 1098.06
189 256 35.25 43.43 1242.56 1886.16 1530.9
211 290 57.25 77.43 3277.66 5995.40 4432.86
178 237 24.25 24.43 588.06 596.82 592.42
™ 1075 1488 0 0 9474.92 14941.68 11788.68
Média 153,7 212,5 0 0 1353.56 2134.52 1684.09

14. ECONOMETRIA
‡ Agora podemos facilmente estimar a reta de regressão que na
tabela representa os valores em negrito:
‡ = 1684.09 /1353.56 = 1.244
‡ E para o intercepto, utilizamos os valores em vermelho:
‡ = 212.57 ± 1.244 x 153.75 = 21.28
‡ A reta a ser estimada é dada por:
‡ = 21.28 + 1.244.
‡ Significando que se x = 150:
‡ = 21.28 + 1.244. 150 = 207.88
FÖ
XY FE ÖÖ !
YÖ XÖ
YÖ

15. ECONOMETRIA
‡ Devemos verificar se a regressão é boa e a maneira mais formal é calcular
a diferença entre os dados no exemplo e o da reta de regressão:
‡ = 21.28 + 1.244. 103 = 149.42
‡ = 21.28 + 1.244. 123 = 174.29
‡ = 21.28 + 1.244. 145 = 201.08
‡ = 177.52
‡ = 255.64
‡ = 282.92
‡ = 242.71
2ÖY
1ÖY
3ÖY
4ÖY
5ÖY
6ÖY
7ÖY

16. ECONOMETRIA
‡ Tabela 2
Soma/média
149.42 10.59
174.29 -7.29
201.08 3.92
177.52 -4.52
255.64 0.36
282.92 7.08
242 -5
™ 1481.86 0
média 211.59 0
YÖ YY Ö

17. ECONOMETRIA
‡ Essas diferenças não são os erros, é quase isso. Os erros são as diferenças
entre os valores de Y e a reta verdadeira, isto é, a reta oriunda de valores
populacionais de e (que não são conhecidos).
‡ As diferenças que encontramos são entre os valores de Y e os dados com os
valores amostrais de e . São, portanto, não os erros, mas os
estimadores dos erros, ou simplesmente os resíduos da regressão.
‡ Analisaremos, agora o quadro dos resíduos e sua variância, a análise da
variância é conhecido como ANOVA.
F
FE
E

18. ECONOMETRIA
‡
Soma/méd Resíduos Quadrado dos resíduos
149.42 10.59 112.78
174.29 -7.29 53.14
201.08 3.92 15.36
177.52 -4.52 20.43
255.64 0.36 0.129
282.92 7.08 50.12
242 -5 25
™ 1481.86 0 276.04
média 211.59 0 39.56
YÖ
A análise da variância consiste em dividir a variável Y em duas partes:
i) a explicada pela regressão
ii) não explicada (resíduos)
Então o primeiro passo é calcular a soma dos quadrados da variável Y e de
suas partes explicada e não explicada.

19. ECONOMETRIA
‡ Calculamos, logo:
‡ 1) SQT Soma dos Quadrados Totais de Y(centrado);
‡ 2) SQE Soma dos Quadrados Explicativos (Y estimado);
‡ 3) SQR Soma dos Quadrados dos Resíduos.
‡ Com tais informações, já é possível tirar uma conclusão a respeito da
regressão, dado que SQR é uma parcela pequena do total ou podemos dizer
que SQE tem uma parcela importante.
‡

20. ECONOMETRIA
‡ SQT = 14941.68 = ™y².
‡ Para a SQE há duas maneiras:
‡ 1 ± Calcular um a um tirando a média e elevando ao quadrado.
‡ 2 ± Ou usarmos a equação da reta:
‡ SQE =
‡ = 1.244² . 9474.92 = 14662.62
‡ e SQR que já foi calculado:
‡ SQR = 276.92
‡ Notando que: SQT = SQR + SQE = 14662.62 + 276.96 = 14941.68
iXY FÖÖ !
iXY FÖÖ !
§§ § !! ²²Ö)²Ö()²Ö( ii XXY FF

21. ECONOMETRIA
‡ Essa proporção é conhecida como poder explicativo, coeficiente de
determinação ou simplesmente R²:
‡ R² = SQE/ SQT = 14665.62/ 14941.68 = 0.9814 = 98.14%
‡ Note que é impossível SQE SQT e este também não pode ser negativo. Logo
0 ” R² ” 1.
‡ Como R² = 98.14%, dizemos que 98.14% da variância de Y é explicada por X,
indicando que a regressão de Y por X indicou um bom resultado.
‡

22. ECONOMETRIA
‡ Contudo, a análise continua. Colocaremos os Graus de Liberdade(G.L)
‡ ( lembrando que G.L é adquirido através da variância amostral que é dada
por porque seu estimador é uma soma de n ± 1
variáveis normais padronizadas, dado que S² é obtido de uma variável cuja a
distribuição é normal.). Para SQT, os Graus de Liberdade são os mesmos p/
variância amostral normal, ou seja, 7 ± 1 = 6.
1/²)(²
1
!§!
nXXS
n
i

23. ECONOMETRIA
‡ SQR são os resíduos de uma reta e para uma reta são necessários dois pontos. Mas
com dois pontos, não temos variação nenhuma. Assim, devemos ter n ± 2 G.L para os
resíduos, ou seja, 7 ± 2 = 5.
‡ Para SQE, há dois modos:
‡ - diferença( 6 ± 5 = 1)
‡ - o fato de que há apenas uma variável explicativa.
‡ Utilizando de uma tabela temos:
‡
Soma dos Quadrados G.L Quadrados Médios
SQE = 14662.62 1 14662.62
SQR = 276.96 5 55.39
SQT = 14941.68 6 2489.93

24. ECONOMETRIA
‡ Os quadrados médios são as variâncias propriamente ditas. Iremos testar,
estatisticamente falando, se a variância explicada é maior do que a variância
dos resíduos, ou seja, faremos a comparação de variâncias.
‡ O Teste F é feito,dividindo-se uma variância pela outra. Mas para tal teste, é
necessário que as variáveis das quais foram obtidas as variâncias sejam
normais, isto é, Y é normalmente distribuído: Como ela é uma reta, mais um
erro aleatório, a variância de Y será dada pela variância do erro. Portanto,
criaremos uma hipótese adicional sobre o erro, a de que ele segue uma
distribuição normal. Então:
‡
Soma dos
Quadrados
G.L Quadrados
Médios
Teste F
SQE =
14662.62
1 14662.62 264.71
SQR = 276.96 5 55.39
SQT =
14941.68
6 2489.93

25. ECONOMETRIA
‡ Consultando a Tabela de distribuição F, acharemos o valor limite da distribuição
para o teste, com 1 G.L para o numerador e 5 para o denominador, a 5% de
significância:
‡ F1,5 = 6.61 FTABELADO
‡ FCALCULADO = 264.71
‡ Logo Fc FT. Na regressão, temos a hipótese nula de que as variâncias são
iguais. Se rejeitarmos H0, isso significa que a regressão explica mais do que
não explica, considerando a regressão válida. No nosso caso, Fc FT, por isso
a regressão é valida a 5% de significância.

26. ECONOMETRIA
‡ Teste de Significância dos Parâmetros.
‡ Testar a significância dos parâmetros significa testar H0 de que e são, na
verdade, iguais a zero. Isto é, será que os parâmetros não existem de fato, e o
valor que encontramos é apenas resultados da amostra?
‡ Isto equivale a testar as seguintes hipóteses p/ (assim como p/ ):
E F
F E
0:
0:
1
0
{
!
F
F
H
H

27. ECONOMETRIA
‡ Como são variáveis normalmente distribuídas, cuja a variância não
conhecemos ao certo, a distribuição a ser utilizada é a t de Student. Os valores
tabelados com 5 (= n -2) G.L, com 1%, 5% e 10% (bicaudais) são:
‡ E o valor calculado da estatística t é dado por:
‡ Isto é, basta dividir o coeficiente encontrado pelo seu desvio padrão.

30. 032,4
570,2
015,2
%1,5
%5,5
%10,5
!
!
!
t
t
t
FF
FF
ÖÖ
Ö0Ö
SS
!

31. ECONOMETRIA
‡ A questão, agora, é encontrar o dp de . Sabemos que:
‡ Então:
‡
‡ O estimador dessa variância (amostral)será:
‡
‡ Onde var(yi) = var(resíduos)
FÖ

32. ¹
¹
º
¸
©
©
ª
¨
!
§
§
²
varÖvar
i
ii
x
yx
F

35. i
i
i
y
x
x
S var
²
2
2
2
Ö ™!
§
§
F
§
§!
²
Ö
i
ii
x
yx
F

36. ECONOMETRIA
‡ Já que a variância de Y dado X, ou seja, a variância de Y no modelo de
regressão, é a própria variância dos resíduos, que já calculamos na ANOVA é
igual a 55,39 e foi obtida por meio da expressão SQR/(n-2):
‡ O cálculo da estatística é, então:
‡ Como o valor calculado é superior aos tabelados, rejeitamos H0 de que .
‡ Dizemos então que é estatisticamente diferente de zero ou significante a 1%.
28,16
0764,0
244,1Ö
0764,000584,0
92,9474
39,55
Ö
Ö
2
Ö
!!
! !!
F
FF
F
S
SS

38. resíduos
x
nSQR
S
i
var
2/
2
2
Ö
§
!F
0!F
F

39. ECONOMETRIA
‡ O Procedimento para é quase o mesmo. A diferença está no cálculo de seu
desvio padrão. Sabemos que:
‡ Cujo o estimador será dado por:
‡ Logo também é estatisticamente
significante a 1%
E